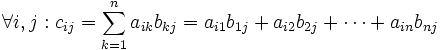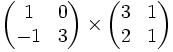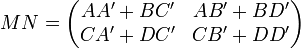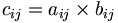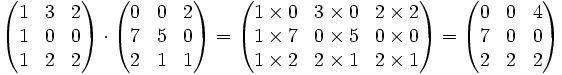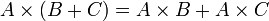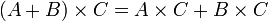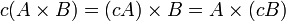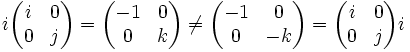Multiplication matricielle

Produit matriciel

Le produit matriciel désigne le produit de matrices, initialement appelé la « composition des tableaux »^[1]. Cet article montre comment multiplier les matrices.

Sommaire

1 Produit matriciel ordinaire
- 1.1 Exemple
2 Multiplication de matrices par bloc
3 Produit d'Hadamard
4 Produit de Kronecker
5 Propriétés communes
6 Multiplication par un scalaire
7 Voir aussi

Produit matriciel ordinaire

Il s'agit de la façon la plus fréquente de multiplier des matrices entre elles. Le produit de deux matrices ne peut se définir que si le nombre de colonnes de la première matrice est le même que le nombre de lignes de la deuxième matrice, c'est-à-dire lorsqu'elles sont de type compatible.

Si $A = (a i j)$ est une matrice de type $(m, n)$ et $B = (b i j)$ est une matrice de type $(n, p)$ , alors leur produit, noté $A B = (c i j)$ est une matrice de type $(m, p)$ donnée par :

$\forall i, j : c_{ij} = \sum_{k=1}^n a_{ik}b_{kj} = a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+ a_{in}b_{nj}$

La figure suivante montre comment calculer les coefficients $c 12$ et $c 33$ de la matrice produit $A B$ si $A$ est une matrice de type $(3,2)$ , et $B$ est une matrice de type $(2,3)$ .

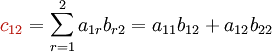
${\color{BrickRed}c_{12}} = \sum_{r=1}^2 a_{1r}b_{r2} = a_{11}b_{12}+a_{12}b_{22}$

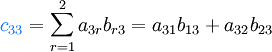
${\color{NavyBlue}c_{33}} = \sum_{r=1}^2 a_{3r}b_{r3} = a_{31}b_{13}+a_{32}b_{23}$

Exemple

$\begin{pmatrix} 1 & 0 \\ -1 & 3 \end{pmatrix} \times \begin{pmatrix} 3 & 1 \\ 2 & 1 \\ \end{pmatrix}$

$= \begin{pmatrix} (1 \times 3+0 \times 2) & (1 \times 1+0 \times 1) \\ (-1 \times 3+3 \times 2) & (-1 \times 1+3 \times 1) \end{pmatrix} = \begin{pmatrix} 3 & 1 \\ 3 & 2 \end{pmatrix}$

Cette notion de multiplication est importante parce que si $A$ et $B$ sont interprétées comme des matrices d'applications linéaires (ce qui est presque toujours le cas), alors la matrice produit $A B$ représente la matrice de la composition des deux applications linéaires, avec celle qui correspond à $B$ qui est appliquée en premier.

En général, la multiplication des matrices n'est pas commutative, c'est-à-dire que $A B$ n'est pas égal à $B A$ .

Multiplication de matrices par bloc

Si l'on considère les matrices 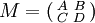$M = \left(\begin{smallmatrix} A & B \\ C & D \end{smallmatrix}\right)$ et $N = \left(\begin{smallmatrix} A' & B' \\ C' & D' \end{smallmatrix}\right)$ , où $A, A', B, B', C, C'$ et $D, D'$ sont des matrices vérifiant :

Le nombre de colonnes de $A$ et $C$ est égal au nombre de lignes de $A'$ et $B'$
Le nombre de colonnes de $B$ et $D$ est égal au nombre de lignes de $C'$ et $D'$

on a alors l'égalité

$M N = \begin{pmatrix} A A' + B C'& A B' + B D' \\ C A' + D C' & C B' + D D' \end{pmatrix}$

On remarquera l'analogie entre le produit de matrice par blocs et le produit de deux matrices carrées d'ordre 2.

N.B. : On ne définit pas ainsi une nouvelle forme de multiplication de matrices. Cela correspond simplement à une méthode de calcul du produit matriciel ordinaire pouvant simplifier les calculs.

Produit d'Hadamard

Pour deux matrices de même type, nous avons le produit d'Hadamard ou produit composante par composante. Le produit d'Hadamard de deux matrices $A = (a i j)$ et $B = (b i j)$ de type $(m, n)$ , noté $A \cdot B = (c ij)$ , est une matrice de type $(m, n)$ donnée par

$c_{ij}=a_{ij}\times b_{ij}$

Par exemple :

$\begin{pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 & 2 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 1 \times 0 & 3 \times 0 & 2 \times 2 \\ 1 \times 7 & 0 \times 5 & 0 \times 0 \\ 1 \times 2 & 2 \times 1 & 2 \times 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 4 \\ 7 & 0 & 0 \\ 2 & 2 & 2 \end{pmatrix}$

Remarquons que le produit d'Hadamard est une sous-matrice du produit de Kronecker (voir ci-dessous). Le produit d'Hadamard est étudié par les théoriciens des matrices, mais n'est pas du tout utilisé par les algébristes linéaires.

Produit de Kronecker

Article détaillé : Produit de Kronecker.

Pour deux matrices arbitraires $A = (a i j)$ et $B$ , nous avons le produit tensoriel ou produit de Kronecker $A \otimes B$ qui est défini par

$\begin{pmatrix} a_{11}B & a_{12}B & \cdots & a_{1n}B \\ \vdots & \vdots & \cdots & \vdots \\ a_{n1}B & a_{n2}B & \cdots & a_{mn}B \end{pmatrix}$

Remarquons que si $A$ est une matrice de type $(m, n)$ et $B$ est une matrice de type $(p, r)$ alors $A \otimes B$ est une matrice de type $(m p, n r)$ . À nouveau cette multiplication n'est pas commutative.

Par exemple

$\begin{pmatrix} 1 & 2 \\ 3 & 1 \\ \end{pmatrix} \otimes \begin{pmatrix} 0 & 3 \\ 2 & 1 \\ \end{pmatrix} = \begin{pmatrix} 1\times 0 & 1\times 3 & 2\times 0 & 2\times 3 \\ 1\times 2 & 1\times 1 & 2\times 2 & 2\times 1 \\ 3\times 0 & 3\times 3 & 1\times 0 & 1\times 3 \\ 3\times 2 & 3\times 1 & 1\times 2 & 1\times 1 \\ \end{pmatrix} = \begin{pmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{pmatrix}$ .

Si $A$ et $B$ sont les matrices d'applications linéaires $V 1 \to W 1$ et $V 2 \to W 2$ , respectivement, alors $A \otimes B$ représente le produit tensoriel des deux applications, $V 1 \otimes V 2 \to W 1 \otimes W 2$ .

Propriétés communes

Les trois multiplications matricielles précédentes sont associatives

$A \times (B \times C) = (A \times B) \times C$ ,

distributives par rapport à l'addition :

$A \times (B + C) = A \times B + A \times C$

$(A + B) \times C = A \times C + B \times C$

et compatibles avec la multiplication par un scalaire :

$c(A \times B) = (cA) \times B = A \times (cB)$

Multiplication par un scalaire

La multiplication par un scalaire $r$ d'une matrice $A = (a i j)$ donne le produit

r A = (r a i j)

Si nous travaillons avec des matrices sur un anneau, alors la multiplication par un scalaire est parfois appelée la multiplication à gauche tandis que la multiplication à droite est définie par :

A r = (a i j r)

Quand l'anneau fondamental est commutatif, par exemple, le corps des réels ou des complexes, les deux multiplications sont identiques.

Cependant, si l'anneau n'est pas commutatif, tel que celui des quaternions, alors ils peuvent être différents. Par exemple

$i\begin{pmatrix} i & 0 \\ 0 & j \\ \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & k \\ \end{pmatrix} \ne \begin{pmatrix} -1 & 0 \\ 0 & -k \\ \end{pmatrix} = \begin{pmatrix} i & 0 \\ 0 & j \\ \end{pmatrix}i$

Voir aussi

Notes et références

↑ Alain Connes, Triangle de pensées, Edition Odile Jacob, p.72.

Lien externe

Algorithmes de multiplication
Produit de matrices	Naïf · Strassen · Coppersmith-Winograd
Produit d'entiers	Naïf · Karatsuba · Toom-Cook · Schönhage-Strassen · Fürer

Portail des mathématiques

Ce document provient de « Produit matriciel ».

Catégorie : Matrice

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Multiplication matricielle de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Mécanique matricielle — La mécanique matricielle est une formulation de la mécanique quantique construite par Werner Heisenberg, Max Born, et Pascual Jordan en 1925. La mécanique matricielle est la première définition complète et correcte de la mécanique quantique. Elle … Wikipédia en Français
Fonction matricielle — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Octonion fendu — En mathématiques, les octonions fendus sont une extension non associative des quaternions (ou des quaternions fendus). Ils diffèrent des octonions par la signature de la forme quadratique : les octonions fendus ont une signature de fente… … Wikipédia en Français
Octonion déployé — En mathématiques, les octonions déployés ou octonions fendus sont une extension non associative des quaternions (ou des coquaternions). Ils diffèrent des octonions par la signature de la forme quadratique : les octonions déployés ont une… … Wikipédia en Français
Pseudo-vecteur — Pseudovecteur En physique et en mathématiques, un pseudovecteur ou vecteur axial est un objet mathématique qui se comporte de même manière qu un vecteur pour une rotation directe (conservant les angles orientés), mais qui change de sens lors d… … Wikipédia en Français
Pseudovecteur — Une boucle de courant électrique (noir), crée un flux magnétique (bleu). Si on considère le système en miroir dans lequel le vecteur courant I est réfléchi, alors le pseudovecteur densité de flux magnétique B doit être réfléchi et inversé. En… … Wikipédia en Français
Vecteur axial — Pseudovecteur En physique et en mathématiques, un pseudovecteur ou vecteur axial est un objet mathématique qui se comporte de la même manière qu un vecteur pour une rotation directe (conservant les angles orientés) mais qui change de sens lors d… … Wikipédia en Français
Complexe fendu — Nombre complexe fendu En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres… … Wikipédia en Français
Nombre Complexe Fendu — En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres complexes (usuels) respecte la … Wikipédia en Français
Nombre complexe fendu — En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence clef entre les deux est que la multiplication des nombres complexes (usuels) respecte la … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Multiplication matricielle

Produit matriciel

Sommaire