- Divergence (opérateur)
-
Divergence (mathématiques)
Articles d'analyse vectorielle 
Objets d'étude Champ vectoriel Champ scalaire Équation aux dérivées partielles de Laplace de Poisson Opérateurs Nabla Gradient Rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Théorèmes de Green de Stokes de Helmholtz de flux-divergence du gradient du rotationnel L'opérateur divergence est un opérateur différentiel linéaire aux dérivées partielles premières, souvent utilisé en physique, notamment pour exprimer des lois de conservation. Il transforme un champ vectoriel en un champ scalaire (c’est-à-dire en une fonction de plusieurs variables) et plus généralement un champ tensoriel d'ordre k en un champ d'ordre k − 1.
Sommaire
Divergence d'un champ de vecteurs
En dimension 3 et en coordonnées cartésiennes, on définit la divergence d'un champ de vecteurs
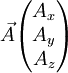 par la relation
par la relation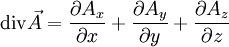
Formellement, l'opérateur divergence appliqué à un champ vectoriel
 est aussi le produit scalaire du vecteur nabla
est aussi le produit scalaire du vecteur nabla  par le vecteur
par le vecteur 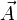 .
.
Il revient au même de dire que
 .
.Ici, le champ
 est considéré comme une application de
est considéré comme une application de  dans lui même, et
dans lui même, et 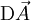 désigne sa différentielle – la matrice jacobienne –, dont on prend la trace.
désigne sa différentielle – la matrice jacobienne –, dont on prend la trace.Cette dernière présentation a l'avantage d'être indépendante du choix de la base. Tout ce qui précède est aussi valable sur
 Exemple :
Exemple :Si
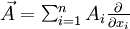 est un champ linéaire, c’est-à-dire si
est un champ linéaire, c’est-à-dire si 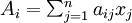 , sa divergence est égale à
, sa divergence est égale à 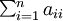 . C'est la trace de la matrice formée par les nombres aij (
. C'est la trace de la matrice formée par les nombres aij (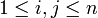 ).
).Interprétation de la divergence
La divergence s'interprète en termes de flux. Si D est un domaine de
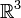 de bord S, le flux de
de bord S, le flux de 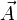 à travers S est égal à l'intégrale sur D de la divergence, d'après le théorème de Stokes.
à travers S est égal à l'intégrale sur D de la divergence, d'après le théorème de Stokes.Une interprétation voisine est la suivante. Soit φt le flot du champ
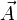 (c’est-à-dire la valeur au temps t de la solution du système différentiel
(c’est-à-dire la valeur au temps t de la solution du système différentiel 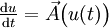 qui vaut x en 0) on a
qui vaut x en 0) on a
(on a désigné par LA l'opérateur dérivée de Lie ; pour les détails et un énoncé plus général, voir opérateur de Laplace-Beltrami).
En particulier, le flot de
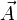 conserve le volume (c’est-à-dire vol(φt(D)) = vol(D) pour tout domaine D) si et seulement si la divergence est partout nulle. Le volume augmente si la divergence est positive, diminue si elle est négative.
conserve le volume (c’est-à-dire vol(φt(D)) = vol(D) pour tout domaine D) si et seulement si la divergence est partout nulle. Le volume augmente si la divergence est positive, diminue si elle est négative.Plus généralement, la divergence rend compte de la variation infinitésimale du volume (ou de la charge électrique) autour d'un point, ce qui explique son intervention dans les équations de la mécanique des fluides ou les équations de Maxwell.
Formulaire commenté
a)
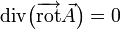
Cette formule est particulière à la dimension 3. Elle signifie qu'un champ rotationnel est à divergence nulle. Inversement, si un champ de vecteurs
 sur un ouvert étoilé de
sur un ouvert étoilé de 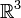 est à divergence nulle, il existe un champ
est à divergence nulle, il existe un champ 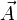 tel que
tel que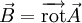
(on dit alors que
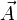 est un potentiel vecteur). Cette propriété, une fois convenablement interprétée en termes de formes différentielles, est une application directe du lemme de Poincaré).
est un potentiel vecteur). Cette propriété, une fois convenablement interprétée en termes de formes différentielles, est une application directe du lemme de Poincaré).Attention. Le champ newtonien
 est à divergence nulle, mais il n'existe pas de champ de vecteurs
est à divergence nulle, mais il n'existe pas de champ de vecteurs 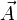 tel que
tel que 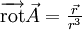 . En effet, si tel était le cas, son flux à travers toute surface fermée serait nul, alors que son flux à travers les sphères centrées à l'origine vaut 4π. En fait, ce champ n'est défini que sur l'espace privé de l'origine, qui n'est pas un ouvert étoilé : le lemme de Poincaré ne s'applique pas.
. En effet, si tel était le cas, son flux à travers toute surface fermée serait nul, alors que son flux à travers les sphères centrées à l'origine vaut 4π. En fait, ce champ n'est défini que sur l'espace privé de l'origine, qui n'est pas un ouvert étoilé : le lemme de Poincaré ne s'applique pas.b)
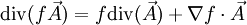
D'après le théorème de Stokes, l'intégrale sur
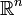 de la divergence d'un champ de vecteurs nul en dehors d'une partie bornée est nulle. Par conséquent, si f est une fonction lisse et
de la divergence d'un champ de vecteurs nul en dehors d'une partie bornée est nulle. Par conséquent, si f est une fonction lisse et 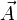 un champ de vecteurs, tous deux nuls en dehors d'une partie bornée (cette condition assurant que les intégrales ont un sens),
un champ de vecteurs, tous deux nuls en dehors d'une partie bornée (cette condition assurant que les intégrales ont un sens), .
.Cette propriété s'interprète de la façon suivante. Soient
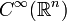 et
et 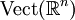 respectivement les espaces vectoriels des fonctions lisses et des champs de vecteurs sur
respectivement les espaces vectoriels des fonctions lisses et des champs de vecteurs sur 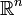 . On les munit des produits scalaires
. On les munit des produits scalaires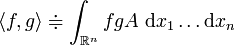 et
et 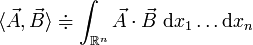
Alors
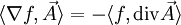 , ce qui permet de voir l'opérateur divergence comme le transposé (au signe près) de l'opérateur gradient.
, ce qui permet de voir l'opérateur divergence comme le transposé (au signe près) de l'opérateur gradient.Cette interprétation de la divergence présente l'avantage de se généraliser aussi bien aux variétés riemanniennes qu'aux tenseurs.
c)
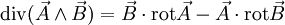
Une application typique de cette formule est le théorème de Poynting en électromagnétisme.
d)

Ces relations, très utilisées en analyse vectorielle, se comprennent mieux dans le cadre des formes différentielles.
Lois de conservation s'exprimant en termes de divergence
- En électromagnétisme, si
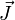 est le vecteur courant et ρ la densité de charge électrique,
est le vecteur courant et ρ la densité de charge électrique,
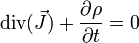 .
.- En mécanique des fluides, si ρ est la masse volumique en un point et
 le champ des vecteurs vitesse,
le champ des vecteurs vitesse,
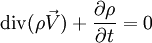 (équation de continuité).
(équation de continuité).- D'autres lois de conservation font intervenir la divergence de tenseurs d'ordre 2, comme la conservation de la quantité de mouvement en mécanique des fluides.
- En relativité générale, la divergence du tenseur énergie-impulsion est nulle.
Divergence d'un tenseur
Cas des espaces euclidiens
Un tenseur de type (p,q) (p-contravariant et q- covariant) est donné par ses coordonnées
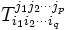 . Sa dérivée covariante est alors par définition le tenseur de type (p,q + 1) donné par
. Sa dérivée covariante est alors par définition le tenseur de type (p,q + 1) donné par 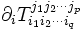 (on a désigné par
(on a désigné par  l'opérateur de dérivation par rapport à la i-ième variable). La divergence est le tenseur de type (p − 1,q) défini par
l'opérateur de dérivation par rapport à la i-ième variable). La divergence est le tenseur de type (p − 1,q) défini par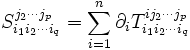 Exemple :
Exemple :La divergence du tenseur
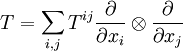
(qui est de type (2,0)) est le champ de vecteurs
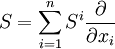 avec
avec 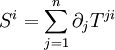
Cas général
Cette définition s'étend pratiquement mot pour mot aux tenseurs sur une variété munie d'une connexion. Dans les formules précédentes, on remplace la différentiation
 par l'opérateur de différentiation covariante
par l'opérateur de différentiation covariante 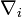 , qui à partir d'un tenseur de type (p,q) donne un tenseur de type (p,q + 1), puis on pose
, qui à partir d'un tenseur de type (p,q) donne un tenseur de type (p,q + 1), puis on pose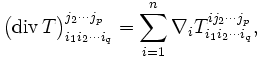
ce qui donne un tenseur de type (p − 1,q)
Le cas le plus important est celui des variétés riemanniennes ou pseudo-riemanniennes, munies de leur connexion de Levi-Civita. La métrique permet d'identifier entre eux les tenseurs de même ordre total p + q. La divergence d'un tenseur d'ordre k sera un tenseur d'ordre k − 1.
Les cas les plus utilisés (avec celui des champs de vecteurs vu plus haut) sont ceux des tenseurs symétriques d'ordre 2 et des formes différentielles.
Bibliographie
- Yvonne Choquet-Bruhat & Cécile deWitt-Morette ; Analysis, Manifolds & Physics - Part I: Basics, North-Holland/Elsevier (2e édition révisée - 1982), ISBN 0-444-86017-7.
- Richard Feynman ; Cours de Physique. Electromagnétisme I, ch. 2 et 3, InterEditions, ISBN 2-72960028-0
- Jacques Lafontaine ; Introduction aux variétés différentielles, Presses Universitaires de Grenoble 1996
- François Rouvière, Petit guide de calcul différentiel à l'usage de la licence et de l'agrégation, Cassini 1999, ISBN 2-84225-008-7
Voir aussi
- Divergence d'un tenseur
- Rotationnel, gradient, nabla, laplacien
- Dérivée partielle, équation aux dérivées partielles
- Opérateur différentiel
- Théorème de Stokes
- Équations de Maxwell, équations de Navier-Stokes
- Portail des mathématiques
- Portail de la physique
Catégories : Analyse vectorielle | Méthode mathématique de la physique - En électromagnétisme, si
Wikimedia Foundation. 2010.
