Divergence D'un Tenseur

Divergence D'un Tenseur

Divergence d'un tenseur

La divergence d'un tenseur est le tenseur obtenu en contractant un des indices de la dérivée covariante avec l'indice de dérivation. Pour une présentation plus générale de l'opérateur de divergence, on se réfèrera à l'article divergence (mathématiques).

Sommaire

Divergence d'un vecteur

Pour un champ vectoriel 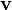\mathbf{v}, on a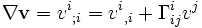

\nabla \mathbf{v} = v^i{}_{;i} = v^i{}_{,i} + \Gamma^i_{ij} v^j

Mettant à profit la formule de contraction

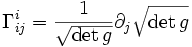\Gamma^i_{ij} = \frac{1}{\sqrt{\det g}}\partial_j \sqrt{\det g},

on a

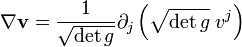\nabla \mathbf{v} = \frac{1}{\sqrt{\det g}} \partial_j \left(\sqrt{\det g} \; v^j \right).

Cette formule permet, une fois établi le tenseur métrique, de calculer facilement la divergence dans un système de coordonnées quelconque.

En coordonnées sphériques

En coordonnées sphériques, la racine carrée du déterminant du tenseur métrique vaut rsinθ et la divergence d'un champ de vecteurs s'écrit

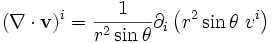(\nabla \cdot \mathbf{v})^i = \frac{1}{r^2 \sin\theta} \partial_i \left(r^2 \sin\theta \; v^i\right).

Dans la base naturelle, on a

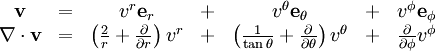
\begin{matrix} \mathbf{v} &=& v^r \mathbf{e}_r &+& v^\theta \mathbf{e}_\theta &+& v^\phi \mathbf{e}_\phi \\ \nabla \cdot \mathbf{v} &=& \left(\frac{2}{r} + \frac{\partial}{\partial r}\right) v^r &+& \left(\frac{1}{\tan\theta} + \frac{\partial}{\partial \theta}\right) v^\theta &+& \frac{\partial}{\partial \phi} v^\phi \end{matrix}

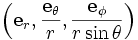et donc dans la base orthonormée \left(\mathbf{e}_r, \frac{\mathbf{e}_{\theta}}{r}, \frac{\mathbf{e}_{\phi}}{r \sin\theta}\right) :

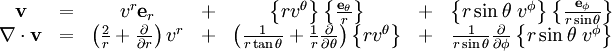
\begin{matrix} \mathbf{v} &=& v^r \mathbf{e}_r &+& \left\{ r v^\theta \right\} \left\{ \frac{\mathbf{e}_\theta}{r} \right\} &+& \left\{ r \sin\theta \; v^\phi \right\} \left\{ \frac{\mathbf{e}_\phi}{r \sin\theta} \right\}\\ \nabla \cdot \mathbf{v} &=& \left(\frac{2}{r} + \frac{\partial}{\partial r}\right) v^r &+& \left( \frac{1}{r \tan \theta} + \frac{1}{r} \frac{\partial}{\partial \theta} \right) \left\{r v^\theta\right\} &+& \frac{1}{r \sin\theta}\frac{\partial}{\partial \phi} \left\{ {r \sin\theta \; v^\phi} \right\} \end{matrix}

En coordonnées cylindriques

En coordonnées cylindriques, la racine carrée du déterminant du tenseur métrique vaut r et la divergence d'un champ de vecteurs s'écrit

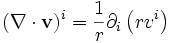(\nabla \cdot \mathbf{v})^i = \frac{1}{r} \partial_i \left(r v^i\right).

Dans la base naturelle, on a

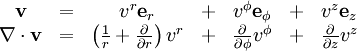
\begin{matrix} \mathbf{v} &=& v^r \mathbf{e}_r &+& v^\phi \mathbf{e}_\phi &+& v^z \mathbf{e}_z \\ \nabla \cdot \mathbf{v} &=& \left(\frac{1}{r} + \frac{\partial}{\partial r}\right) v^r &+& \frac{\partial}{\partial \phi} v^\phi &+& \frac{\partial}{\partial z} v^z \end{matrix}

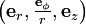et donc dans la base orthonormée \left(\mathbf{e}_r, \tfrac{\mathbf{e}_{\phi}}{r}, \mathbf{e}_{z} \right) :

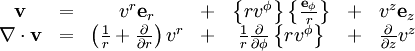
\begin{matrix} \mathbf{v} &=& v^r \mathbf{e}_r &+& \left\{r v^\phi\right\} \left\{\frac{\mathbf{e}_\phi}{r}\right\} &+& v^z \mathbf{e}_z \\ \nabla \cdot \mathbf{v} &=& \left(\frac{1}{r} + \frac{\partial}{\partial r}\right) v^r &+& \frac{1}{r} \frac{\partial}{\partial \phi} \left\{r v^\phi\right\} &+& \frac{\partial}{\partial z} v^z \end{matrix}

Divergence d'un tenseur d'ordre 2

Suivant le même chemin que pour la divergence d'un champ de vecteurs, on écrit

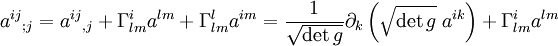
a^{ij}{}_{;j} = a^{ij}{}_{,j} + \Gamma^i_{lm} a^{lm} + \Gamma^l_{lm} a^{im} = \frac{1}{\sqrt{\det g}} \partial_k \left(\sqrt{\det g} \; a^{ik}\right) + \Gamma^i_{lm} a^{lm}

Divergence d'un tenseur antisymétrique d'ordre 2

Dans le cas d'un tenseur antisymétrique, on a

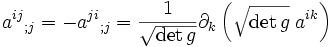
a^{ij}{}_{;j} = -a^{ji}{}_{;j} = \frac{1}{\sqrt{\det g}} \partial_k \left(\sqrt{\det g} \; a^{ik}\right)

En effet, le terme 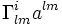\Gamma^i_{lm} a^{lm} est nul puisque

\Gamma^i_{lm} a^{lm} = -\Gamma^i_{lm} a^{ml} = -\Gamma^i_{ml} a^{ml} = -\Gamma^i_{lm} a^{lm}.

Remarques

En écriture quadridimensionnelle, les équations de Maxwell mettent en jeu la divergence du tenseur de champ électromagnétique et de son dual, qui sont des tenseurs antisymétriques d'ordre 2.

Voir aussi

Ce document provient de « Divergence d%27un tenseur ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Divergence D'un Tenseur de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Divergence d'un tenseur — La divergence d un tenseur est le tenseur obtenu en contractant un des indices de la dérivée covariante avec l indice de dérivation. Pour une présentation plus générale de l opérateur de divergence, on se réfèrera à l article divergence… …   Wikipédia en Français

  • Divergence (Mathématiques) — Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (mathematiques) — Divergence (mathématiques) Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (mathématiques) — Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (opérateur) — Divergence (mathématiques) Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (physique) — Divergence (mathématiques) Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (physique)(mathématiques) — Divergence (mathématiques) Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence en physique — Divergence (mathématiques) Pour les articles homonymes, voir Divergence. Articles d analyse vectorielle …   Wikipédia en Français

  • Divergence (analyse vectorielle) — Pour les articles homonymes, voir Divergence. En géométrie, la divergence d un champ de vecteurs X mesure le défaut à ce que son flot préserve une forme volume Ω. La divergence de X, notée div X, est une fonction à valeurs réelles qui mesure la… …   Wikipédia en Français

  • Tenseur — En mathématiques, plus précisément en algèbre multilinéaire et en géométrie différentielle, un tenseur désigne un objet très général, dont la valeur s exprime dans un espace vectoriel. On peut l utiliser entre autres pour représenter des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”