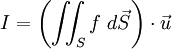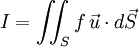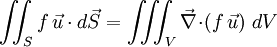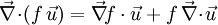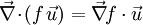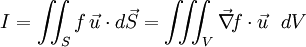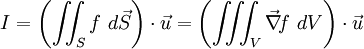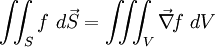Theoreme du gradient
- Theoreme du gradient
-
Théorème du gradient
Le théorème du gradient est un théorème de l'analyse vectorielle qui met en relation l'intégrale de volume du gradient d'un champ scalaire et l'intégrale de surface du même champ.
Le théorème est le suivant :
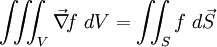 ,
,
où S est le bord de V et f un champ scalaire.
Démonstration
Soit 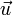 un champ vectoriel uniforme (et non nul).
un champ vectoriel uniforme (et non nul).
Considérons l'intégrale suivante :
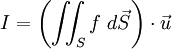
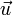 étant uniforme, et le produit scalaire étant commutatif et distributif sur l'addition des vecteurs, on peut écrire :
étant uniforme, et le produit scalaire étant commutatif et distributif sur l'addition des vecteurs, on peut écrire :
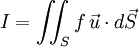
Selon le théorème de flux-divergence,
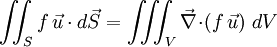
Or, d'après l'une des formules de Leibniz de l'analyse vectorielle,
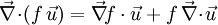
Et puisque la divergence d'un champ vectoriel uniforme est nulle, on a
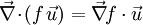
Par conséquent,
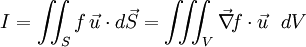
Encore une fois, 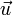 étant uniforme et le produit scalaire commutatif et distributif sur l'addition des vecteurs, on peut écrire :
étant uniforme et le produit scalaire commutatif et distributif sur l'addition des vecteurs, on peut écrire :
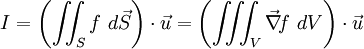
On en déduit donc que
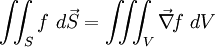
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorème de mathématiques | Analyse vectorielle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme du gradient de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème du gradient — Le théorème du gradient est un théorème de l analyse vectorielle qui met en relation l intégrale de volume du gradient d un champ scalaire et l intégrale de surface du même champ. Le théorème est le suivant : , où S est le bord de V et f un… … Wikipédia en Français
Gradient de pression — Gradient Les lignes bleues représentent le gradient de couleur du plus clair vers le plus foncé En physique, en analyse vectorielle, on définit le gradient comme une grandeur vectorielle qui indique de quelle façon une grandeur physique varie… … Wikipédia en Français
Gradient de température — Gradient Les lignes bleues représentent le gradient de couleur du plus clair vers le plus foncé En physique, en analyse vectorielle, on définit le gradient comme une grandeur vectorielle qui indique de quelle façon une grandeur physique varie… … Wikipédia en Français
Theoreme du rotationnel — Théorème du rotationnel Articles d analyse vectorielle … Wikipédia en Français
Gradient — Les lignes bleues représentent le gradient de couleur du plus clair vers le plus foncé En physique et en analyse vectorielle, on définit le gradient comme une grandeur vectorielle qui indique de quelle façon une grandeur physique varie dans l… … Wikipédia en Français
Théorème du rotationnel — En analyse vectorielle, le théorème du rotationnel est un théorème qui met en relation l intégrale de volume du rotationnel d un champ vectoriel à l intégrale de surface du même champ. Le théorème est le suivant : où S est la frontière de V … Wikipédia en Français
Theoreme des fonctions implicites — Théorème des fonctions implicites En mathématiques, le théorème des fonctions implicites est un résultat de géométrie différentielle. Certaines courbes sont définies par une équation cartésienne, c est à dire la forme f(x, y) = 0,… … Wikipédia en Français
Theoreme de Frobenius — Théorème de Frobenius En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius… … Wikipédia en Français
Théorème de Frobénius — Théorème de Frobenius En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius… … Wikipédia en Français
Théorème de frobenius — En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius peut s exprimer… … Wikipédia en Français

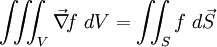 ,
,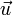 un champ vectoriel uniforme (et non nul).
un champ vectoriel uniforme (et non nul).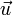 étant uniforme, et le produit scalaire étant commutatif et distributif sur l'addition des vecteurs, on peut écrire :
étant uniforme, et le produit scalaire étant commutatif et distributif sur l'addition des vecteurs, on peut écrire :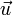 étant uniforme et le produit scalaire commutatif et distributif sur l'addition des vecteurs, on peut écrire :
étant uniforme et le produit scalaire commutatif et distributif sur l'addition des vecteurs, on peut écrire :