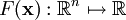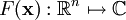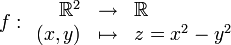Champ Scalaire

Articles d'analyse vectorielle
Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace	de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

Un champ scalaire est une fonction de plusieurs variables qui associe un seul nombre (ou scalaire) à chaque point de l'espace. Les champs scalaires sont souvent utilisés en physique, par exemple pour indiquer la distribution de la température à travers l'espace, ou la pression atmosphérique.

Sommaire 1 Définition 2 Exemple 3 Usage en physique quantique 4 Autres types de champ

Définition

Un champ scalaire est une forme

ou

où x est un vecteur de Rⁿ.

Le champ scalaire peut être visualisé comme un espace à n dimensions avec un nombre complexe ou réel attaché à chaque point de l'espace.

La dérivée d'un champ scalaire résulte en un champ vectoriel appelé le gradient.

Exemple

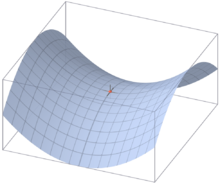
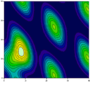
L'image à droite est une représentation graphique du champ scalaire suivant :

Le point en rouge est un point critique de la fonction, point où le gradient s'annule. Il s'agit ici en particulier d'un point selle : il représente un maximum selon une direction et un minimum selon l'autre.

Usage en physique quantique

Dans la théorie quantique des champs, un champ scalaire a pour cause l'échange de particules à spin 0.

Autres types de champ

• Champs vectoriels, qui associent un vecteur à chaque point de l'espace. Quelques exemples de champs vectoriels incluent le champ électromagnétique ou le champ gravitationnel newtonien.

• Champs tensoriels, qui associent un tenseur à chaque point de l'espace. En relativité générale, la gravité est associée à un champ tensoriel. En particulier, est-ce avec le tenseur de courbure riemannien. Dans la théorie de Kaluza-Klein, l'espace-temps est étendu à cinq dimensions et son tenseur de courbure riemannien peut être séparé en la gravitation à quatre dimensions ordinaire et d'un ensemble supplémentaire, qui est équivalent aux équations de Maxwell pour le champ électromagnétique, ainsi qu'un champ scalaire connu sous le nom de « dilaton ».

• Portail des mathématiques