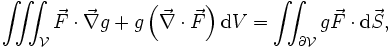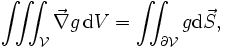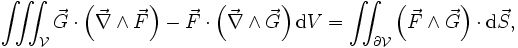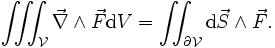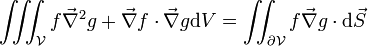Theoreme de flux-divergence

Theoreme de flux-divergence

Théorème de flux-divergence

Articles d'analyse vectorielle
Champ vectorielChamp scalaire
Objets d'étude
Champ vectoriel Champ scalaire
Équation aux dérivées partielles
de Laplace de Poisson
Opérateurs
Nabla Gradient
Rotationnel Divergence
Laplacien scalaire Bilaplacien
Laplacien vectoriel D'alembertien
Théorèmes
de Green de Stokes
de Helmholtz de flux-divergence
du gradient du rotationnel

En analyse vectorielle, le théorème de flux-divergence, aussi appelé le théorème de Green-Ostrogradski est un théorème reliant la divergence d'un champ vectoriel à la valeur de l'intégrale de surface du flux défini par ce champ.

Il énonce que le flux d'un vecteur à travers une surface fermée est égal à l'intégrale de la divergence de ce vecteur sur le volume délimité par cette surface.

L'expression du théorème est la suivante :

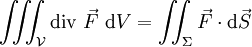
\iiint_{\mathcal{V}} \mathrm{div}\ \vec F \ {\rm d}V = \iint_{\Sigma} \vec F \cdot {\rm d} \vec S

où :

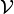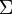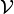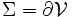\mathcal{V}\, représente le volume, et \Sigma\, le bord de \mathcal{V}\,, ce qu'on note mathématiquement \Sigma=\part\mathcal{V}\,.
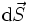{\rm d} \vec S est le vecteur normal à la surface , dirigé vers l'extérieur, et de longueur égale à l'élément qu'il représente .
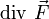\mathrm{div}\ \vec F est aussi noté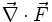 \vec\nabla \cdot \vec F

Ce théorème découle du théorème de Stokes, qui lui-même généralise le théorème fondamental du calcul différentiel et intégral.

C'est un résultat important en physique mathématique, en particulier en électrostatique et en dynamique des fluides.

On peut utiliser ce théorème pour déduire certaines formules utiles de calcul vectoriel :

\iiint_\mathcal{V} \vec{F}\cdot \vec{\nabla} g + g \left(\vec{\nabla} \cdot \vec{F}\right){\rm d}V=\iint_{\part \mathcal{V}}g \vec{F}\cdot {\rm d}\vec{S},
\iiint_\mathcal{V} \vec{\nabla} g \, {\rm d}V=\iint_{\part \mathcal{V}} g {\rm d}\vec{S},
\iiint_\mathcal{V} \vec{G}\cdot\left(\vec{\nabla} \wedge \vec{F}\right) - \vec{F}\cdot \left( \vec{\nabla} \wedge \vec{G}\right) {\rm d}V = \iint_{\part \mathcal{V}}\left(\vec{F} \wedge \vec{G}\right)\cdot {\rm d}\vec{S},
\iiint_\mathcal{V} \vec{\nabla}\wedge \vec{F} {\rm d}V = \iint_{\part \mathcal{V}}{\rm d}\vec{S} \wedge \vec{F}.
\iiint_\mathcal{V} f \vec{\nabla}^{2} g + \vec{\nabla} f \cdot \vec{\nabla} g {\rm d} V = \iint_{\part \mathcal{V}} f \vec{\nabla} g \cdot {\rm d} \vec{S}


Ce thèorème permet notamment de retrouver la version intégrale du théorème de Gauss à partir de l'équation de Maxwell-Gauss :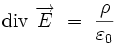

\mathrm{div}\ \overrightarrow{E} \ = \ \frac{\rho}{\varepsilon_0}

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de flux-divergence ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de flux-divergence de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Théorème de flux-divergence — En analyse vectorielle, le théorème de flux divergence, appelé aussi théorème de Green Ostrogradski, affirme l égalité entre l intégrale de la divergence d un champ vectoriel sur un volume dans et le flux de ce champ à travers la frontière du… …   Wikipédia en Français

  • Théorème de la divergence — Théorème de flux divergence Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème d'Ostrogradski — Théorème de flux divergence Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème d'Ostrogradsky — Théorème de flux divergence Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de Green-Ostrogradski — Théorème de flux divergence Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de Green-Ostrogradsky — Théorème de flux divergence Articles d analyse vectorielle …   Wikipédia en Français

  • Theoreme du gradient — Théorème du gradient Articles d analyse vectorielle Obj …   Wikipédia en Français

  • Theoreme de Helmholtz-Hodge — Théorème de Helmholtz Hodge Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de helmholtz-hodge — Articles d analyse vectorielle …   Wikipédia en Français

  • Théorème de Green-Riemann — Théorème de Green Articles d analyse vectorielle Objets …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”