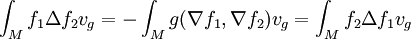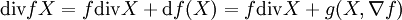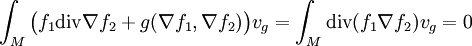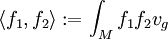- Opérateur de laplace-beltrami
-
Opérateur de Laplace-Beltrami
L'opérateur de Laplace-Beltrami est une généralisation de l'opérateur laplacien aux variétés riemanniennes. On part de la définition classique
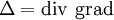 , et l'on est ramené à définir la divergence et le gradient dans le cadre riemannien.
, et l'on est ramené à définir la divergence et le gradient dans le cadre riemannien.Avertissement : Dans cet article, on utilise la convention de sommation d'Einstein. Même quand le signe somme n'est pas omis, on s'impose la discipline de ne sommer que par rapport à un indice qui se trouvant à la fois en positions inférieure et supérieure.
Sommaire
Divergence associée à une forme volume
Sur une variété différentielle M orientable, la divergence est naturellement associée à une forme volume. Si ω est une telle forme, toute autre forme de degré maximum s'écrit de façon unique fω, où f est une fonction. Cela s'applique à la dérivée de Lie de ω par rapport à un champ de vecteurs X. La divergence de X (par rapport à ω) est l'unique fonction telle que
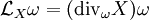 .
.D'après la formule
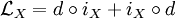 , on a
, on a 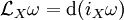 . Donc, d'après la formule de Stokes, si X est à support compact,
. Donc, d'après la formule de Stokes, si X est à support compact,Si ω s'écrit en cordonnées locales
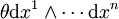 , on a
, on a(car
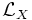 est une dérivation).
est une dérivation).Si
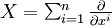 , on a
, on a 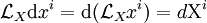 , d'où l'on tire
, d'où l'on tire 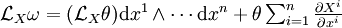 , et finalement,
, et finalement, 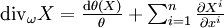 .
.Remarque sur l'orientabilité : L'introduction d'une forme volume suppose la variété orientable. Mais si on change la forme volume ω en son oppposée, divωX) ne change pas. En fait, la divergence ne dépend que de la densité associée à ω. Contrairement aux apparences, l'hypothèse d'orientabilté est inutile, on a en fait utilisé une orientation locale.
L'exemple le plus important est celui de la divergence définie par la forme volume canonique d'une métrique riemannienne.
En coordonnées locales
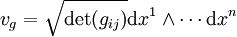 . D'après la remarque qui précède, il n'est nullement nécessaire de supposer la variété orientable. Le déterminant des gij est souvent noté g, notamment par ceux qui écrivent ds2 la métrique riemannienne, cela ne porte pas trop à confusion.
. D'après la remarque qui précède, il n'est nullement nécessaire de supposer la variété orientable. Le déterminant des gij est souvent noté g, notamment par ceux qui écrivent ds2 la métrique riemannienne, cela ne porte pas trop à confusion.Gradient associé à une métrique riemannienne
Le gradient d'une fonction (disons lisse) f est l'unique champ de vecteurs, noté
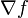 , tel que
, tel que 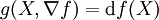 pour tout champ de vecteurs X. En coordonnées locales,
pour tout champ de vecteurs X. En coordonnées locales,Ici, gij(x) est l'inverse du tenseur métrique, défini en coordonnées par
où
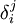 est le symbole de Kronecker.
est le symbole de Kronecker.Définition et propriétés de base du laplacien
On définit l'opérateur de Laplace-Beltrami comme l'opérateur différentiel du second ordre
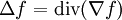 .
.En coordonnées locales,
Si f1 et f2 sont C2 et à support compact on a
Pour le voir, on remarque que si f est une fonction et X un champ de vecteurs,
En appliquant cette relation à f = f1 et
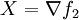 , on obtient
, on obtientpuisque d'après la formule de Stokes l'intégrale de la divergence d'un champ de vecteurs à support compact est nulle.
Cette formule exprime le fait que Δ est un opérateur formellement autoadjoint sur
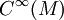 , par rapport au produit scalaire global, défini par
, par rapport au produit scalaire global, défini par(noter l'analogie avec les opérateurs symétriques en dimension finie.
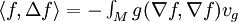 est négatif ou nul. L'opérateur − Δ est positif (c'est la raison pour laquelle beaucoup de géomètres riemanniens définissent l'opérateur de Laplace comme
est négatif ou nul. L'opérateur − Δ est positif (c'est la raison pour laquelle beaucoup de géomètres riemanniens définissent l'opérateur de Laplace comme 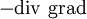 ). Enfin, si M est une variété compacte sans bord, les seules fonctions à Laplacien nul sont les constantes (de même que les seules fonctions harmoniques sur un domaine compact de
). Enfin, si M est une variété compacte sans bord, les seules fonctions à Laplacien nul sont les constantes (de même que les seules fonctions harmoniques sur un domaine compact de 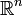 , nulles au bord sont les constantes, la preuve est d'ailleurs la même).
, nulles au bord sont les constantes, la preuve est d'ailleurs la même).Articles liés
- Variété différentielle
- Variété riemannienne
- Tenseur
- Théorie spectrale
- Formule sommatoire de Poisson
- Formule des traces de Selberg
- Formule des traces de Gutzwiller
Bibliographie
- Peter Sarnak ; Spectra of hyperbolic surfaces, Bulletin of the American Mathematical Society 40 (2003), 441-478. Texte disponible en ligne.
- Isaac Chavel, Eigenvalues in Riemannian geometry, Academic Press.
- Portail des mathématiques
- Portail de la physique
Catégories : Géométrie différentielle | Méthode mathématique de la physique | Géométrie riemannienne
Wikimedia Foundation. 2010.

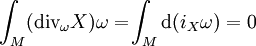
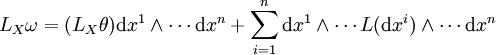
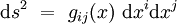
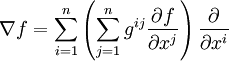
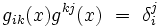
![\Delta \ = \ \frac{1}{\sqrt{g}} \ \partial_{i} \left[ \sqrt{g} g^{ij} \partial_{j} \right]](/pictures/frwiki/52/414fbc863e514cb776f01d8452bfc667.png)