Flux (Mathématiques)
- Flux (Mathématiques)
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Flux (Mathématiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Flux (mathématiques) — Pour les articles homonymes, voir Flux. En analyse vectorielle, on appelle flux d un champ vectoriel deux quantités scalaires analogues, selon qu on le calcule à travers une surface ou une courbe. Sommaire 1 Flux à travers une surface … Wikipédia en Français
Mathematiques financieres — Mathématiques financières Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant les marchés financiers. Elles utilisent… … Wikipédia en Français
Mathématiques Financières — Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant les marchés financiers. Elles utilisent principalement des outils issus de… … Wikipédia en Français
Mathematiques de la relativite generale — Mathématiques de la relativité générale Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils… … Wikipédia en Français
Mathématiques De La Relativité Générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la … Wikipédia en Français
MATHÉMATIQUES (DIDACTIQUE DES) — Les problèmes posés par l’enseignement des mathématiques ne sont pas nouveaux. Au début du siècle, Henri Lebesgue était préoccupé par les conditions de l’enseignement et de la formation des professeurs. Des efforts plus récents se sont déployés… … Encyclopédie Universelle
Mathématiques financières — Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant les marchés financiers. Elles utilisent principalement des outils issus de… … Wikipédia en Français
Mathématiques de la relativité générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la … Wikipédia en Français
Flux — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Flux », sur le Wiktionnaire (dictionnaire universel) Le mot flux (du latin fluxus, écoulement) désigne … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
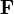 de
de 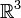 à travers la surface orientée Σ la quantité scalaire
à travers la surface orientée Σ la quantité scalaire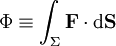
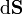 représente un vecteur normal élémentaire et
représente un vecteur normal élémentaire et  le produit scalaire. Si la surface est donnée par le paramétrage σ(u,v) (où u et v varient dans un ouvert Ω), ce vecteur est fourni par
le produit scalaire. Si la surface est donnée par le paramétrage σ(u,v) (où u et v varient dans un ouvert Ω), ce vecteur est fourni par![\mathrm d\mathbf S = \left[\frac{\partial\sigma}{\partial u}\times\frac{\partial\sigma}{\partial v} \right] \mathrm du\,\mathrm dv](/pictures/frwiki/53/570e8c8656b83cbdbe6d782f3e73748c.png)
![\Phi = \iint_\Omega \mathbf F\bigl(\sigma(u,v)\bigr) \cdot \left[\frac{\partial\sigma}{\partial u}\times\frac{\partial\sigma}{\partial v} \right] \mathrm du\,\mathrm dv = \iint_\Omega \det\left(\mathbf F,\tfrac{\partial\sigma}{\partial u},\tfrac{\partial\sigma}{\partial v} \right) \mathrm du\,\mathrm dv](/pictures/frwiki/102/f48c4902a7f5b073df98aca0736b6d67.png)
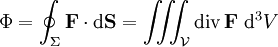
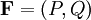 de
de 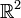 à travers la courbe Γ la quantité
à travers la courbe Γ la quantité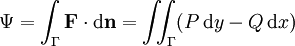
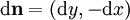 représente un vecteur normal élémentaire. Cela revient à définir le flux de
représente un vecteur normal élémentaire. Cela revient à définir le flux de 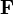 comme la circulation (ou intégrale curviligne) du champ orthogonal
comme la circulation (ou intégrale curviligne) du champ orthogonal 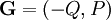 :
: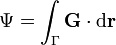
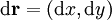 . Le flux d'un champ à travers une courbe, à l'inverse de sa circulation, ne dépend que de sa composante normale à la courbe.
. Le flux d'un champ à travers une courbe, à l'inverse de sa circulation, ne dépend que de sa composante normale à la courbe.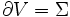 .
.