Theoreme de la base normale
- Theoreme de la base normale
-
Théorème de la base normale
En mathématique, le théorème de la base normale s'inscrit dans la théorie de Galois.
Il énonce que si 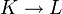 est une extension finie et galoisienne de corps commutatifs, de groupe de Galois G, alors il existe
est une extension finie et galoisienne de corps commutatifs, de groupe de Galois G, alors il existe 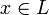 tel que l'orbite Gx soit une base du K-espace vectoriel L.
tel que l'orbite Gx soit une base du K-espace vectoriel L.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie de Galois | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de la base normale de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de la base normale — En mathématiques, le théorème de la base normale s inscrit dans la théorie de Galois. Il énonce que si est une extension finie galoisienne de corps commutatifs, de groupe de Galois G, alors il existe un élément x de L dont l orbite Gx est une… … Wikipédia en Français
Theoreme de Hilbert-Speiser — Théorème de Hilbert Speiser En mathématiques, le théorème de Hilbert Speiser est un résultat sur les corps cyclotomiques, caractérisant ceux avec une base intégrale normale. Plus généralement, il s applique à toute extension abélienne K du corps… … Wikipédia en Français
Théorème de hilbert-speiser — En mathématiques, le théorème de Hilbert Speiser est un résultat sur les corps cyclotomiques, caractérisant ceux avec une base intégrale normale. Plus généralement, il s applique à toute extension abélienne K du corps des nombres rationnels . Le… … Wikipédia en Français
Théorème de Hilbert-Speiser — En mathématiques, le théorème de Hilbert Speiser (de) est un résultat sur les sous corps des corps cyclotomiques, caractérisant ceux qui possèdent une base normale d entiers. D après le théorème de Kronecker Weber, les extensions abéliennes… … Wikipédia en Français
Base de Jordan — Réduction de Jordan Pour les articles homonymes, voir Jordan. La réduction de Jordan est la traduction matricielle de la réduction des endomorphismes introduite par Jordan. Cette réduction est tellement employée, en particulier en analyse pour la … Wikipédia en Français
Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… … Wikipédia en Français
Theoreme d'Abel (algebre) — Théorème d Abel (algèbre) Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 … Wikipédia en Français
Théorème d'Abel-Ruffini — Théorème d Abel (algèbre) Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 … Wikipédia en Français
Théorème d'Abel (Algèbre) — Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 … Wikipédia en Français
Théorème d'abel (algèbre) — Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 … Wikipédia en Français
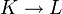 est une extension finie et galoisienne de corps commutatifs, de groupe de Galois G, alors il existe
est une extension finie et galoisienne de corps commutatifs, de groupe de Galois G, alors il existe 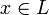 tel que l'orbite Gx soit une base du K-espace vectoriel L.
tel que l'orbite Gx soit une base du K-espace vectoriel L.