Représentation des groupes de Lie
- Représentation des groupes de Lie
-
Représentation d'un groupe de Lie
En géométrie différentielle, la représentation des groupes de Lie est une approche de l'étude des groupes de Lie par représentation comme groupe d'endomorphismes linéaires sur un espace vectoriel (voire comme groupe classique).
Pour un groupe de Lie réel donné G, une représentation réelle ou complexe de G est la donnée d'un espace vectoriel réel ou complexe V et d'un morphisme de groupes de Lie 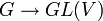 où GL(V) est le groupe des isomorphismes linéaires de V.
où GL(V) est le groupe des isomorphismes linéaires de V.
Nature des représentations
- Représentation irréductible
- Représentation totalement réductible
Classification des représentations
La classification des représentations d'un groupe de Lie G passe par l'étude des représentations de son algèbre de Lie g.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Groupe de Lie | Théorie des représentations des groupes de Lie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Représentation des groupes de Lie de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Représentation des groupes finis — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Representation des groupes — Représentation de groupe L idée générale de la théorie des représentations est d essayer d étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d où le… … Wikipédia en Français
Représentation des groupes — Représentation de groupe L idée générale de la théorie des représentations est d essayer d étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d où le… … Wikipédia en Français
Lexique Des Groupes De Lie — Liste incomplète, ajouter les définitions, améliorer, ajouter les termes manquants ... Algèbre de Borcherds Algèbre de Kac Moody Algèbre de Lie Algèbre de Lie nilpotente Algèbre de Lie semi simple Algèbre de Lie soluble Algèbre de Lie abélienne… … Wikipédia en Français
Lexique des groupes de lie — Liste incomplète, ajouter les définitions, améliorer, ajouter les termes manquants ... Algèbre de Borcherds Algèbre de Kac Moody Algèbre de Lie Algèbre de Lie nilpotente Algèbre de Lie semi simple Algèbre de Lie soluble Algèbre de Lie abélienne… … Wikipédia en Français
GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles … Encyclopédie Universelle
Representation d'algebre de Lie — Représentation d algèbre de Lie En mathématiques, une représentation d une algèbre de Lie est une façon d écrire cette algèbre comme une algèbre de matrices, ou plus généralement d endomorphismes d un espace vectoriel, avec le crochet de Lie… … Wikipédia en Français
Représentation d'algèbre de lie — En mathématiques, une représentation d une algèbre de Lie est une façon d écrire cette algèbre comme une algèbre de matrices, ou plus généralement d endomorphismes d un espace vectoriel, avec le crochet de Lie donné par le commutateur. Définition … Wikipédia en Français
Lexique des groupes de Lie — Liste incomplète, ajouter les définitions, améliorer, ajouter les termes manquants ... Algèbre de Borcherds Algèbre de Kac Moody Algèbre de Lie Algèbre de Lie nilpotente Algèbre de Lie semi simple Algèbre de Lie résoluble Algèbre de Lie abélienne … Wikipédia en Français
Représentation d'algèbre de Lie — En mathématiques, une représentation d une algèbre de Lie est une façon d écrire cette algèbre comme une algèbre de matrices, ou plus généralement d endomorphismes d un espace vectoriel, avec le crochet de Lie donné par le commutateur. Sommaire 1 … Wikipédia en Français
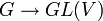 où GL(V) est le groupe des isomorphismes linéaires de V.
où GL(V) est le groupe des isomorphismes linéaires de V.