Représentation d'un groupe de lie
- Représentation d'un groupe de lie
-
Représentation d'un groupe de Lie
En géométrie différentielle, la représentation des groupes de Lie est une approche de l'étude des groupes de Lie par représentation comme groupe d'endomorphismes linéaires sur un espace vectoriel (voire comme groupe classique).
Pour un groupe de Lie réel donné G, une représentation réelle ou complexe de G est la donnée d'un espace vectoriel réel ou complexe V et d'un morphisme de groupes de Lie 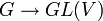 où GL(V) est le groupe des isomorphismes linéaires de V.
où GL(V) est le groupe des isomorphismes linéaires de V.
Nature des représentations
- Représentation irréductible
- Représentation totalement réductible
Classification des représentations
La classification des représentations d'un groupe de Lie G passe par l'étude des représentations de son algèbre de Lie g.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Groupe de Lie | Théorie des représentations des groupes de Lie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Représentation d'un groupe de lie de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Representation d'un groupe de Lie — Représentation d un groupe de Lie En géométrie différentielle, la représentation des groupes de Lie est une approche de l étude des groupes de Lie par représentation comme groupe d endomorphismes linéaires sur un espace vectoriel (voire comme… … Wikipédia en Français
Représentation d'un groupe de Lie — En géométrie différentielle, la représentation des groupes de Lie est une approche de l étude des groupes de Lie par représentation comme groupe d endomorphismes linéaires sur un espace vectoriel (voire comme groupe classique). Pour un groupe de… … Wikipédia en Français
Groupe De Lie Compact — Un groupe de Lie compact est un groupe de Lie réel ou complexe dont l espace topologique sous jecent est compact. Un groupe de Lie réel compact admet une métrique riemannienne invariante par translations à droite et à gauche. La classification… … Wikipédia en Français
Groupe de lie compact — Un groupe de Lie compact est un groupe de Lie réel ou complexe dont l espace topologique sous jecent est compact. Un groupe de Lie réel compact admet une métrique riemannienne invariante par translations à droite et à gauche. La classification… … Wikipédia en Français
Groupe de Lie compact — En mathématiques, un groupe de Lie compact est un groupe de Lie (réel ou complexe) qui, en tant que groupe topologique, est un groupe compact. Un groupe de Lie réel compact admet une métrique riemannienne invariante par translations à droite et à … Wikipédia en Français
Groupe De Lie — En mathématiques, un groupe de Lie est un groupe qui est continu, c est à dire que chaque élément du groupe peut être approché d aussi près que l on veut par une suite d autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu un… … Wikipédia en Français
Groupe de lie — En mathématiques, un groupe de Lie est un groupe qui est continu, c est à dire que chaque élément du groupe peut être approché d aussi près que l on veut par une suite d autres éléments du groupe. Un groupe de Lie est en fait un peu plus qu un… … Wikipédia en Français
Groupe de Lie E8 — E8 (mathématiques) Pour les articles homonymes, voir E8. Le polytope de Gosset : les 240 vecteurs du système de racines En mathématiques … Wikipédia en Français
Groupe de Lie — En mathématiques, un groupe de Lie est un groupe « lisse », c est à dire qu il possède une structure différentiable pour laquelle les opérations de groupe – multiplication et inversion – sont différentiables. Les groupes de Lie sont… … Wikipédia en Français
Représentation d'un groupe topologique — En mathématiques, une représentation continue, ou représentation d un groupe topologique est une représentation de ce groupe sur un espace vectoriel topologique qui est continue en tant qu action. Sommaire 1 Définition 2 Autres notions de… … Wikipédia en Français
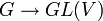 où GL(V) est le groupe des isomorphismes linéaires de V.
où GL(V) est le groupe des isomorphismes linéaires de V.