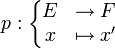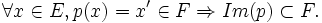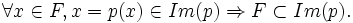Opérateur de projection

En algèbre linéaire, le projecteur est un endomorphisme qu'on peut présenter de deux façons équivalentes

• c'est une projection linéaire associée à une décomposition de E comme somme de deux sous-espaces supplémentaires, c'est-à-dire qu'elle permet d'obtenir un des termes de la décomposition correspondante
• c'est aussi un endomorphisme idempotent : il vérifie p²=p

On peut aussi définir, dans un espace de Hilbert, le projecteur sur un convexe fermé (notion topologique et non plus algébrique)

• c'est l'application qui a tout élément de l'espace associe l'élément du convexe le plus proche
• dans le cas où le convexe est un sous-espace vectoriel, on retrouve un cas particulier de projection orthogonale

Sommaire 1 Définition de la projection vectorielle 1.1 Propriétés 1.2 Identification des projecteurs et des projections 1.3 Projecteur associé à un autre projecteur 2 Projecteurs associés à une famille d'espaces supplémentaires 3 Symétries 4 Projecteurs orthogonaux 5 Représentation matricielle en base adaptée 6 Voir aussi 6.1 Articles connexes

Définition de la projection vectorielle

Soit F un sous-espace vectoriel de E, G un supplémentaire dans E. N'importe quel vecteur x de E peut s'écrire d'une façon unique comme somme d'un vecteur de F et d'un vecteur de G : 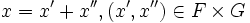. La projection p sur F parallèlement à G est alors l'application p qui associe à tout x de E le vecteur x' de F.

Propriétés

• Im(p)=F :
  • 
  • 
• Ker(p)=G :
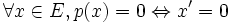  • et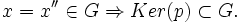
  • 
• 

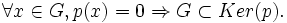
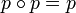
Identification des projecteurs et des projections

Définissons les projecteurs de E comme les endomorphismes p de E vérifiant p²=p. On vient de voir que toute projection est un projecteur. On prouve maintenant la réciproque.

Théorème de caractérisation des projecteurs

Tout projecteur de E est une projection, précisément la projection sur Im p parallèlement à Ker p. Notamment si p est un projecteur Im p et Ker p sont des sous-espaces supplémentaires.

• Démonstration : on fait une démonstration valable en toute dimension

• les deux espaces sont en somme directe : si x est dans leur intersection, x est de la forme p(y) et vérifie p(x)=0=p²(y)=p(y)=x.
• tout vecteur x de E se décompose, sous la forme (d'ailleurs unique) x = p(x) + [x − p(x)]

Le premier élément est dans Im p, le second dans Ker p.

Finalement « projecteurs » et « couples d'espaces vectoriels supplémentaires » se correspondent bijectivement.

Projecteur associé à un autre projecteur

La projection sur G parallèlement à F est l'application q=Id-p, appelé aussi projecteur associé à p.

L'image de q n'est autre que le noyau de p, l'image de p est le noyau de q.

Projecteurs associés à une famille d'espaces supplémentaires

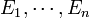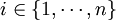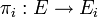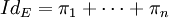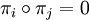Un espace vectoriel E est somme directe de sous espaces vectoriels si et seulement si pour tout il existe des projecteurs vérifiant : et si .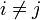

Symétries

Une symétrie vectorielle est un endomorphisme s tel que s² est l'identité (ne pas confondre avec endomorphisme symétrique).

• p est un projecteur si et seulement si s=2p-Id est une symétrie vectorielle

La recherche des endomorphismes tels que p²=p, ou que s²=Id effectuée ici est un cas particulier simple du traitement de l'équation P(u)=0 pour P polynôme et u endomorphisme, voir l'article polynôme d'endomorphisme pour des généralisations.

Projecteurs orthogonaux

• Dans un espace quadratique, un projecteur est un endomorphisme symétrique si et seulement si 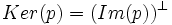. On a alors un projecteur orthogonal, ou une projection orthogonale.

Représentation matricielle en base adaptée

En choisissant une base de l'espace qui soit la réunion d'une base du noyau et d'une base de l'image (ce qui est possible, car image et noyau sont supplémentaires), on obtient une représentation matricielle vérifiant les propriétés suivantes :

• Sur la diagonale apparaissent uniquement des "1" et des "0", et le nombre de "1" est égal au rang du projecteur ;
• Les autres coefficients sont nuls.

Voir aussi

Articles connexes

• Projection (géométrie)

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau