Idempotent

Idempotent

Idempotence

En mathematiques et en informatique, le concept d' idempotence signifie basiquement qu'une opération a le même effet qu'on l'applique une ou plusieurs fois, ou encore qu'en la réappliquant on ne modifiera pas le résultat. On la retrouve en algèbre générale, en particulier dans la théorie des opérateurs de projections et des opérateurs de clôture.

Sommaire

Définition

En mathématiques, un élément x d'un anneau A est dit idempotent si x2 = x,

Plus généralement x\, est dit idempotent d'ordre n s'il vérifie l'égalité suivante: xn = x.

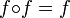En particulier, une application f est idempotente si f{\circ}f=f.

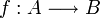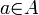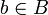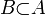Autrement dit, si f:A\longrightarrow B est idempotente alors si f(a) = b (avec a{\in}A, b\in{B} et B{\subset}A) alors f(f(a)) = b.

Nombres idempotents

En considérant, dans ce paragraphe, l'opération multiplication on a :

Dans 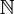\mathbb N , 0 et 1 sont idempotents sur tous les ordres

Dans 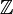\mathbb Z , on peut rajouter -1 qui est idempotent pour les ordres impairs

Dans \mathbb C , i et -i sont idempotents d'ordre 5

Endomorphismes idempotents

Un endomorphisme linéaire idempotent est appelé "projecteur".

Si E est un espace vectoriel et u un endomorphisme idempotent d'ordre 2, u est appelé projecteur. On l'interprète géométriquement comme la projection de l'espace image de u sur le noyau de u.

Si E est un espace vectoriel complexe de dimension finie et u un endomorphisme idempotent, alors u est diagonalisable, avec des valeurs propres qui sont toutes racines n-èmes de l'unité.

En Informatique

En informatique, le terme est utilisé pour décrire des fonctions, procédures, méthodes ou routines qui peuvent être appelées plusieurs fois sans problèmes car le système maintient le même état après une ou plusieurs invocations: toutes les variables gardent la valeur qu'elles avaient après la première invocation.

Par exemple: Rechercher le nom d'un client dans une base de données est typiquement idempotent, car cela ne change pas la base de données. Placer une commande n'est pas idempotent, car plusieurs invocations résulteront en plusieurs commandes. Annuler une commande au contraire est idempotent car la commande reste annulée quel que soit le nombre d'invocations.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Idempotence ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Idempotent de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • idempotent — ● idempotent, idempotente adjectif Élément idempotent d un ensemble muni d une loi interne ⊤, élément de l ensemble qui vérifie x ⊤ x = x. ● idempotent, idempotente (expressions) adjectif Élément idempotent d un ensemble muni d une loi interne ⊤ …   Encyclopédie Universelle

  • idempotent — 1870, from L. idem the same + potentem powerful (see POTENT (Cf. potent)) …   Etymology dictionary

  • Idempotent — Idempotenz ist ein Begriff aus der Mathematik und Informatik. Er bezeichnet die Eigenschaft einer Funktion, in Verknüpfung mit sich selbst das gleiche Ergebnis zu liefern wie bei einmaliger Verwendung. Die beiden grundlegenden und wichtigsten… …   Deutsch Wikipedia

  • idempotent — adjective Etymology: Latin idem same + potent , potens having power more at potent Date: 1870 relating to or being a mathematical quantity which when applied to itself under a given binary operation (as multiplication) equals itself; also… …   New Collegiate Dictionary

  • idempotent — /uy deuhm poht nt, id euhm /, Math. adj. 1. unchanged when multiplied by itself. n. 2. an idempotent element. [1865 70; IDEM + POTENT1] * * * …   Universalium

  • idempotent — i•dem•po•tent [[t]ˈaɪ dəmˈpoʊt nt, ˈɪd əm [/t]] Math. 1) math. (of a number or matrix) unchanged when multiplied by itself 2) math. an idempotent element • Etymology: 1870; idem+potent I …   From formal English to slang

  • idempotent — adjective unchanged in value following multiplication by itself this matrix is idempotent • Similar to: ↑unchanged • Topics: ↑mathematics, ↑math, ↑maths …   Useful english dictionary

  • Idempotent measure — In mathematics, an idempotent measure on a metric group is a probability measure that equals its convolution with itself; in other words, an idempotent measure is an idempotent element in the topological semigroup of probability measures on the… …   Wikipedia

  • idempotent — adjective Describing an action which, when performed multiple times, has no further effect on its subject after the first time it is performed. In algebra, x nbsp;= nbsp;x for all positive n. See Also: idempotence, nilpotent, nullipotent,… …   Wiktionary

  • idempotent — idempotẹnt,   Mathematik: bezeichnet ein Element a eines Rings, für das a2 = a gilt …   Universal-Lexikon

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”