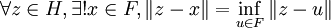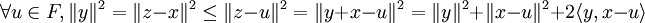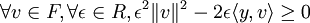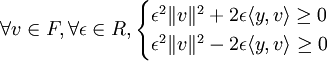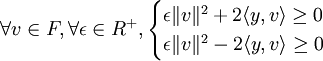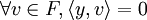Théorème du supplémentaire orthogonal d'un fermé dans un Hilbert

Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert

Le théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert est un théorème d'analyse fonctionnelle.

Énoncé

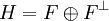
Si $H$ est un espace de Hilbert, et $F$ un sous-espace vectoriel fermé de $H$ , alors l'orthogonal de $F$ est un sous-espace supplémentaire de $F$ , c'est-à-dire que $H = F \oplus F^\bot$

Démonstration

$F$ est un espace vectoriel, donc convexe, et fermé par hypothèse. On peut donc appliquer le théorème de projection sur un convexe fermé :

$\forall z \in H, \exists! x \in F, \|z-x\|=\inf_{u\in F} \|z-u\|$

Notons $y = z - x$ . Par définition de $x$ , on a:

$\forall u \in F, \|y\|^2 = \|z-x\|^2 \le \|z-u\|^2 = \|y+x-u\|^2 =\|y\|^2+\|x-u\|^2+2\langle y,x-u\rangle$

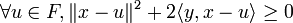d'où $\forall u \in F, \|x-u\|^2 + 2\langle y,x-u\rangle \ge 0$ .

Prenons $v$ et posons $u = x + ε v$ . L'inéquation devient alors

$\forall v \in F, \forall \epsilon \in R, \epsilon^2 \|v\|^2-2\epsilon \langle y,v\rangle \ge 0$

D'où, en choisissant d'abord un $ε$ puis son opposé dans l'expression ci-dessus :

$\forall v \in F, \forall \epsilon \in R,\begin{cases}\epsilon ^2\|v\|^2+2\epsilon\langle y,v\rangle \ge 0 \\ \epsilon ^2\|v\|^2-2\epsilon\langle y,v\rangle \ge 0\end{cases}$

d'où, en se restreignant à $R +$ et en simplifiant par $ε$ :

$\forall v \in F, \forall \epsilon \in R^+,\begin{cases}\epsilon \|v\|^2+2\langle y,v\rangle \ge 0 \\ \epsilon \|v\|^2-2\langle y,v\rangle \ge 0\end{cases}$

d'où, en faisant tendre $ε$ vers 0,

$\forall v \in F, \langle y,v\rangle =0$

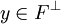c'est-à-dire $y \in F^\bot$ .

Et donc on peut décomposer $z$ en

$z=x+ y, x \in F, y \in F^\bot$

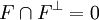Comme on a toujours $F \cap F^\bot = 0$ ,

on peut donc enfin conclure

$H = F \oplus F^\bot$

Conséquences

L'application $p F$ qui a $z$ associait $x$ , ci-dessus, définie en minimisant une distance, s'appelle le projecteur sur $F$ .

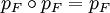Il a bien la particularité d'un projecteur au sens classique (bien que défini topologiquement, et non algébriquement), i.e. $p_F\circ p_F=p_F$ .

Lorsque, comme dans notre cas, 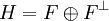$H = F \oplus F^\bot$ on appelle ce projecteur le projecteur orthogonal sur $F$ , et on peut préciser de noyau 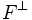$F^\bot$ et d'image $F$ .

On peut alors montrer que $p F$ est linéaire.

En effet, par unicité de la décomposition dans deux sous-espaces vectoriels orthogonaux et supplémentaires, si 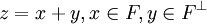$z=x+ y, x \in F, y \in F^\bot$ , alors $p F (z) = x$ .

Du coup, soient $z = x + y, z' = x' + y'$ les décompositions de deux vecteurs, on en déduit la décomposition $z + λ z' = (x + λ x') + (y + λ y')$ et donc $p F (z + λ z') = x + λ x' = p F (z) + λ p F (z')$ .

On retombe bien sur la définition algébrique habituelle d'un projecteur, que l'on connaissait bien pour les espaces de dimension finie.

Théorèmes de l'analyse fonctionnelle

Théorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram

modifier

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me du suppl%C3%A9mentaire orthogonal d%27un ferm%C3%A9 dans un espace de Hilbert ».

Catégories : Théorème de mathématiques | Espace de Hilbert

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème du supplémentaire orthogonal d'un fermé dans un Hilbert de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme du supplementaire orthogonal d'un ferme dans un espace de Hilbert — Théorème du supplémentaire orthogonal d un fermé dans un espace de Hilbert Le théorème du supplémentaire orthogonal d un fermé dans un espace de Hilbert est un théorème d analyse fonctionnelle. Énoncé Si H est un espace de Hilbert, et F un sous… … Wikipédia en Français
Théorème du supplémentaire orthogonal d'un fermé dans un espace de hilbert — Le théorème du supplémentaire orthogonal d un fermé dans un espace de Hilbert est un théorème d analyse fonctionnelle. Énoncé Si H est un espace de Hilbert, et F un sous espace vectoriel fermé de H, alors l orthogonal de F est un sous espace… … Wikipédia en Français
Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert — Le théorème du supplémentaire orthogonal d un fermé dans un espace de Hilbert est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstrations 2.1 Par le théorème de projection sur un convexe … Wikipédia en Français
Théorème de projection sur un convexe fermé — En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance dont le principal corollaire est l existence d un supplémentaire orthogonal, donc d une projection orthogonale sur un sous… … Wikipédia en Français
Theoreme de representation de Riesz — Théorème de représentation de Riesz Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces … Wikipédia en Français
Théorème de Fréchet-Riesz — Théorème de représentation de Riesz Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces … Wikipédia en Français
Théorème de représentation de riesz — Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces de Hilbert 1.1 Énoncé 1.2 … Wikipédia en Français
Théorème de représentation de Riesz — Pour les articles homonymes, voir Théorème de Riesz. Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz … Wikipédia en Français
Theoreme de Lax-Milgram — Théorème de Lax Milgram Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi… … Wikipédia en Français
Théorème de lax-milgram — Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi notamment de fondement à la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème du supplémentaire orthogonal d'un fermé dans un Hilbert

Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert

Énoncé

Démonstration

Conséquences

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème du supplémentaire orthogonal d'un fermé dans un Hilbert

Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert

Énoncé

Démonstration

Conséquences

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link