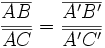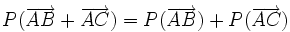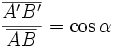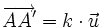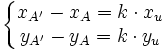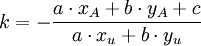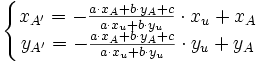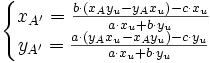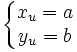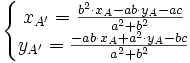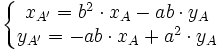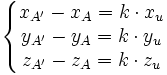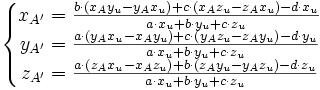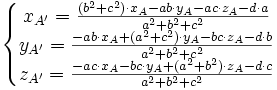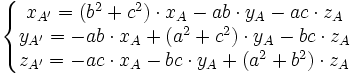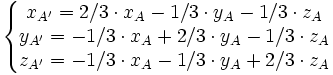Projection (géométrie)

Pour les articles homonymes, voir Projection.

En géométrie, une projection est une transformation de l'espace, c'est-à-dire une application linéaire qui projette l'espace sur une sous partie. Par exemple pour faire de la 3D on projette l'espace (en 3D) sur l'écran (en 2D), on obtient ainsi un rendu similaire à celui que l'on aurait eu en regardant la même scène avec ses propres yeux.

Projection en géométrie plane

En géométrie plane, on considère une droite D du plan et une direction Δ non parallèle à D. Soit un point A du plan, alors la projection de A sur D selon Δ est le point A' = P(A) tel que :

Si A est sur D, alors A = A' ;
sinon :
- A' est situé sur D ;
- la droite (AA' ) est parallèle à Δ.

En géométrie euclidienne, on fait fréquemment usage d'un cas particulier de projection linéaire, la projection orthogonale : c'est le cas particulier où Δ est perpendiculaire à D. Dans ce cas-là, si A est hors de D, alors (AA') est perpendiculaire à D.

La projection est une application linéaire. Cela signifie que si A, B et C sont trois points alignés et si A', B' et C' sont leurs projetés, alors

$\frac{\overline{AB}}{\overline{AC}} = \frac{\overline{A'B'}}{\overline{A'C'}}$

(on oriente les droites) ou encore

$P(\overrightarrow{AB} + \overrightarrow{AC}) = P(\overrightarrow{AB}) + P(\overrightarrow{AC})$

et si k est un scalaire, alors

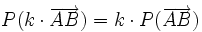$P(k \cdot \overrightarrow{AB}) = k\cdot P(\overrightarrow{AB})$ .

Projections et coordonnées cartésiennes

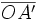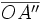Les droites D et Δ se coupent en O. Alors, soient A' le projeté de A sur D parallèlement à Δ, et A'' le projeté de A sur Δ parralèllement à D. On voit que $\overline{OA'}$ et $\overline{OA''}$ définissent des coordonnées cartésiennes de A dans le repère (O, D, Δ), les droites D et Δ étant orientées et normées.

Projection et trigonométrie

Considérons une projection orthogonale sur D. Soient deux point A et B, et soit α l'angle 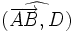$(\widehat{\overrightarrow{AB},D})$ . Alors

$\frac{\overline{A'B'}}{\overline{AB}} = \cos \alpha$

Projection parallèlement à une droite en géométrie analytique

Soit $\vec{u}$ un vecteur directeur de Δ de composantes (x_u, y_u). Soit

a·x + b·y + c = 0

l'équation de D. Soit le point A de coordonnées (x_A, y_A) et son projeté A' de coordonnées (x_A', y_A').

Comme (AA' ) est parallèle à Δ, il existe un scalaire k tel que

$\overrightarrow{AA'} = k \cdot \vec{u}$

soit

$\left \{ \begin{matrix} x_{A'} - x_A = k \cdot x_u \\ y_{A'} - y_A = k \cdot y_u \end{matrix} \right.$

Par ailleurs, A' est sur D, ce qui signifie que

a·x_A' + b·y_A' + c = 0

on obtient donc

a·(k·x_u + x_A) + b·(k·y_u + y_A) + c = 0

d'où

$k = -\frac{a \cdot x_A + b\cdot y_A +c}{a \cdot x_u + b \cdot y_u}$

(a·x_u + b·y_u est non nul puisque $\vec{u}$ n'est pas colinéaire à D) d'où

$\left \{ \begin{matrix} x_{A'} = -\frac{a \cdot x_A + b\cdot y_A + c}{a \cdot x_u + b \cdot y_u} \cdot x_u + x_A\\ y_{A'} = -\frac{a \cdot x_A + b\cdot y_A + c}{a \cdot x_u + b \cdot y_u} \cdot y_u + y_A \end{matrix} \right.$

soit

$\left \{ \begin{matrix} x_{A'} = \frac{b \cdot (x_A y_u - y_A x_u) - c \cdot x_u}{a \cdot x_u + b \cdot y_u}\\ y_{A'} = \frac{a \cdot (y_A x_u - x_A y_u) - c \cdot y_u}{a \cdot x_u + b \cdot y_u} \end{matrix} \right.$

Dans le cas d'une projection orthogonale, et si le repère est orthonormé, alors on peut choisir

$\left \{ \begin{matrix} x_u = a \\ y_u = b \end{matrix} \right.$

ce qui donne

$\left \{ \begin{matrix} x_{A'} = \frac{b^2 \cdot x_A - ab \cdot y_A - ac}{a^2 + b^2}\\ y_{A'} = \frac{- ab \cdot x_A + a^2 \cdot y_A - bc}{a^2 + b^2} \end{matrix} \right.$

on peut alors vérifier que si l'on prend la projection orthogonale sur l'axe Ox (qui a pour équation y = 0 soit a = c = 0 et b = 1), on a bien x_A' = x_A et y_A' = 0.

Si l'on décide arbitrairement que D contient l'origine (c = 0) et que a² + b² = 1, on obtient alors

$\left \{ \begin{matrix} x_{A'} = b^2 \cdot x_A - ab \cdot y_A \\ y_{A'} = - ab \cdot x_A + a^2 \cdot y_A \end{matrix} \right.$

Projection en géométrie dans l'espace

Projection sur un plan parallèlement à une droite

Exemple de projection orthogonale sur un plan

Considérons un plan Π et une droite Δ. Soit A un point de l'espace. La projection P sur Π parallèlement à Δ est définie par :

P(A) est sur Π ;
si A est sur Π, alors P(A) = A ;
sinon, la droite (A, P(A)) est parallèle à Δ.

Si Δ est perpendiculaire à Π, alors la projection est dite orthogonale.

La projection est une application linéaire, on retrouve donc des propriétés de la projection en géométrie plane : si A, B et C sont trois points alignés et si A', B' et C' sont leurs projetés, alors

$\frac{\overline{AB}}{\overline{AC}} = \frac{\overline{A'B'}}{\overline{A'C'}}$

(on oriente les droites) ou encore

$P(\overrightarrow{AB} + \overrightarrow{AC}) = P(\overrightarrow{AB}) + P(\overrightarrow{AC})$

et si k est un scalaire, alors

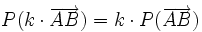$P(k \cdot \overrightarrow{AB}) = k\cdot P(\overrightarrow{AB})$ .

Projection sur un plan parallèlement à une droite en géométrie analytique

Soit $\vec{u}$ un vecteur directeur de Δ de composantes (x_u, y_u, z_u). Soit

a·x + b·y + c·z + d = 0

l'équation de Π. Soit le point A de coordonnées (x_A, y_A, z_A) et son projetté A' de coordonnées (x_A', y_A', z_A').

Comme (AA' ) est parallèle à Δ, il existe un scalaire k tel que

$\overrightarrow{AA'} = k \cdot \vec{u}$

soit

$\left \{ \begin{matrix} x_{A'} - x_A = k \cdot x_u \\ y_{A'} - y_A = k \cdot y_u \\ z_{A'} - z_A = k \cdot z_u \\ \end{matrix} \right.$

Par ailleurs, A' est sur Π, ce qui signifie que

a·x_A' + b·y_A' + c·z_A' + d = 0

On voit que d'un point de vue analytique, le problème est très similaire au précédent. On a un système de quatre équations à quatre inconnues x_A', y_A', z_A' et k. On obtient :

$\left \{ \begin{matrix} x_{A'} = \frac{b \cdot (x_A y_u - y_A x_u) + c \cdot (x_A z_u - z_A x_u) - d \cdot x_u}{a \cdot x_u + b \cdot y_u + c \cdot z_u} \\ y_{A'} = \frac{a \cdot (y_A x_u - x_A y_u) + c \cdot (y_A z_u - z_A y_u) - d \cdot y_u}{a \cdot x_u + b \cdot y_u + c \cdot z_u} \\ z_{A'} = \frac{a \cdot (z_A x_u - x_A z_u) + b \cdot (z_A y_u - y_A z_u) - d \cdot z_u}{a \cdot x_u + b \cdot y_u + c \cdot z_u} \\ \end{matrix} \right.$

Dans le cas d'une projection orthogonale et si le repère est orthonormal, on peut choisir x_u = a, y_u = b et z_u = c, soit

$\left \{ \begin{matrix} x_{A'} = \frac{(b^2 + c^2) \cdot x_A - ab \cdot y_A - ac \cdot z_A - d \cdot a}{a^2 + b^2 + c^2} \\ y_{A'} = \frac{-ab \cdot x_A + (a^2 + c^2) \cdot y_A - bc \cdot z_A - d \cdot b}{a^2 + b^2 + c^2} \\ z_{A'} = \frac{-ac \cdot x_A - bc \cdot y_A + (a^2 + b^2) \cdot z_A - d \cdot c}{a^2 + b^2 + c^2} \\ \end{matrix} \right.$

Si l'on décide arbitrairement que Π contient l'origine (d = 0) et que a² + b² + c² = 1, alors on a

$\left \{ \begin{matrix} x_{A'} = (b^2 + c^2) \cdot x_A - ab \cdot y_A - ac \cdot z_A \\ y_{A'} = -ab \cdot x_A + (a^2 + c^2) \cdot y_A - bc \cdot z_A \\ z_{A'} = -ac \cdot x_A - bc \cdot y_A + (a^2 + b^2) \cdot z_A \\ \end{matrix} \right.$

Dans le cas de la perspective isométrique, on choisit |a| = |b| = |c| = 1/√3. Par exemple, si on choisit les trois valeurs positives, on a

$\left \{ \begin{matrix} x_{A'} = 2/3 \cdot x_A - 1/3 \cdot y_A - 1/3 \cdot z_A \\ y_{A'} = -1/3 \cdot x_A + 2/3 \cdot y_A - 1/3 \cdot z_A \\ z_{A'} = -1/3 \cdot x_A - 1/3 \cdot y_A + 2/3 \cdot z_A \\ \end{matrix} \right.$

Projection sur une droite parallèlement à un plan

Avec les mêmes notations que ci-dessus, on peut définir la projection Q sur Δ parallèlement à Π :

Q(A) est sur Δ ;
si A est sur Δ, alors Q(A) = A ;
sinon, la droite (A, Q(A)) est coplanaire à Π.

Si Δ est perpendiculaire à Π, alors la projection est dite orthogonale.

C'est toujours une applicaiton linéaire, elle a donc les propriétés énoncées ci-dessus.

Projections et coordonnées cartésiennes

Considérons trois droites D₁, D₂ et D₃, non coplanaires et concourante en un point O. Elles sont normées et orientées.

Pour un point de l'espace A, on appelle :

A₁ le projetté de A sur D₁ parallèlement au plan (D₂, D₃) ;
A₂ le projetté de A sur D₂ parallèlement au plan (D₃, D₁) ;
A₃ le projetté de A sur D₃ parallèlement au plan (D₁, D₂).

Alors, (O,D₁, D₂, D₃) forme un repère et 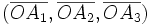$(\overline{OA_1}, \overline{OA_2}, \overline{OA_3})$ sont les coordonnées de A dans ce repère.

Projection centrale

En géométrie projective, on considère des projections centrales. Elles décrivent ce qui arrive aux positions observées de différents objets quand l'œil de l'observateur change de place. Les transformations projectives en sont la généralisation.

Définition générale

En algèbre linéaire une projection est une application naturellement associée à une décomposition de l'espace sous forme de deux sous-espaces supplémentaires. À un vecteur de l'espace, elle associe l'un des deux éléments de sa décomposition sur ces deux espaces.

Voir l'article détaillé Projecteur (mathématiques).

À ce titre, la projection centrale n'est pas un projecteur.

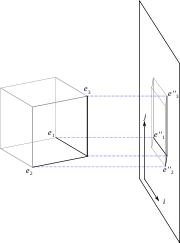
En synthèse d'image 3D

Article détaillé : Rastérisation.

Une projection 3D est une transformation mathématique utilisée en synthèse d'image 3D pour faire une perspective (projeter des points en trois dimensions sur un plan en deux dimensions). Elle est souvent utilisée pour simuler la relation entre une caméra et son sujet. La projection 3D est souvent la première étape dans le processus de dessin d'objets 3D sur un écran informatique, processus connu sous le nom de rendu. Les algorithmes suivants étaient très employés dans les premières simulations sur ordinateur et les jeux vidéo, et le sont toujours avec quelques grosses modifications pour chaque cas particulier. Cet article ne décrit que le cas le plus simple, le plus général.

Données nécessaires à la projection 3D

Les données utilisées pour dessiner les objets sont en général stockées sous la forme de collections de points, liés ensemble en triangles. Chaque point est une série de trois nombres, représentant les coordonnées X, Y, et Z du point, relativement a l'origine de l'objet. Chaque triangle est une série de trois points, ou trois index de points. En plus de cela, l'objet a trois coordonnées X,Y,Z, et trois valeurs représentant ses angles de rotation. Cela permet de gérer sa position et sa rotation, toutes deux relatives à un « monde ». Pour finir, l'observateur (le terme caméra est celui communément admis) : la caméra a elle aussi trois coordonnées X,Y,Z pour sa position, et trois angles pour sa rotation. Toutes ces données sont en général stockées sous forme de nombres flottants, même si beaucoup de programmes les convertissent en nombres entiers, pour accélérer les calculs.

Projection orthogonale en synthèse d'image

Voir Perspective axonométrique > Projection orthogonale en synthèse d'image.

Projection centrale en synthèse d'image 3D

Une formule simplifiée permet de calculer les coordonnées à l'écran d'un point.

2D.X = 3D.X - ((DX / (3D.Z + Distance)) * 3D.X)

2D.Y = 3D.Y - ((DY / (3D.Z + Distance)) * 3D.Y)

où 2D.X et 2D.Y sont les coordonnées finales projetées sur l'écran, 3D.X, 3D.Y, et 3D.Z les coordonnées du point à projeter, Distance une constante, et DX et DY la distance respectivement en X et Y entre la caméra et le point. On écrit encore plus simplement :

2D.X = 3D.X / (3D.Z * fov)

2D.Y = 3D.Y / (3D.Z * fov)

Cette formule est mathématiquement incorrecte mais donne de bons résultats à moindre coût. Si fov vaut 1, nous aurons une projection isométrique, sans notion de profondeur.

Voir aussi

Regardez d'autres dictionnaires:

Projection orthogonale — En mathématiques, la projection orthogonale est une transformation de l espace, une application linéaire : en géométrie plane, c est une projection telle que les deux droites la droite sur laquelle on projette et la direction de projection… … Wikipédia en Français
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Projection centrale — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques … Wikipédia en Français
Projection stéréographique — du pôle sud sur le plan équatorial … Wikipédia en Français
Geometrie descriptive — Géométrie descriptive La géométrie descriptive est avant tout une méthode pour résoudre de façon graphique sur le papier des problèmes d intersections et d ombres entre volumes et surfaces définis de façon géométrique dans l espace à trois… … Wikipédia en Français
Géométrie Descriptive — La géométrie descriptive est avant tout une méthode pour résoudre de façon graphique sur le papier des problèmes d intersections et d ombres entre volumes et surfaces définis de façon géométrique dans l espace à trois dimensions. Ces problèmes… … Wikipédia en Français
Geometrie projective — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques … Wikipédia en Français
Géométrie Projective — La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques 2 Aperçu élémentaire … Wikipédia en Français
projection — [ prɔʒɛksjɔ̃ ] n. f. • 1314; lat. projectio, de projectus, p. p. de projicere 1 ♦ Action de jeter, de lancer en avant (⇒ 1. jet; projeter, I ). Projection de liquide, de vapeur. Lancement, jet (de projectiles). Projection de pierres, d obus.… … Encyclopédie Universelle
GÉOMÉTRIE ALGÉBRIQUE — Sous sa forme actuelle, la géométrie algébrique est une branche de l’algèbre relativement récente (cf. ALGÈBRE, DEDEKIND). Pour «comprendre» les phénomènes d’intersection des courbes et des surfaces, il s’est révélé nécessaire d’élaborer des… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Projection (géométrie)