- Algorithme du simplexe
-
L'algorithme du simplexe de George Dantzig est une technique à la fois fondamentale et très populaire pour les problèmes d'optimisation linéaire. Ainsi, étant donné un ensemble d'inégalités linéaires sur n variables réelles, l'algorithme permet de minimiser (ou maximiser) une fonction objectif, qui est elle aussi linéaire (l'algorithme fonctionne encore quand la fonction est croissante en chacune des n variables).
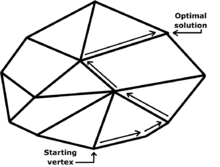
En termes géométriques, l'ensemble des inégalités linéaires définit un polytope dans l'espace à n dimensions (polygone en 2 dimensions et polyèdre en 3 dimensions) et il s'agit de trouver le sommet optimal pour la fonction de coût donnée. En effet, la fonction que l'on cherche à minimiser étant linéaire sur le polytope, elle y est en particulier concave. Or une fonction concave et minorée sur un polytope admet un minimum en un des sommets du polytope. La recherche d'un point de minimum peut donc se restreindre aux sommets du polytope (qui peuvent être très nombreux néanmoins).
L'idée de l'algorithme consiste à partir d'un sommet quelconque du polytope et, à chaque itération, d'aller à un sommet adjacent s'il est possible d'en trouver un meilleur pour la fonction objectif. S'il n'y en a pas, l'algorithme s'arrête en concluant que le sommet courant est optimal. En général, il y a plusieurs sommets adjacents au sommet courant qui sont meilleurs pour l'objectif. Il faut en sélectionner un seul, la règle de sélection est appelée règle de pivotage.
Il a été montré pour les principales règles de pivotage employées que l'algorithme du simplexe pouvait prendre un temps de calcul exponentiel. En particulier, on ne sait pas s'il existe une règle de pivotage qui assurerait que l'algorithme se termine après un nombre polynomial d'étapes.
On peut montrer que le nombre d'itérations de l'algorithme est majoré par :
où ν est le plus petit nombre d'arêtes reliées à un même sommet du polytope parcouru par le simplexe et N est le nombre de sommets. On remarquera que ν est minoré par la dimension de l'espace dans lequel vit le polytope.Néanmoins, l'algorithme du simplexe est très efficace en pratique et il est implémenté dans tous les solveurs de programmes linéaires. Les autres algorithmes de résolution de programmes linéaires sont basés soit sur la méthode de l'ellipsoïde soit sur la méthode du point intérieur.
Voir aussi
Liens externes
- (en) Simplex Algorithm. Illustration détaillée de l'exécution de l'algorithme (version « tableau »).
- (fr) [PDF] Exemple de l'algorithme du Simplexe. L’algorithme du simplexe appliqué de manière très didactique à un exemple (version « tableau »).
Catégories :- Algorithme numérique
- Algorithme d'optimisation
- Algorithmique et convexité
Wikimedia Foundation. 2010.
