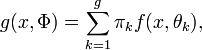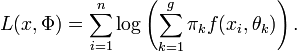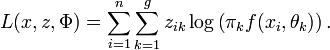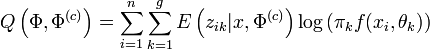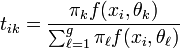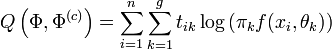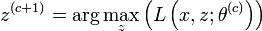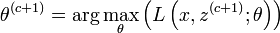- Algorithme esperance-maximisation
-
Algorithme espérance-maximisation
L'algorithme espérance-maximisation (en anglais Expectation-maximisation algorithm, souvent abrégé EM), proposé par Dempster et al. (1977), est une classe d'algorithmes qui permettent de trouver le maximum de vraisemblance des paramètres de modèles probabilistes lorsque le modèle dépend de variables latentes non observables.
On utilise souvent Espérance-maximisation pour la classification de données, en apprentissage machine, ou en vision artificielle. Espérance-maximisation alterne des étapes d'évaluation de l'espérance (E), où l'on calcule l'espérance de la vraisemblance en tenant compte des dernières variables observées, et une étape de maximisation (M), où l'on estime le maximum de vraisemblance des paramètres en maximisant la vraisemblance trouvée à l'étape E. On utilise ensuite les paramètres trouvés en M comme point de départ d'une nouvelle phase d'évaluation de l'espérance, et l'on itère ainsi.
Pour résoudre le problème d'apprentissage des modèles de Markov cachés (HMM), c’est-à-dire la détermination des paramètres du modèle markovien, on utilise l'algorithme de Baum-Welch.
Sommaire
Principe de fonctionnement
En considérant un échantillon
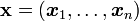 d'individus suivant une loi
d'individus suivant une loi 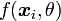 paramétrée par
paramétrée par 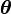 , on cherche à déterminer le paramètre
, on cherche à déterminer le paramètre 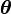 maximisant la log-vraisemblance donnée par
maximisant la log-vraisemblance donnée par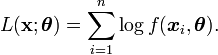
Cet algorithme est particulièrement utile lorsque la maximisation de L est très complexe mais que, sous réserve de connaître certaines données judicieusement choisies, on peut très simplement déterminer
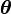 .
.Dans ce cas, on s'appuie sur des données complétées par un vecteur
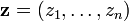 inconnnu. En notant
inconnnu. En notant 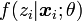 la probabilité de zi sachant
la probabilité de zi sachant 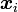 et le paramètre
et le paramètre 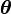 , on peut définir la log-vraisemblance complétée comme la quantité
, on peut définir la log-vraisemblance complétée comme la quantité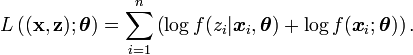
et donc,
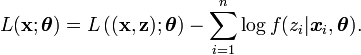
L'algorithme EM est une procédure itérative basée sur l'espérance des données complétées conditionnellement au paramètre courant. En notant
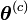 ce paramètre, on peut écrire
ce paramètre, on peut écrire![E\left[L(\mathbf{x};\boldsymbol{\theta})|\boldsymbol{\theta}^{(c)}\right]=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]-E\left[\sum_{i=1}^n\log f(z_i|\boldsymbol{x}_i,\boldsymbol{\theta}))|\boldsymbol{\theta}^{(c)}\right],](/pictures/frwiki/57/9535ef81a8157f8d9e4b8af81bea0d1c.png)
ou encore
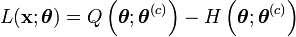
avec
![Q\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]](/pictures/frwiki/51/38f8b92ae34438b9c8fb9552037b6fdb.png) et
et ![H\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[\sum_{i=1}^n\log f(z_i|\boldsymbol{x}_i,\boldsymbol{\theta}))|\boldsymbol{\theta}^{(c)}\right]](/pictures/frwiki/51/3fe5f7864f12cd9db840f88ea740db47.png) .
.On montre que la suite définie par
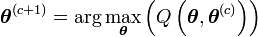
fait tendre
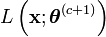 vers un maximum local.
vers un maximum local.On peut donc définir l'algorithme EM de la manière suivante:
- Initialisation au hasard de
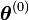
- c=0
- Tant que l'algorithme n'a pas convergé, faire
-
- Evaluation de l'espérance (étape E) :
![Q\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]](/pictures/frwiki/51/38f8b92ae34438b9c8fb9552037b6fdb.png)
- Maximisation (étape M) :
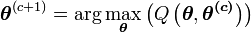
- c=c+1
- Evaluation de l'espérance (étape E) :
- Fin
En pratique, pour s'affranchir du caractère local du maximum atteint, on fait tourner l'algorithme EM un grand nombre de fois à partir de valeurs initiales différentes de manière à avoir de plus grandes chances d'atteindre le maximum global de vraisemblance.
Exemple détaillé: application en classification automatique
Une des applications phares d'EM est l'estimation des paramètres d'une densité mélange en classification automatique dans le cadre des modèles de mélanges gaussiens. Dans ce problème, on considère qu'un échantillon
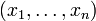 de
de 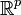 , ie caractérisé par p variables continues, est en réalité issu de g différents groupes. En considérant que chacun de ces groupes Gk suit une loi f de paramètre θk, et dont les proportions sont données par un vecteur
, ie caractérisé par p variables continues, est en réalité issu de g différents groupes. En considérant que chacun de ces groupes Gk suit une loi f de paramètre θk, et dont les proportions sont données par un vecteur 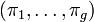 . En notant
. En notant 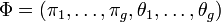 le paramètre du mélange, la fonction de densité que suit l'échantillon est donnée par
le paramètre du mélange, la fonction de densité que suit l'échantillon est donnée paret donc, la log-vraisemblance du paramètre Φ est donnée par
La maximisation de cette fonction selon Φ est très complexe. Par exemple, si on souhaite déterminer les paramètres correspondant à 2 groupes suivant une loi normale dans un espace de dimension 3 (ce qui est peu), on doit optimiser une fonction non linéaire de
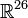 !!!
!!!Parallèlement, si on connaissait les groupes auxquels appartient chacun des individus, alors le problème serait un problème d'estimation tout à fait simple et très classique.
La force de l'algorithme EM est justement de s'appuyer sur ces données pour réaliser l'estimation. En notant zik la grandeur qui vaut 1 si l'individu xi appartient au groupe Gk et 0 sinon, la log-vraisemblance des données complétée s'écrit
On obtient alors rapidement
En notant tik la quantité donnée par
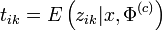 , on peut séparer l'algorithme EM en deux étapes, qu'on appelle classiquement, dans le cas des modèles de mélanges, l'étape Estimation et l'étape Maximisation. Ces deux étapes sont itérées jusqu'à la convergence.
, on peut séparer l'algorithme EM en deux étapes, qu'on appelle classiquement, dans le cas des modèles de mélanges, l'étape Estimation et l'étape Maximisation. Ces deux étapes sont itérées jusqu'à la convergence.- Etape E: calcul de tik par la règle d'inversion de Bayes:
- Etape M: Détermination de Φ maximisant
L'avantage de cette méthode est qu'on peut séparer le problème en g problèmes élémentaires qui sont, en général relativement simple. Dans tous les cas, les proportions optimales sont données par
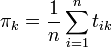
L'estimation des θ dépend par ailleurs de la fonction de probabilité f choisie. Dans le cas normal, il s'agit des moyennes μk et des matrices de variance-covariance Σk. Les estimateurs optimaux sont alors donnée par
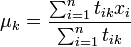
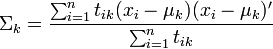
Avec M' la matrice transposée de M et en supposant que les μk sont des vecteurs colonnes.
Variantes usuelles d'EM
L'algorithme EM, bien que très performant et souvent simple à mettre en œuvre, pose quand même parfois quelques problèmes qui ont donné lieu à des développements complémentaires. Parmi ceux-ci, nous évoquerons un développement appelé GEM (Generalized EM) qui permet de simplifier le problème de l'étape maximisation, un autre, appelé CEM (Classification EM) permettant de prendre en compte l'aspect classification lors de l'estimation, et un dernier, SEM (Stochastic EM) dont l'objectif est de réduire le risque de tomber dans un optimum local de vaisemblance.
Algorithme GEM
GEM a été proposé en même temps qu'EM par Dempster et al. (1977) qui ont prouvé que pour assurer la convergence vers un maximum local de vraisemblance, il n'est pas nécessaire de maximiser Q à chaque étape mais qu'une simple amélioration de Q est suffisante.
GEM peut donc s'écrire de la manière suivante:
- Initialisation au hasard de
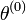
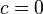
- Tant que l'algorithme n'a pas convergé, faire
-
- choisir
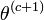 tel que
tel que 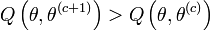
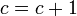
- choisir
- Fin
Algorithme CEM
L'algorithme EM se positionne dans une optique estimation, c'est-à-dire qu'on cherche à maximiser la vraisemblance du paramètre
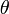 , sans considération de la classification faite a posteriori en utilisant la règle de Bayes.
, sans considération de la classification faite a posteriori en utilisant la règle de Bayes.L'approche classification, proposée par Celeux et Govaert (1991) consiste à optimiser, non pas la vraisemblance du paramètre, mais directement la vraisemblance complétée, donnée, dans le cas des modèles de mélange, par
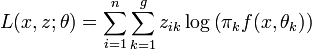
Pour cela, il suffit de procéder de la manière suivante:
- Initialisation au hasard de
- Tant que l'algorithme n'a pas convergé, faire
- Fin
Algorithme SEM
Afin de réduire le risque de tomber dans un maximum local de vraisemblance, Celeux et Diebolt (1985) proposent d’intercaler une étape stochastique de classification entre les étapes E et M. Après le calcul des probabilités
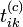 , l’appartenance
, l’appartenance 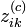 des individus aux classes est tirée aléatoirement selon une loi multinomiale de paramètres
des individus aux classes est tirée aléatoirement selon une loi multinomiale de paramètres 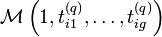 .
.Contrairement à ce qui se produit dans l’algorithme CEM, on ne peut considérer que l’algorithme a convergé lorsque les individus ne changent plus de classes. En effet, celles-ci étant tirées aléatoirement, la suite
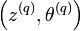 ne converge pas au sens strict. En pratique, Celeux et Diebolt (1985) proposent de lancer l’algorithme SEM un nombre de fois donné puis d’utiliser l’algorithme CEM pour obtenir une partition et une estimation du paramètre
ne converge pas au sens strict. En pratique, Celeux et Diebolt (1985) proposent de lancer l’algorithme SEM un nombre de fois donné puis d’utiliser l’algorithme CEM pour obtenir une partition et une estimation du paramètre 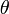 .
.Voir aussi
Références
- Celeux, G. et Diebolt, D. (1985). The sem algorithm : a probabilistic teacher algorithm derived from the em algorithm for the mixture problem. Computational Statistics Quarterly, 2(1) :73–82.
- Celeux, G. et Govaert, G. (1991). A classification EM algorithm for clustering and two stochastic versions. Rapport de recherche RR-1364, Inria, Institut National de Recherche en Informatique et en Automatique.
- Dempster, A. P., Laird, N. M. et Rubin, D. B. (1977). Maximum likelihood from incomplete data via the em algorithm (with discussion). Journal of the Royal Statistical Society, B 39 :1–38.
- Portail des probabilités et des statistiques
- Portail de l’informatique
Catégories : Optimisation | Statistiques | Algorithmique | Apprentissage automatique - Initialisation au hasard de
Wikimedia Foundation. 2010.