- Colinéaires
-
Colinéarité
En géométrie vectorielle, deux vecteurs
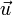 et
et 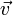 sont colinéaires s'il existe un scalaire k tel que
sont colinéaires s'il existe un scalaire k tel que 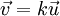 ou
ou 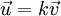 .
.Étymologiquement, on remarque que colinéaire signifie sur une même ligne. En effet, en géométrie affine, deux vecteurs sont colinéaires si et seulement s'il existe deux représentants de ces vecteurs situés sur une même droite i.e. il existe trois points A, B, C alignés tels que
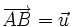 et
et 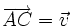
La colinéarité est une notion importante en géométrie affine car elle permet de définir
- l'alignement : les points A, B et C sont alignés si et seulement si les vecteurs
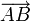 et
et 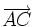 sont colinéaires.
sont colinéaires. - le parallélisme de deux droites : les droites (AB) et (CD) sont parallèles si et seulement si les vecteurs
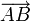 et
et 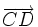 sont colinéaires
sont colinéaires
On peut remarquer que le vecteur nul est colinéaire à tout autre vecteur de l'espace vectoriel.
Sur l'ensemble des vecteurs non nuls, la relation de colinéarité est
- réflexive : un vecteur est colinéaire à lui-même
- symétrique : Si un vecteur
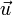 est colinéaire à un vecteur
est colinéaire à un vecteur 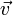 alors
alors 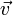 est colinéaire à
est colinéaire à 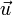
- transitive :Si un vecteur
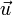 est colinéaire à
est colinéaire à 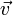 et si
et si 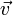 est colinéaire à
est colinéaire à 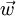 alors
alors 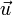 est colinéaire à
est colinéaire à 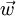
Ce qui permet de dire que (sur l'ensemble des vecteurs non nuls) la relation de colinéarité est une relation d'équivalence dont les classes d'équivalence forment l'espace projectif associé à l'espace vectoriel
Montrer la colinéarité de deux vecteurs grâce à leurs coordonnées
Soit
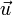 et
et 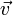 deux vecteurs quelconques du plan tel que
deux vecteurs quelconques du plan tel que 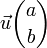 et
et 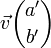 alors:
alors: 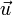 et
et 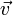 sont colinéaires si et seulement si : a'b − ab' = 0
sont colinéaires si et seulement si : a'b − ab' = 0Voir aussi
Catégories : Géométrie affine | Espace vectoriel
Wikimedia Foundation. 2010.


