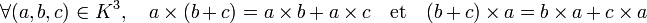- Catégorie des corps
-
Corps (mathématiques)
 Pour les articles homonymes, voir Corps.
Pour les articles homonymes, voir Corps.En mathématiques, et plus précisément en algèbre, un corps est une structure algébrique. De manière informelle, un corps est un ensemble dans lequel il est possible d'effectuer des additions, des soustractions, des multiplications et des divisions.
Des exemples élémentaires de corps sont le corps des nombres rationnels (noté
 ), le corps des nombres réels (noté
), le corps des nombres réels (noté  ), le corps des nombres complexes (noté
), le corps des nombres complexes (noté  ) et le corps
) et le corps 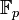 des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.
des congruences modulo p où p est un nombre premier. L'exemple le plus simple de corps non commutatif (parfois appelés anneau à division, suivant l'anglais) est celui des quaternions.La théorie des corps est appelée, par certains, théorie de Galois[réf. nécessaire] ; cependant, la théorie de Galois désigne en général une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, qui forment l'exemple historique, mais s'étend aussi à bien d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. Autrement dit, la théorie de Galois est une branche de la théorie des corps.
Sommaire
Fragments d'histoire
Jusqu'au XIXe siècle, les ensembles de nombres ont paru tellement naturels que l'on ne s'est jamais préoccupé de leur donner un nom, ni même de définir avec précision leur structure [1]. Cependant, avec la naissance de l'étude des nombres algébriques, il est apparu d'autres ensembles de nombres que les rationnels, les réels et les complexes. Il est devenu nécessaire de préciser la structure de corps, puis la notion d'entiers sur ce corps et enfin la notion d'anneau. C'est à l'école allemande que l'on doit le développement de ces notions. C'est Richard Dedekind qui définit pour la première fois la structure de corps (Körper en allemand) [2] et c'est la raison pour laquelle un corps quelconque est souvent nommé K ou
 . La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.
. La structure de corps s'insère dans une hiérarchie comprenant le monoïde, le groupe, l'anneau, et donne lieu à la définition de l'espace vectoriel, et de l'algèbre.Définition et exemple
Un corps est un ensemble K muni de deux lois internes notées en général + et × vérifiant
- (K, +) forme un groupe commutatif dont l'élément neutre est noté 0
- (K \ {0}, ×) forme un groupe multiplicatif.
- la multiplication est distributive pour l'addition (à gauche comme à droite) c’est-à-dire que
On parle alors du corps (K, +, ×)
Les premiers corps étudiés étant des ensembles de nombres (rationnels, réels, complexes, algébriques), la multiplication y était commutative. C'est la raison pour laquelle, initialement, dans la définition d'un corps, la multiplication devait être commutative. Actuellement, la tendance est plutôt de ne pas exiger la commutativité de la multiplication[3] ou du moins de préciser la nature des corps étudiés [4]; on appelle alors corps commutatif un corps dont la multiplication est commutative. Les corps non commutatifs sont parfois appelés corps gauches ou anneaux à division. Cette terminologie est inspirée de l'anglais où un corps commutatif est appelé field et un corps non nécessairement commutatif division ring.
Exemples de corps
- L'ensemble des nombres rationnels,
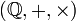 est un corps commutatif
est un corps commutatif - L'ensemble des nombres réels
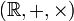 est un corps commutatif
est un corps commutatif - L'ensemble des complexes
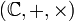 est un corps commutatif
est un corps commutatif - L'ensemble des quaternions
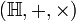 est un corps non commutatif
est un corps non commutatif - En arithmétique modulaire, l'ensemble
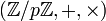 , où p est un nombre premier, est un corps commutatif.
, où p est un nombre premier, est un corps commutatif.
Un sous-corps d'un corps K est une partie non vide L de K, stable par + et
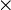 , telle que L munie des lois induites soit un corps.
, telle que L munie des lois induites soit un corps.Caractéristique
Article détaillé : Caractéristique d'un anneau.S'il existe un entier naturel n non nul tel que
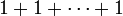 (avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut).
(avec n termes) est nul, on appelle caractéristique du corps le plus petit entier positif non nul vérifiant cette propriété. S'il n'existe pas d'entier non nul vérifiant cette propriété, on dit que le corps est de caractéristique nulle (parfois aussi grande que l'on veut).Par exemple le corps
 est de caractéristique nulle alors que le corps
est de caractéristique nulle alors que le corps 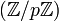 est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.
est de caractéristique p. On démontre qu'un corps possède toujours pour caractéristique soit 0 soit un nombre premier.Corps finis
Article détaillé : Corps fini.Ce sont les corps dont le nombre d'éléments est fini. L'étude des corps finis est tardive dans l'étude des corps. On démontre qu'un corps fini est toujours commutatif, de cardinal égal à la puissance d'un nombre premier. Il est en fait possible de dresser la liste de tous les corps finis (à isomorphisme près).
Le plus petit corps fini est celui des booléens, dont voici les tables d'addition et de multiplication:
addition + 0 1 0 0 1 1 1 0 multiplication x 0 1 0 0 0 1 0 1 Les corps finis les plus connus sont les corps de congruences modulo un nombre premier comme dans le cas ci-dessus, mais il en existe une infinité d’autres, comme par exemple ceux-ci, respectivement à quatre et neuf éléments, dont nous donnons ci-dessous les « tables de Pythagore », successivement pour la première loi de composition dite « addition », puis pour la deuxième dite « multiplication ». Nous désignons dans chaque cas comme a l’élément neutre de la première loi de composition, b celui de la deuxième.
Quatre éléments :
addition + a b c d a a b c d b b a d c c c d a b d d c b a multiplication x a b c d a a a a a b a b c d c a c d b d a d b c
Neuf éléments :addition + a b c d e f g h i a a b c d e f g h i b b c a e f d h i g c c a b f d e i g h d d e f g h i a b c e e f d h i g b c a f f d e i g h c a b g g h i a b c d e f h h i g b c a e f d i i g h c a b f d e multiplication x a b c d e f g h i a a a a a a a a a a b a b c d e f g h i c a c b g i h d f e d a d g c f i b e h e a e i f g b h c d f a f h i b d e g c g a g d b h e c i f h a h f e c g i d b i a i e h d c f b g Corps et anneau
L'ensemble
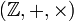 n'est pas un corps car la plupart des éléments de
n'est pas un corps car la plupart des éléments de 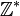 ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.
ne sont pas inversibles : par exemple, il n'existe pas d'entier relatif n tel que 2n = 1 donc 2 n'est pas inversible.Plus généralement, un ensemble A muni de deux lois + et × vérifiant
- (A, +) forme un groupe commutatif dont l'élement neutre est noté 0
- (A-{0}, ×) forme un monoïde.
- la multiplication est distributive pour l'addition (à gauche comme à droite)
est un anneau unitaire.
Article détaillé : Anneau (mathématiques).Si l'anneau A est intègre, c’est-à-dire si
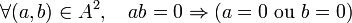 ,
,
ou encore,
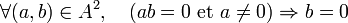
l'anneau est presque un corps car il ne lui manque plus que l'inversibilité pour la multiplication.
- On démontre que si l'anneau A est commutatif intègre, on peut le plonger dans son corps des fractions, qui est le plus petit corps contenant l'anneau.
Article détaillé : Corps des fractions.Exemple :
 est le corps des fractions de
est le corps des fractions de 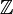
Un anneau intègre (unitaire) est un corps si et seulement si {0} et A (les idéaux triviaux) sont les seuls idéaux.
Un anneau intègre (unitaire) A est un corps si et seulement si tout A-module est libre.
Corps et espace vectoriel
Article détaillé : Espace vectoriel.Partant du corps
 , il est naturel de s'intéresser à
, il est naturel de s'intéresser à  , ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur
, ensemble des n-uplet de réels. On est amené à le munir d'une addition et d'une multiplication par un réel. La structure ainsi définie (une addition interne munissant l'ensemble d'une structure de groupe et une multiplication externe possédant des propriétés de distributivité et d'associativité) est appelée espace vectoriel sur  . Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.
. Il est alors naturel de définir ce que pourrait être un espace vectoriel sur un corps K quelconque.Corps et équation algébrique
L'étude des polynômes à coefficient dans un corps commutatif et la recherche de leurs racines a développé considérablement la notion de corps. Si f est un polynôme de degré n sur un corps commutatif K, l'équation f(x) = 0 est une équation algébrique dans K. Si, de plus, f est un polynôme irréductible, l'équation est dite irréductible. Lorsque n ≥ 2, trouver les solutions d'une telle équation demande de se placer dans un corps plus grand que K, une extension de corps.
Par exemple, l'équation x2 − 2 = 0 est irréductible dans
 mais possède des racines dans
mais possède des racines dans  ou mieux dans
ou mieux dans ![\mathbb Q[\sqrt 2]](/pictures/frwiki/100/db51c502f6ea3908be57943d0ba5af9a.png) . L'équation x2 + 1 = 0 ne possède pas de solution dans
. L'équation x2 + 1 = 0 ne possède pas de solution dans  mais en possède dans
mais en possède dans  ou mieux dans
ou mieux dans ![\mathbb Q[i]](/pictures/frwiki/50/2830a273d48073b03c768cce92401ea7.png) .
.Un corps de rupture d'un polynôme est, par exemple, un corps minimal contenant K et une racine de f.
Le corps de décomposition de f est le plus petit corps contenant K ainsi que toutes les racines de f.
L'étude des corps de décomposition d'un polynôme et du groupe de permutations de ses racines forme la branche des mathématiques que l'on appelle la théorie de Galois.
Propriétés
- Soit
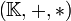 un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans
un corps commutatif. Alors tout polynôme de degré n admet au plus n zéros (ou racines) dans  .
.
- Soit
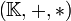 un corps commutatif. Alors tout sous-groupe fini de
un corps commutatif. Alors tout sous-groupe fini de 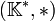 est un groupe cyclique.
est un groupe cyclique.
Preuve-
- Le nombre de racines d'un polynôme est inférieur ou égal à son degré.
L'anneau K[X] possède une division euclidienne, il est donc euclidien et par voie de conséquence factoriel (cf l'article anneau euclidien). Il est donc décomposable en produit de polynômes irréductibles. Si un polynôme irréductible P[X] n'est pas de degré 1, alors il n'admet pas de racine. En effet, si k est un élément du corps, la division euclidienne montre que le polynôme X - k divise tout polynôme ayant k pour racine. Le polynôme P[X], n'ayant pas de diviseur de degré 1, ne peut avoir de racine.
En conséquence, un polynôme quelconque admet autant de racines que sa décomposition en facteurs irréductibles contient de polynôme de degré 1, car un corps est intègre. Le fait qu'un produit de polynômes admet comme degré la somme des degrés des polynômes du produit permet de conclure.
-
- Tout sous-groupe fini du groupe multiplicatif est cyclique :
Soit G un tel sous-groupe, n son cardinal et e son exposant. L'exposant d'un groupe est le plus petit commun multiple des ordres des éléments du groupe. Le polynôme Xe - 1 admet chaque élément du groupe comme racine. Comme dans un corps commutatif, un polynôme n'admet jamais plus de racines que son degré, e est au moins égal à n. Le théorème de Lagrange montre que e est au plus égal à n et e est égal à n. Il existe toujours un élément g d'ordre l'exposant dans un groupe abélien fini (cf l'article exposant d'un groupe), en conséquence, g est d'ordre n et donc générateur du groupe G ce qui montre son caractère cyclique.
Autres champs d'étude
On retrouve la théorie des corps dans l'étude de certaines fonctions comme les fonctions rationnelles ou les fonctions elliptiques
Structures additionnelles
Voir aussi
Notes et références
- ↑ Bourbaki, (Élément d'histoire des mathématiques p 71-74) place l'émergence du concept de loi de composition et de structure au XIXe siècle chez Gauss puis l'école Allemande
- ↑ R.Dedekind, Gesammelte mathematische Werke, d'après Éléments d'histoire des mathématiques, Nicolas Bourbaki (p 106, ref 79)
- ↑ À la suite de Nicolas Bourbaki (Algèbre, chapitre 1), Lelong-Ferrand et Arnaudiès (Algèbre) et de nombreux auteurs définissent le corps comme pouvant ne pas être commutatif
- ↑ Deschamps-Warusfel (J'intègre) ou Lang (Algebra) précisent : « Dans la suite, on appellera corps un corps commutatif »
Liens internes
Sources
- Jacques Bouveresse, Jean Itard, Émile Sallé, Histoire des mathématiques [détail des éditions]
- Lelong-Ferrand, Arnaudies , Algèbre
- Petite encyclopédie des mathématiques, Editions K Pagoulatos
- Portail des mathématiques
Catégorie : Théorie des corps
Wikimedia Foundation. 2010.