Extension Normale

Extension normale

En mathématiques, une extension normale L de K est un cas particulier d'extension de corps. Une extension est dite normale si et seulement si tout morphisme de corps laissant invariant K est un automorphisme de L.

Cette propriété est utilisée pour définir une extension de Galois. Par définition, dans le cas d'une extension séparable alors toute extension finie normale est une extension de Galois.

Motivation

Le théorème fondamental de la théorie de Galois montre qu'il existe une correspondance féconde entre une extension finie L sur K et son groupe de Galois, si le groupe est suffisamment riche. Le groupe de Galois désigne l'ensemble des automorphismes de corps de L laissant K invariant.

Soit P[X] un polynôme à coefficients dans K avec une racine r dans L. Chaque morphisme de corps de L a pour image de r une autre racine de P[X]. Pour que le groupe de Galois soit suffisamment riche, il est nécessaire que toutes ces racines soient dans L. Ce qui se traduit par le fait que tout morphisme a pour image L.

Une autres condition est nécessaire, elle est liée à la séparabilité et est traitée dans l'article Extension séparable. Si les deux conditions sont réunies, alors l'extension est dite de Galois et les conditions du théorème fondamental sont réunies.

Dans le cas ou la séparabilité est garantie, par exemple parce que le corps K est parfait, alors il est possible de trouver une bonne extension normale. Par exemple, dans le cas d'un polynôme à coefficients dans un corps K parfait, il existe une plus petite extension normale contenant les racines du polynôme, c'est le corps de décomposition du polynôme.

Le théorème fondatemental de la théorie de Galois possède de nombreuses applications. Citons par exemple le théorème d'Abel qui donne une condition nécessaire et suffisante pour qu'une équation polynômiale soit résoluble par radicaux.

Le concept de normalité est développé dans l'article extension de Galois.

Définition

Soit K un corps, L une extension de corps de K. L'extension L est dite normale si et seulement si une des propositions équivalentes est respectée :

(1) Tout morphisme de corps de L laissant invariant K et à valeur dans Ω, la clôture algébrique de K, est un automorphisme de L.

(2) Tout polynôme irréductible à coefficients dans K ayant au moins une racine dans L a toutes ses racines dans L (ie. que tout polynôme irréductible de K[X] ayant une racine dans L se décompose en facteurs linéaire dans L[x]).

Propriétés

Les propriétés des extensions normales sont développées et démontrées dans l'article Extension de Galois. Rappelons ici une propriété importante. Ici L désigne une extension finie de K.

Le cardinal du groupe de Galois est inférieur ou égal à la dimension de L sur K.

C’est-à-dire que l'ensemble des automorphismes de L laissant K invariant et dont l'image de L est égal à L est toujours de cardinal inférieur ou égal à la dimension de L.

Exemple

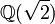$\mathbb{Q}(\sqrt{2})$ est une extension normale de $\mathbb{Q}$ car il est le corps de décomposition de $x 2 - 2$ . Mais $\mathbb{Q}(\sqrt[3]{2})$ n'est pas une extension normale de $\mathbb{Q}$ étant donné que $\mathbb{Q}(\sqrt[3]{2})$ contient la racine $\sqrt[3]{2}$ du polynôme $x 3 - 2$ mais pas les 2 autres racines (non réelles).

Articles de mathématiques en rapport avec la théorie de Galois
Corps	Corps fini · Corps parfait · Corps de rupture · Corps de décomposition
Extension de corps	Extension algébrique · Extension quadratique · Extension simple · Extension normale · Extension séparable · Extension de Galois · Groupe de Galois · Clôture algébrique
Articles associés	Caractéristique · Polynôme formel · Polynôme cyclotomique · Théorie de Galois · Théorème fondamental de la théorie de Galois · Théorème de l'élément primitif · Théorie d'Iwasawa

Portail des mathématiques

Ce document provient de « Extension normale ».

Catégorie : Théorie de Galois

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Extension Normale de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Extension normale — En mathématiques, une extension normale L de K est un cas particulier d extension de corps. Une extension algébrique est dite normale ou quasi galoisienne si et seulement si tout morphisme de corps de L dans un corps le contenant et induisant l… … Wikipédia en Français
Extension De Galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français
Extension de galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français
Extension galoisienne — Extension de Galois En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de … Wikipédia en Français
Extension Quadratique — En mathématiques, et plus précisément en algèbre dans le cadre de la théorie de Galois, une extension quadratique est une extension de corps de dimension deux. Si K est un corps commutatif, souvent celui des nombres rationnels, alors une… … Wikipédia en Français
Extension De Corps — En mathématiques, plus particulièrement en algèbre, l extension d un corps K est un corps L qui contient K comme sous corps. Par exemple, , le corps des nombres complexes, est une extension de , le corps des nombres réels, lequel est lui même un… … Wikipédia en Français
Extension Algébrique — En mathématiques et plus particulièrement en algèbre, une extension algébrique L sur un corps K est une extension de corps dans laquelle tous les éléments sont algébriques sur K c’est à dire sont racines d un polynôme non nul à coefficients dans… … Wikipédia en Français
Extension algebrique — Extension algébrique En mathématiques et plus particulièrement en algèbre, une extension algébrique L sur un corps K est une extension de corps dans laquelle tous les éléments sont algébriques sur K c’est à dire sont racines d un polynôme non nul … Wikipédia en Français
Extension Simple — En mathématiques et plus précisément en algèbre dans le cas de la théorie de Galois, une extension de corps L d un corps K est dite simple si et seulement s il existe un élément l de L tel que L est égal à K[l]. Une extension simple est finie si… … Wikipédia en Français
Extension Séparable — Une extension algébrique L d un corps K est dite séparable si et seulement si le polynôme minimal de tout élément de L n admet que des racines simples. Ce critère est une hypothèse nécessaire pour établir un théorème important de la théorie de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Extension Normale