Catégorie des schémas

Catégorie des schémas

Schéma (géométrie algébrique)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Schéma.

En géométrie algébrique, un schéma est un espace localement annelé localement isomorphe à un schéma affine.

Un schéma affine est le spectre d'un anneau commutatif unitaire, muni de son faisceau structural.

Intuition

Un schéma est avant tout un objet géométrique.

Telle qu'elle a été inventée, cette notion généralise la notion de variété algébrique. À une variété algébrique sur un corps, la théorie des schémas ajoute des points qui ne sont pas nécessairement fermés (grosso modo, ce sont des points dont les coordonnées sont des variables).

En théorie des nombres, pour étudier les propriétés arithmétiques d'une variété algébrique V sur ℚ, il est utile de connaître son comportement "modulo p" pour tout nombre premier p. Pour ce faire, on essaie d'étendre V d'une manière raisonnable en un schéma sur l'anneau des entiers relatifs \mathbb{Z}. 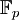Ce schéma peut être vu comme une famille de variétés algébriques {V, Vp} où Vp est une variété algébrique sur le corps fini premier \mathbb F_p.

Histoire

La notion de schéma est due à Alexander Grothendieck, qui l'a inventée dans le but de démontrer les conjectures de Weil (qui sont maintenant un théorème, démontré par Pierre Deligne) vers l'année 1958. La théorie des schémas est développée de la façon la plus belle et la plus complète dans le grand traité de fondements, inachevé (mais très complet !), les Éléments de géométrie algébrique, plus connu des mathématiciens sous le nom des EGA.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Sch%C3%A9ma (g%C3%A9om%C3%A9trie alg%C3%A9brique) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Catégorie des schémas de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Catégorie des variétés différentielles — Variété (géométrie) Pour les articles homonymes, voir Variété. Réalisation du ruban de Möbius, à partir du collage d une bande de papier. Le bord n est que d …   Wikipédia en Français

  • Schémas de classification — Schéma de classification Dans les métadonnées un schéma de classification correspond à l information descriptive d une organisation ou division d objets en groupes, basés sur des caractèristiques communes des objets. Le standard de registre de… …   Wikipédia en Français

  • Schémas de Liaison à la Terre — Schéma de liaison à la terre Pour les articles homonymes, voir SLT. En électricité, un Schéma de Liaison à la Terre, ou SLT (Anciennement Régime de neutre) définit le mode de raccordement à la terre du point neutre d un transformateur de… …   Wikipédia en Français

  • Schémas de mats — Tableau de mat Cet article contient une liste des tableaux de mat typiques du jeu d échecs. Sommaire 1 Baiser de la mort 2 Mat à l étouffée 3 Mat d Anastasie 4 Mat d Anderssen …   Wikipédia en Français

  • Glossaire De La Boxe Et Des Boxes Pieds-Poings — Glossaire de la boxe Nous présentons ici un recueil de termes techniques des boxes modernes dites « sportives » associés à leurs définitions. La définition du mot est la plupart du temps donnée dans le contexte dans lequel il est… …   Wikipédia en Français

  • Glossaire de la boxe et des boxes pieds-poings — Glossaire de la boxe Nous présentons ici un recueil de termes techniques des boxes modernes dites « sportives » associés à leurs définitions. La définition du mot est la plupart du temps donnée dans le contexte dans lequel il est… …   Wikipédia en Français

  • Termes de la boxe et des boxes pieds-poings — Glossaire de la boxe Nous présentons ici un recueil de termes techniques des boxes modernes dites « sportives » associés à leurs définitions. La définition du mot est la plupart du temps donnée dans le contexte dans lequel il est… …   Wikipédia en Français

  • Terminologie de la boxe et des boxes pieds-poings — Glossaire de la boxe Nous présentons ici un recueil de termes techniques des boxes modernes dites « sportives » associés à leurs définitions. La définition du mot est la plupart du temps donnée dans le contexte dans lequel il est… …   Wikipédia en Français

  • Théorie des mécanismes — Pour les articles homonymes, voir Théorie des mécanismes (homonymie). On entend par théorie des mécanismes[1] un ensemble de méthodes qui permettent d étudier les mécanismes et les structures, en vue de les comprendre, de les améliorer ou de les… …   Wikipédia en Français

  • Méthode des différences finies — En analyse numérique, la méthode des différences finies est une technique courante de recherche de solutions approchées d équations aux dérivées partielles qui consiste à résoudre un système de relations (schéma numérique) liant les valeurs des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”