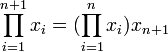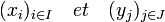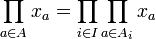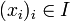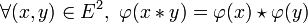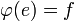Catégorie des monoïdes

Monoïde

En mathématiques, un monoïde est une structure algébrique consistant en un ensemble muni d'une loi de composition interne associative et d'un élément neutre. Un monoïde est donc un magma associatif, c.à.d. un demigroupe, et unifère.

Sommaire

1 Préambule
2 Définition
3 Composé d'une séquence (finie) d'éléments
4 Sous-monoïde
- 4.1 Famille génératrice de sous-monoïde
5 Bases et monoïdes libres
6 Exemples
7 Morphisme de monoïde
8 Produit direct de monoïdes
9 Symétrique d'un élément
10 Itération
11 Applications
12 Bibliographie
13 Notes et références

Préambule

Il arrive parfois qu'une structure composée d'un ensemble et d'une unique opération soit relativement pauvre en propriétés élémentaires, par exemple un anneau où l'on considère uniquement la multiplication. Une telle structure est appelée monoïde. La pauvreté en question rend difficile l'établissement de théorèmes nombreux ou puissants. Pour pallier cette faiblesse, une technique consiste à enrichir le monoïde pour en faire un groupe. Cette méthode est utilisée en théorie algébrique des nombres dans le cas des idéaux de la fermeture intégrale d'un corps de nombre, on travaille alors essentiellement sur le groupe des classes d'idéaux.

Parfois, cette technique ne correspond pas au besoin. Tel est le cas pour l'étude des polynômes en plusieurs indéterminées. On travaille sur un monoïde particulier, engendré par un ensemble d'indices, et on construit une algèbre associative sur le monoïde.

Définition

Formellement, 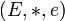$(E, *, e)\,$ est un monoïde lorsque :

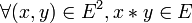$\forall (x,y)\in E^2, x*y \in E$ (stabilité)
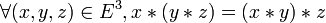$\forall (x,y,z)\in E^3, x*(y*z) = (x*y)*z$ (associativité)
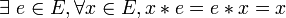$\exists\ e\in E, \forall x\in E, x*e=e*x=x$ (élément neutre)

Un monoïde E est dit simplifiable à gauche, ou encore régulier à gauche, (resp. à droite) si

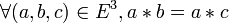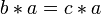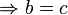$\forall (a,b,c)\in E^3, a*b=a*c\,$ (resp. $b*a=c*a\,$ ) $\Rightarrow b=c$ .

On dit que deux éléments x, y d'un monoïde commutent (l'un avec l'autre) ou sont permutables (l'un avec l'autre) si :

x * y = y * x

Un monoïde est dit commutatif si sa loi de composition est commutative, c'est-à-dire si :

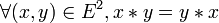$\forall (x,y)\in E^2, x*y = y*x$ ,

ce qui revient à dire que tous les éléments de E commutent l'un avec l'autre.

Composé d'une séquence (finie) d'éléments

Soit E un monoïde. Notons sa loi de composition sous forme multiplicative, c'est-à-dire que nous écrirons xy pour désigner le composé noté 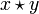$x \star y$ plus haut. L'élément neutre est alors désigné par 1.
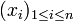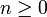Nous nous proposons de définir le composé (« produit » dans notre notation) d'un n-uplet $(x_{i})_{1 \leq i \leq n}$ d'éléments de E, quel que soit le nombre naturel $n \geq 0$ .
Étant donné un tel n-uplet, nous pouvons construire par récurrence sur i un (n+1)-uplet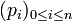 $(p_{i})_{0 \leq i \leq n}$ d'éléments de E en posant :

p 0 = 1

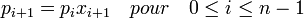$p_{i + 1} = p_{i}x_{i + 1} \quad pour \quad 0 \leq i \leq n - 1$ .

Nous définissons alors le composé du n-uplet 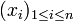$(x_{i})_{1 \leq i \leq n}$ comme étant $p n$ . On note ce composé

$x_{1} \ldots x_{n}$

ou encore

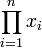$\prod _{i=1}^{n}x_{i}$ .

On montre facilement par récurrence sur i que si 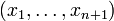$(x_{1}, \ldots ,x_{n+1})$ est un (n+1)-uplet d'éléments de E, les n+1 « produits partiels » $p i$ associés comme ci-dessus au n-uplet (plus petit) 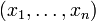$(x_{1}, \ldots ,x_{n})$ sont les n+1 premiers des n+2 produits partiels associés au (n+1)-uplet 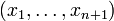$(x_{1}, \ldots ,x_{n+1})$ , d'où la formule

$\prod _{i=1}^{n+1}x_{i} = (\prod _{i=1}^{n}x_{i})x_{n+1}$

qu'on peut encore écrire

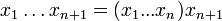$x_{1} \ldots x_{n+1} = (x_{1}...x_{n}) x_{n+1}$ .

Cette formule, ou la formule

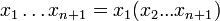$x_{1} \ldots x_{n+1} = x_{1}(x_{2}...x_{n+1})$ ,

est couramment présentée comme définition de 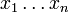$x_{1} \ldots x_{n}$ par récurrence sur n. Du fait de l'associativité, ces deux formules fournissent la même définition. En effet, avec la définition que nous avons choisie, on prouve par récurrence sur s que, pour tous nombres naturels r et s, pour tout r-uplet 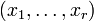$(x_{1}, \ldots , x_{r})$ et tout s-uplet 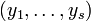$(y_{1}, \ldots , y_{s})$ d'éléments de E,

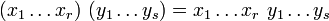$(x_{1} \ldots x_{r}) \ (y_{1} \ldots y_{s}) = x_{1} \ldots x_{r} \ y_{1} \ldots y_{s}$ ,

ce qui permet de prouver l'équivalence des deux définitions par récurrence sur le nombre de facteurs.

D'après ces définitions, le produit de la famille vide (ou 0-uplet) est égal à 1.

On appelle séquence d'éléments de E une famille d'éléments de E indexée par un ensemble fini totalement ordonné. On associe de façon évidente à une telle séquence un n-uplet 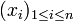$(x_{i})_{1 \leq i \leq n}$ d'éléments de E, ce qui permet d'étendre de façon évidente la définition du composé d'un n-uplet d'éléments de E à toute séquence d'éléments de E. Deux séquences

$(x_{i})_{i \in I} \quad et \quad (y_{j})_{j \in J}$

sont dites équivalentes s'il existe un isomorphisme $σ$ d'ensembles ordonnés de I sur J tel que, pour tout élément i de I,

y σ(i) = x i

Cela équivaut à ce que les n-uplets correspondant à ces deux séquences soient identiques, donc deux séquences équivalentes ont le même composé.

La considération des séquences permet de formuler comme suit le théorème d'associativité^[1] :

Soit E un monoïde, noté multiplicativement, soit A un ensemble fini totalement ordonné, soit 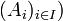$(A_{i})_{i \in I})$ une famille finie de parties deux à deux disjointes de A dont la réunion est A tout entier. (On n'exclut pas que certains des ensembles considérés soient vides.) On suppose que si i et j sont deux éléments de I tels que i < j, alors a < b pour tout élément a de $A i$ et tout élément b de $A j$ . Pour toute séquence 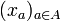$(x_{a})_{a \in A}$ d'éléments de E indexée par A, on a

$\prod _{a \in A}x_{a} = \prod _{i \in I} \prod _{a \in A_{i}}x_{a}$

Si le monoïde E est commutatif, on peut définir le composé d'une famille finie d'éléments de E sans préciser un ordre sur l'index de cette famille, car on prouve que le composé, tel que défini ci-dessus, est alors indépendant de l'ordre choisi. Plus généralement, si E est un monoïde non forcément commutatif, si

$(x_i)_i \in I$

est une famille d'éléments de E dont tous les éléments commutent l'un avec l'autre, le produit des éléments de cette famille ne dépend pas de l'ordre choisi. C'est le « théorème de commutativité »^[2].

Sous-monoïde

Un sous-monoïde d'un monoïde 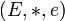$(E,*,e)\,$ est un sous ensemble 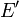$E'\,$ de $E\,$ vérifiant:

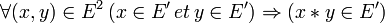$\forall (x,y)\in E^2\, (x \in E'\, et\, y \in E') \Rightarrow (x*y \in E')$ (stable)
$e \in E'\,$

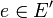
Famille génératrice de sous-monoïde

Soit $P$ une partie d'un monoïde $(E, * , e)$ . On appelle sous-monoïde engendré par $P$ (noté $P *$ ) le plus petit sous-monoïde de $E$ contenant $P$ . Il peut être défini par :

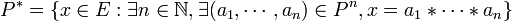
$P^* = \{ x \in E : \exists n \in \N, \exists (a_1,\cdots,a_n) \in P^n, x = a_1 *\cdots * a_n \}$

$P$ est appelé est famille génératrice de $P *$ .

Notons que l'élément $e$ fait bien toujours partie de $P *$ : il admet une décomposition constituée par un produit vide ( $n = 0$ ).

On peut toujours trouver une famille génératrice à tout monoïde, la plus triviale étant lui-même.

Bases et monoïdes libres

Une partie $P$ d'un monoïde $(E, * , e)$ est appelée base de $E$ si c'est une famille génératrice de $E$ dans laquelle tout élément se décompose de façon unique. C'est à dire si

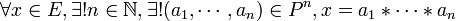
$\forall x \in E, \exists! n \in \N, \exists! (a_1,\cdots,a_n) \in P^n, x = a_1 *\cdots * a_n$

Un monoïde est dit libre s'il admet une base. Dans ce cas, la base est unique.

$e$ n'appartient jamais à la base, sans quoi les éléments auraient une infinité de décomposition possible.

Si $A$ est un ensemble (appelé parfois alphabet), l'ensemble des suites finies d'éléments de $A$ (appelées mots) muni de l'opération de concaténation est un monoïde libre noté $A *$ et appelé monoïde libre sur A. Sa base est l'ensemble des mots de longueur un, et donc assimilable naturellement à l'alphabet.

Deux monoïdes libres sur des alphabets finis sont isomorphes si et seulement si leurs bases ont même cardinal.

Dans un monoïde libre l'élément neutre est le seul élément symétrisable.

Exemples

L'ensemble des entiers naturels, muni de l'addition, est un monoïde, dont 0 est l'élément neutre ;
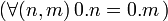L'ensemble des entiers naturels, muni de la multiplication, est un monoïde d'élément neutre 1. 0 n'est pas simplifiable $(\forall (n,m)\, 0.n=0.m\,)$ ;
L'ensemble des parties d'un ensemble E, muni de l'union ensembliste, est un monoïde, dont l'ensemble vide est l'élément neutre. Le même ensemble muni de l'intersection ensembliste est aussi un monoïde dont E est l'élément neutre.
L'ensemble des entiers naturels muni de la loi Max qui a deux entiers associe le plus grand des deux est un monoïde de neutre 0.
La deuxième loi d'un anneau possède une structure de monoïde. Beaucoup de propriétés des anneaux en découlent, notamment l'étude des Anneaux factoriels.

Morphisme de monoïde

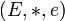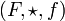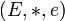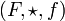Soit $(E,*,e)\,$ et $(F,\star,f)$ deux monoïdes. on appelle morphisme de $(E,*,e)\,$ vers $(F,\star,f)$ toute application $\varphi$ de $E$ vers $F$ telle que

$\forall (x,y)\in E^2,\ \varphi(x*y) =\varphi(x)\star\varphi(y)$
$\varphi(e) =f$

La première propriété est celle de morphisme de loi ou morphisme de magma.

La composée de deux morphismes de monoïde est un morphisme de monoïde.
La réciproque de tout morphisme bijectif de monoïde est un morphisme de monoïde. En conséquence, un morphisme bijectif est qualifié d'isomorphisme.
L'image d'un élément idempotent par un morphisme de monoïde est un élément idempotent.
Si on munit l'ensemble des entiers naturels de la loi Max, l'application 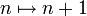$n \mapsto n+1$ est un morphisme de loi mais n'est pas un morphisme de monoïde.
Tout morphisme de loi d'un monoïde vers un groupe est un morphisme de monoïde.
L'image d'un sous-monoïde par un morphisme de monoïde est un sous-monoïde. En particulier l'image d'un morphisme de monoïde est un sous-monoïde.

On appelle noyau d'un morphisme de monoïde l'ensemble des antécédents de l'élément neutre.

Attention, il n'y a pas de lien clair entre noyau et injectivité lorsque le monoïde n'est pas un groupe. Par exemple, l'application 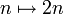$n \mapsto 2n$ est un endomorphisme du monoïde des entiers naturels muni de la loi Max.

L'image réciproque d'un sous-monoïde par un sous-monoïde est un sous-monoïde. En particulier le noyau d'un morphisme de monoïde est un sous-monoïde.

Produit direct de monoïdes

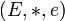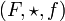Soit $(E,*,e)\,$ et $(F,\star,f)\,$ deux monoïdes. on peut munir le produit cartésien et 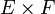$E\times F\,$ d'une structure de monoïde en introduisant une nouvelle loi $\wedge$ de la façon suivante :

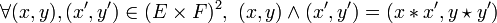$\forall (x,y),(x',y') \in (E\times F)^2,\ (x,y)\wedge (x',y')= (x*x',y\star y')$ .

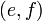
C'est un monoïde de neutre $\displaystyle (e,f)$

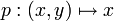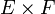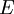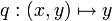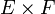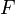Les deux projections $p : (x,y) \mapsto x$ de $E\times F$ dans $\displaystyle E$ et $q : (x,y) \mapsto y$ de $E\times F$ dans $\displaystyle F$ sont des morphismes de monoïde. Et le triplet 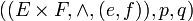$((E\times F,\wedge,(e,f)),p,q)$ vérifie la propriété universelle du produit direct.

Plus généralement, soit $I$ un ensemble et 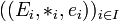$((E_i,*_i,e_i))_{i\in I}$ une famille de monoïde. On construit la structure de produit direct sur le produit cartésien 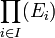$\prod_{i\in I}(E_i)$ par la formule

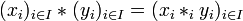$(x_i)_{i\in I} * (y_i)_{i\in I} = (x_i *_i y_i)_{i\in I}$ .

Symétrique d'un élément

Article détaillé : élément symétrique.

Soit $(E, * , e)$ un monoïde et soit $x$ un élément de $E$ . On dira que

$x$ est symétrisable à droite si et seulement s'il existe un élément $y$ dans $E$ tel que $x * y = e$ . On dit alors que $y$ est un symétrique à droite de $x$ .
$x$ est symétrisable à gauche si et seulement s'il existe un élément $z$ dans $E$ tel que $z * x = e$ . On dit alors que $z$ est un symétrique à gauche de $x$ .
$x$ est symétrisable si et seulement si $x$ est symétrisable à droite et à gauche.

Lorsque $x$ est symétrisable il admet un unique symétrique à droite et un unique symétrique à gauche et ceux-ci sont égaux. Cet unique élément est appelé symétrique de $x$ .

En effet, c'est une conséquence de l'associativité, avec les notations ci-dessus $y = e * y = (z * x) * y = z * (x * y) = z * e = z$

Le symétrique de $x$ est généralement noté $x - 1$ . On le note parfois $\frac1x$ lorsque la loi est commutative, c'est notamment le cas avec la multiplication des nombres réels. On le note $- x$ lorsque la loi du monoïde est notée $+$ .

Le symétrique est souvent appelé inverse, c'est notamment le cas pour les multiplications. Le symétrique pour les additions est appelé opposé.

Si $x$ et $y$ sont symétrisables, il en est de même de $x * y$ et on a $(x * y) - 1 = y - 1 * x - 1$ .

On vérifie $(x * y) * (y - 1 * x - 1) = x * (y * y - 1) * x - 1 = x * e * x - 1 = x * x - 1 = e$ grâce à l'associativité et on fait de même à gauche.

L'ensemble des éléments symétrisables d'un monoïde forme un groupe.

Itération

Article détaillé : itération.

Le monoïde est un cadre propice pour définir les itérations d'un élément.

Applications

En mathématiques, il est rare d'utiliser les monoïdes ; car souvent, lorsqu'une structure est trop pauvre en termes de propriétés pour pouvoir continuer son étude, elle se trouve plongée dans une structure plus riche, comme les groupes, ou les anneaux... Les entiers naturels en sont un exemple frappant : pour les étudier, on étudie les entiers relatifs, qui eux forment un groupe, et mieux, un anneau factoriel !

En informatique théorique, les monoïdes et plus particulièrement le monoïde libre sont parmi les structures les plus utilisées, notamment dans la théorie des codes et dans la théorie des langages.

Bibliographie

A.H. Clifford et G.B. Preston, The algebraic theory of semigroups, American Mathematical Society, vol. 1 (2^e éd. 1964) et vol. 2 (réimpr. 1988).

Notes et références

↑ N. Bourbaki, Algèbre, Paris, Hermann, 1970, ch. I, § 1, n° 3, p. 4, et § 2, n° 1, p. 13.
↑ N. Bourbaki, Algèbre, ch. I, § 1, théor. 2, Paris, 1970, p. 8.

Portail des mathématiques

Ce document provient de « Mono%C3%AFde ».

Catégorie : Structure algébrique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Catégorie des monoïdes de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Catégorie (mathématiques) — Théorie des catégories La théorie des catégories étudie les structures mathématiques et les relations qu elles entretiennent. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l informatique… … Wikipédia en Français
Théorie des catégories — La théorie des catégories étudie les structures mathématiques et les relations qu elles entretiennent. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l informatique théorique et en… … Wikipédia en Français
Theorie des categories — Théorie des catégories La théorie des catégories étudie les structures mathématiques et les relations qu elles entretiennent. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l informatique… … Wikipédia en Français
Produit (catégorie) — Dans une catégorie, le produit peut s exprimer par une propriété universelle ou de manière équivalente comme foncteur représentable. Définition produit Soit C une catégorie et une famille d objets de C. On cherche un objet X ainsi qu une famille… … Wikipédia en Français
Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces … Wikipédia en Français
Algèbre d'un monoïde — Pour les articles homonymes, voir Algèbre (homonymie). En algèbre, plus précisément en théorie des anneaux, l algèbre d un monoïde M sur un anneau commutatif A est la A algèbre formée des combinaisons linéaires d éléments de M, à coefficients… … Wikipédia en Français
Algebre universelle — Algèbre universelle L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de… … Wikipédia en Français
Algèbre Universelle — L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de définir de manière… … Wikipédia en Français
Limite projective — En mathématiques, formalisée dans le langage des catégories, la limite projective est une généralisation du produit. Cette notion est duale de celle de limite inductive. Sommaire 1 Limite projective d ensembles 2 Système projectif … Wikipédia en Français
Foncteur — En mathématiques, le foncteur est la généralisation aux catégories de la notion de morphisme. Sommaire 1 Définitions 1.1 Foncteurs adjoints 2 Exemples 3 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Catégorie des monoïdes

Monoïde

Sommaire

Préambule

Définition

Composé d'une séquence (finie) d'éléments

Sous-monoïde

Famille génératrice de sous-monoïde

Bases et monoïdes libres

Exemples

Morphisme de monoïde

Produit direct de monoïdes

Symétrique d'un élément

Itération

Applications

Bibliographie

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Catégorie des monoïdes

Monoïde

Sommaire

Préambule

Définition

Composé d'une séquence (finie) d'éléments

Sous-monoïde

Famille génératrice de sous-monoïde

Bases et monoïdes libres

Exemples

Morphisme de monoïde

Produit direct de monoïdes

Symétrique d'un élément

Itération

Applications

Bibliographie

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link