Théorème des quatre sommets

Théorème des quatre sommets
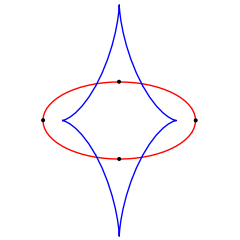Une ellipse (en rouge) et sa développée (en bleu), montrant les 4 sommets annulant k', chacun d'eux correspondant à un point de rebroussement de la développée.

Le théorème des quatre sommets constitue un résultat remarquable de géométrie différentielle quant aux propriétés globales des courbes fermées.

Sommaire

Énoncé dans le cas le plus simple

Soit γ une courbe fermée convexe, paramétrée par sa longueur s. Soit k(s) la courbure calculée au point γ(s). Alors il existe au moins quatre valeurs si du paramètre s pour lesquelles k'(si) = 0.

La signification géométrique de ce résultat est que soit la courbure est constante, soit elle possède au moins quatre extrema. On pourra en trouver une démonstration dans (do Carmo 1976).

Cas général

Adolf Kneser a démontré le cas général en 1912.

Le théorème des quatre sommets a d'abord été démontré pour les courbes convexes (c'est-à-dire à courbure strictement positive) en 1909 par Syamadas Mukhopadhyaya[1]. Sa preuve utilise le fait qu'un point de la courbe est un extremum de la fonction courbure si et seulement si en ce point, le cercle osculateur possède un contact d'ordre 4 avec la courbe (en un point ordinaire, le contact est seulement d'ordre 3). Le théorème des quatre sommets a été démontré dans le cas général par Adolf Kneser (de) en 1912, par un argument de géométrie projective[2].

Réciproque

La réciproque du théorème des quatre sommets énonce que si une application continue d'un cercle dans R possède deux maxima locaux et deux minima locaux, alors cette application est la courbure d'une courbe simple et fermée du plan. Cette réciproque a été prouvée pour des fonctions strictement positives en 1971 par Herman Gluck, en tant que cas particulier d'un théorème plus général sur l'existence d'une hypersurface, paramétrée par une hypersphère, à courbure prescrite[3]. La réciproque a été finalement démontrée dans le cas général par Björn Dahlberg peu de temps avant sa mort en janvier 1998 et publiée à titre posthume[4]. La preuve de Dahlberg utilise principalement l'indice, argument qui rappelle celui de la démonstration homotopique du théorème de d'Alembert-Gauss.

Notes et références

  1. ↑ (en) S. Mukhopadhyaya, « New methods in the geometry of a plane arc », dans Bull. Calcutta Math. Soc., vol. 1, 1909, p. 21-27 
  2. ↑ (de) Adolf Kneser, « Bemerkungen über die Anzahl der Extrema des Krümmung auf geschlossenen Kurven und über verwandte Fragen in einer nicht eucklidischen Geometrie », dans Festschrift Heinrich Weber, Teubner, 1912, p. 170-180 
  3. ↑ (en) Herman Gluck, « The converse to the four-vertex theorem », dans L'Enseignement Math., vol. 17, 1971, p. 295-309 
  4. ↑ (en) Björn Dahlberg, « The converse of the four vertex theorem », dans Proc. Amer. Math. Soc., vol. 133, no 7, 2005, p. 2131-2135 [texte intégral [PDF]] 

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème des quatre sommets de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Theoreme des quatre sommets — Théorème des quatre sommets Une ellipse (en rouge) et sa développée (en bleu), montrant les 4 sommets annulant k , chacun d eux correspondant à un cusp de la développée. Le théorème des 4 sommets consititue un résultat remarquable de géométrie… …   Wikipédia en Français

  • Theoreme des quatre couleurs — Théorème des quatre couleurs Carte administrative de la Russie colorée avec quatre couleurs Le théorème des quatre couleurs affirme qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] …   Wikipédia en Français

  • Théorème des quatre couleurs — Vitrail coloré avec quatre couleurs Le théorème des quatre couleurs indique qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] n importe quelle carte découpée en régions connexes, de sorte que deux régions… …   Wikipédia en Français

  • Problème des quatre couleurs — Théorème des quatre couleurs Carte administrative de la Russie colorée avec quatre couleurs Le théorème des quatre couleurs affirme qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] …   Wikipédia en Français

  • Théorème de carathéodory (géométrie) — Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé 2 Preuves 2.1 La preuve usuelle …   Wikipédia en Français

  • Théorème de Helly — dans le plan : si trois quelconques des convexes de la famille se rencontrent alors l intersection de tous ces convexes est non vide. Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par… …   Wikipédia en Français

  • Théorème de helly — Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par Eduard Helly, et il a été publié par Johann Radon en 1921[1],[2]. Énoncé Théorème …   Wikipédia en Français

  • Theoreme de Krein-Milman — Théorème de Krein Milman Le théorème de Krein Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par …   Wikipédia en Français

  • Théorème de krein-milman — Le théorème de Krein Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par Hermann Minkowski en… …   Wikipédia en Français

  • Théorème de Radon (Géométrie) — Sommaire 1 Énoncé 2 Preuve 3 Théorème de Tverberg 4 Notes et références // …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”