Indice (analyse complexe)

Indice (analyse complexe)
Page d'aide sur l'homonymie Pour les articles homonymes, voir indice.
Un point z0 et une courbe C

Indice d'un point par rapport à un lacet

La définition la plus générale de l'indice (qui permet de définir l'indice d'un lacet dans le cas "continu" et pas seulement dans le cas "différentiable par morceaux") utilise la propriété de relèvement des chemins dans le revêtement universel réalisé par l'exponentielle complexe.

Si \gamma: [a,b] \rightarrow \mathbb{C}^{*} est un lacet (chemin continu tel que γ(a) = γ(b)) dans le plan complexe privé de l'origine, il existe un relèvement (non unique) {\tilde{\gamma}}: [a,b] \rightarrow \mathbb{C} de γ à travers l'exponentielle complexe, c'est-à-dire un chemin \tilde{\gamma}: [a,b] \rightarrow \mathbb{C} tel que \gamma = e^{\tilde{\gamma}}. La quantité

\frac{1}{2\mathrm{i}\pi} (\tilde{\gamma}(b) - \tilde{\gamma}(a))

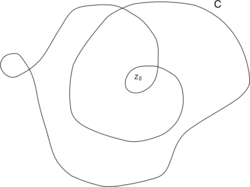
ne dépend pas du relèvement \tilde{\gamma} choisi et s'appelle l'indice de γ par rapport à 0; elle correspond au "nombre de tours" comptés algébriquement (c'est-à-dire en tenant compte du sens de parcours) que fait le lacet autour de l'origine. En effet, \tilde{\gamma}: [a,b] \rightarrow \mathbb{C} apparaît comme un "logarithme" du lacet γ et donc (\tilde{\gamma}(b) - \tilde{\gamma}(a)) correspond à la différence des valeurs de la partie imaginaire du logarithme complexe, c'est-à-dire une fonction argument.

Si maintenant \gamma: [a,b] \rightarrow \mathbb{C} est un lacet quelconque et z un nombre complexe n'appartenant pas à l'image \gamma([a,b]) \subset \mathbb{C} de γ , l'indice de z par rapport à γ, noté \operatorname{Ind}_{\gamma} (z), est l'indice par rapport à 0 du lacet γ − z. Cette définition de l'indice fait clairement apparaître cette quantité comme un cas particulier du degré de l'application de Gauss en topologie.

Lorsque que le lacet γ est différentiable par morceaux, l'indice s'exprime sous forme d'une intégrale:

\operatorname{Ind}_{\gamma} (z) =\frac{1}{2 \mathrm{i} \pi} \int_{\gamma} \frac{\mathrm d \zeta}{\zeta - z} \; .

Propriétés

En notant \Omega = \mathbb{C} \smallsetminus \gamma([a,b])), on a que z \rightarrow \operatorname{Ind}_{\gamma} (z) est une fonction à valeurs entières sur Ω, constante sur les composantes connexes de Ω, et nulle sur la composante non bornée de Ω. Ces valeurs entières correspondent au nombre de tours effectués par le lacet autour du point z.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Indice (analyse complexe) de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Indice(analyse complexe) — Indice (analyse complexe) Pour les articles homonymes, voir indice. Un point z0 et une courbe C …   Wikipédia en Français

  • Zéro (analyse complexe) — Zéro d une fonction holomorphe En analyse complexe, on appelle zéro d une fonction analytique ou holomorphe f un nombre complexe a tel que f(a) = 0. Sommaire 1 Ordre de multiplicité d un zéro isolé 1.1 Théorème et définition …   Wikipédia en Français

  • Residu (analyse complexe) — Résidu (analyse complexe) En analyse complexe, le résidu est un nombre complexe qui décrit le comportement de l intégrale curviligne d une fonction holomorphe aux alentours d une singularité. Les résidus se calculent assez facilement et, une fois …   Wikipédia en Français

  • Résidu (analyse complexe) — En analyse complexe, le résidu est un nombre complexe qui décrit le comportement de l intégrale curviligne d une fonction holomorphe aux alentours d une singularité. Les résidus se calculent assez facilement et, une fois connus, permettent de… …   Wikipédia en Français

  • Singularité en analyse complexe — En analyse complexe à une variable, une singularité d une fonction f est un point z au voisinage épointé duquel la fonction f est définie et holomorphe. Autrement dit, on dispose d une fonction f d une variable complexe régulière (= holomorphe)… …   Wikipédia en Français

  • Indice d'un lacet — Lacet (mathématiques) En mathématiques, un lacet est la modélisation d une « boucle ». C est une courbe continue et fermée, c est à dire que ses extrémités sont confondues. La notion de lacet est utile en analyse complexe et en… …   Wikipédia en Français

  • Indice — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Indice », sur le Wiktionnaire (dictionnaire universel) Le mot indice peut avoir plusieurs… …   Wikipédia en Français

  • Analyse Harmonique Sur Un Groupe Abélien Fini — En mathématiques, l analyse harmonique sur un groupe abélien fini est un cas particulier d analyse harmonique correspondant au cas où le groupe est abélien et fini. L analyse harmonique permet de définir la notion de transformée de Fourier ou le… …   Wikipédia en Français

  • Analyse harmonique sur un groupe abelien fini — Analyse harmonique sur un groupe abélien fini En mathématiques, l analyse harmonique sur un groupe abélien fini est un cas particulier d analyse harmonique correspondant au cas où le groupe est abélien et fini. L analyse harmonique permet de… …   Wikipédia en Français

  • Indice de sévérité de la sécheresse de Palmer — Indice de sècheresse de Palmer L’indice de sècheresse de Palmer, parfois appelé indice de sévérité de la sécheresse de Palmer et souvent abrégé en PDSI (de l anglais Palmer Drought Severity Index), est une mesure de la sècheresse fondée sur les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”