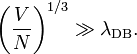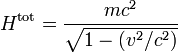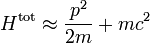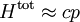- Theoreme d'equipartition
-
Équipartition de l'énergie
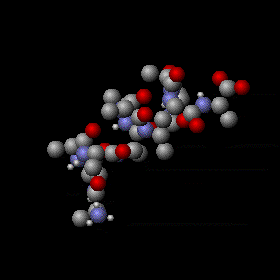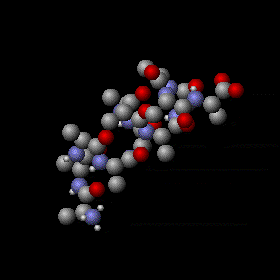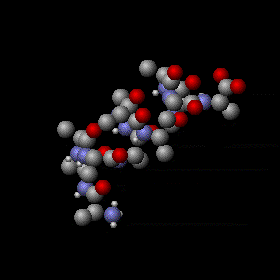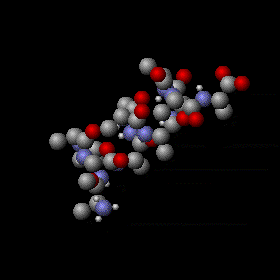 Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer l’énergie cinétique moyenne de chaque atome ainsi que l’énergie potentielle moyenne de nombreux modes de vibration. Les sphères grises, rouges et bleues représentent des atomes de carbone, d’oxygène et d’azote respectivement. Les sphères blanches plus petites représentent des atomes d’hydrogène.
Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer l’énergie cinétique moyenne de chaque atome ainsi que l’énergie potentielle moyenne de nombreux modes de vibration. Les sphères grises, rouges et bleues représentent des atomes de carbone, d’oxygène et d’azote respectivement. Les sphères blanches plus petites représentent des atomes d’hydrogène.
En physique statistique classique, l’équipartition de l’énergie est un résultat remarquable selon lequel l’énergie totale d’un système à l’équilibre thermodynamique est répartie en parts égales en moyenne entre ses différentes composantes. Ce résultat découle très directement du postulat fondamental de la physique statistique ; on parle souvent de principe d’équipartition de l’énergie.
Plus précisément, le théorème d’équipartition donne une équation qui permet de relier la température d’un système macroscopique aux énergies moyennes des particules microscopiques qui le composent, permettant ainsi de faire des prédictions quantitatives. On le résume souvent par la formule : 1/2 kBT par degré de liberté, où kB est la constante de Boltzmann et T la température exprimée en kelvin. Le théorème permet de calculer l’énergie totale d’un système à une température donnée, d’où l’on peut calculer sa chaleur spécifique. Mais il donne aussi les valeurs moyennes de composantes de l’énergie, telles que l’énergie cinétique d’une particule ou l’énergie potentielle associée à un mode de vibration particulier.
Le théorème d’équipartition peut notamment être utilisé pour retrouver la loi des gaz parfaits, la loi expérimentale de Dulong et Petit sur la chaleur spécifique des solides ou caractériser un mouvement brownien. De manière générale, il peut être appliqué à n’importe quel système classique à l’équilibre thermodynamique, quelle que soit sa complexité. En revanche, il est mis en défaut quand les effets quantiques deviennent significatifs, notamment pour des températures suffisamment basses ou des densités élevées.
Historiquement, le problème de l’équipartition de l’énergie est lié à d’importants développements en physique et en mathématiques. Il a trouvé son origine au milieu du XIXe siècle dans la théorie cinétique des gaz, puis accompagné l’émergence de la physique statistique. Au début du XXe siècle, il était encore au cœur de problèmes fondamentaux, dont notamment la catastrophe ultraviolette, qui ont conduit au développement de la mécanique quantique. En mathématiques, l’examen des conditions de validité du principe d’équipartition a donné naissance à la théorie ergodique, une branche dans laquelle de nombreux problèmes restent encore ouverts.
Sommaire
Historique
Premières formulations
L’équipartition de l’énergie cinétique fut initialement proposée en 1843[1] par John James Waterston qui travaillait à une première théorie cinétique des gaz. À cette époque, Waterston était aux Indes où il travaillait en tant qu’ingénieur pour le développement du chemin de fer. Il proposa son mémoire en 1845 à la Royal Society qui refusa de le publier, mais le conserva dans ses archives. Un court résumé de ses idées fut publié en 1846, puis un autre en 1851 dans laquelle on trouve une première version du principe d’équipartition de l’énergie. Le mémoire d’origine fut redécouvert et finalement publié bien plus tard en 1893, assorti d’une introduction de Lord Rayleigh qui critique vivement le refus initial en reconnaissant l’antériorité du travail de Waterston (mais aussi certaines erreurs)[2]. Telle que publiée en 1851, cette première version du principe d’équipartition s’écrit :
Ces premiers travaux sont donc inconnus des principaux physiciens de l’époque qui développeront pendant les vingt ans qui suivirent la théorie cinétique des gaz et affineront les arguments, les formulations et les démonstrations du principe d’équipartition. Rudolf Clausius, Ludwig Boltzmann, James Clerk Maxwell sont de ceux-là. Ce dernier écrit notamment en 1878[4] :
« À une température donnée, l’énergie cinétique totale d’un système matériel est égale au produit du nombre de degrés de liberté de ce système par une constante qui est la même pour toute substance à cette température, cette constante étant en fait la température de l’échelle thermodynamique multipliée par une constante absolue[5]. »Le théorème d’équipartition est considéré pendant le dernier tiers du XIXe siècle comme un des résultats principaux de la théorie cinétique des gaz. Sa généralité et sa simplicité en font un résultat séduisant ; il est connu et utilisé couramment par les expérimentateurs[6].
Un grand succès du théorème d’équipartition fut la prédiction par Boltzmann de la loi expérimentale de Dulong et Petit sur la chaleur spécifique des solides, autre sujet d’étude au XIXe siècle. En 1819 en effet, les physiciens français Pierre Louis Dulong et Alexis Thérèse Petit avaient découvert que les chaleurs spécifiques molaires des solides à température ambiante étaient quasiment toutes identiques, environ 6 cal/(mol·K)[7]. Cette loi jusqu’alors expérimentale trouva dans le théorème d’équipartition un fondement théorique. De même, les mesures des chaleurs spécifiques de gaz monoatomiques étaient tout à fait conformes à la théorie. Le théorème prédit que la chaleur spécifique d’un gaz simple monoatomique doit être d’environ 3 cal/(mol·K), ce qui fut en effet confirmé par l’expérience[8].
Paradoxes théoriques et expérimentaux
Cependant, le théorème d’équipartition fut également mis en défaut. Dès 1840, des mesures de chaleur spécifique de solides avaient mis en évidence des écarts significatifs avec la loi de Dulong et Petit, notamment dans le cas du diamant[9],[10]. Au début des années 1870, des études en fonction de la température par James Dewar[11] et Heinrich Friedrich Weber[12],[13] montrèrent que la loi de Dulong et Petit n’était en réalité valable que pour les hautes températures.
Des mesures de chaleurs spécifiques de gaz diatomiques vinrent également contredire le théorème d’équipartition. Le théorème prédisait une valeur de 7 cal/(mol·K) quand les chaleurs spécifiques mesurées étaient typiquement proches de 5 cal/(mol·K)[14] et tombaient même jusqu’à 3 cal/(mol·K) aux très basses températures[15].
Une troisième cas de désaccord fut la chaleur spécifique des métaux[16]. Selon le classique modèle de Drude développé au début des années 1900 et le théorème d’équipartition, les électrons dans les métaux devraient se comporter comme un gaz quasi parfait, et devraient contribuer pour 3/2 NekB à la chaleur spécifique où Ne est le nombre d’électrons. L’expérience montre toutefois que les électrons contribuent peu à la chaleur spécifique : les chaleurs spécifiques molaires de nombreux conducteurs et d’isolants sont quasiment égales[16].
Un dernier cas de désaccord, et pas des moindres, était donné par le problème de l’émission de rayonnement du corps noir. Le paradoxe vient du fait qu’il y a une infinité de modes indépendants du champ électromagnétique dans une cavité fermée, chacun pouvant être traité comme un oscillateur harmonique. Si chaque mode avait une énergie kBT, la cavité contiendrait donc une énergie infinie[17],[18]. Ce paradoxe est resté dans l’histoire sous le nom de catastrophe ultraviolette. En 1900, ce paradoxe est le second « nuage » évoqué par Lord Kelvin lors de sa conférence Nineteenth-Century Clouds over the Dynamical Theory of Heat and Light[19]. Il ne sera résolu que par les développements de mécanique quantique.
Au-delà des cas d’échecs rapportés par l’expérience, le théorème d’équipartition se heurte également à un problème fondamental, souligné dès 1875 par James Maxwell[20] : à mesure que l’on décompose les molécules de gaz en constituants élémentaires, on peut trouver de nouveaux degrés de libertés qui devraient aux-aussi contribuer à l’énergie totale. À la limite, celle-ci deviendrait infinie ! Ce paradoxe est insoluble par la physique classique. Et pourtant, la démonstration du théorème ne présente pas de faille apparente, et les succès de la théorie cinétique des gaz sont par ailleurs indéniables.
Face à ces difficultés, plusieurs attitudes sont possibles. Certains, mais pas les plus nombreux, pensent que le théorème est faux. C’est notamment le cas de Lord Kelvin[21]. Mais ils ne parviennent pas à démontrer en quoi. D’autres, prenant actes des succès du théorème, préfèrent penser qu’il n’est pas applicable dans les cas qui posent problèmes, pour des raisons qui restent à préciser. Ludwig Boltzmann avança que les gaz pouvaient ne pas être à l’équilibre thermodynamique à cause de leurs interactions avec l’éther[22]. Maxwell pense que le problème ne pourra pas être résolu sans une connaissance précise et complète de la structure interne des molécules. Mais ce problème aussi se révèle de plus en plus compliqué. Certains, plus prudents encore, remettent en cause la pertinence de l’utilisation des lois de la mécanique (chocs) aux molécules et, de là, la nature même de la matière. Lord Rayleigh quant à lui, dans une conférence qu’il donne en 1900, avance fermement que le théorème d’équipartition et l’hypothèse expérimentale de l’équilibre thermodynamique sont tous les deux corrects, mais pour les réconcilier invoque le besoin d’un nouveau principe qui pourrait fournir une « échappatoire à la simplicité destructrice » du théorème d’équipartition[23].
Naissance de la mécanique quantique
Cette échappatoire fut trouvée progressivement à partir des années 1900. Cette année-là, Max Planck présente un travail sur le rayonnement du corps noir dans lequel il imagine des niveaux d’énergie discrets, ce qui lui permet d’échapper à la catastrophe ultraviolette. C’est alors une hypothèse purement mathématique. Max Planck ne s’intéresse que peu alors au problème de l’équipartition de l’énergie ; il est réticent de manière générale devant les méthodes de la physique statistique[24].
C’est notamment à Albert Einstein que l’on doit le lien avec l’équipartition[25]. Il insiste en 1905 sur le fait que le théorème d’équipartition associé aux théories classiques du rayonnement conduisent nécessairement à la loi de Rayleigh-Jeans et à la catastrophe ultraviolette[17]. Il introduit en 1907 un effet de quantification pour résoudre le problème de la chaleur spécifique des solides : c’est le modèle d’Einstein qui sera par la suite amélioré par Peter Debye[26]. Au premier congrès Solvay en 1911, il remet en cause la validité du théorème pour les systèmes dont l’énergie est quantifiée.
Mécanique quantique et équipartition semblent alors incompatibles. L’articulation entre les deux sera trouvée avec la théorie quantique du gaz parfait. Dans un article qu’il publie en 1924 en partant des idées de Satyendranath Bose, Einstein montre que l’équipartition est valable dans la limite des faibles densités et des hautes températures, calculant même un critère de validité. Le théorème d’équipartition perd alors définitivement son statut de formule générale pour devenir une approximation, valable seulement quand la physique classique elle-même est une bonne approximation de la physique quantique[27].
Vers la théorie ergodique
Avec le développement de la physique statistique, les conditions de validité de l’équipartition de l’énergie sont clairement posées. Elle repose notamment sur l’hypothèse fondamentale selon laquelle la valeur moyenne d’une grandeur prise sur une durée suffisamment longue (celle que l’on mesure) est égale à la valeur moyenne d’ensemble, calculée par la physique statistique. Cette hypothèse d’ergodicité, formulée explicitement par Boltzmann dès 1871, est validée a posteriori par la justesse des prédictions qu’elle permet, mais reste une hypothèse.
Or, il existe très peu de systèmes pour lesquelles on a la certitude que cette hypothèse est effectivement réalisée. On a même la certitude que cette hypothèse n’est pas réalisée dans un certain nombre de cas très simples : par exemple, un gaz rigoureusement parfait dans lequel les molécules ne s’entrechoqueraient pas n’est pas un système ergodique. Les conditions de validité de cette hypothèse restent à explorer.
En 1953, l’expérience de Fermi-Pasta-Ulam rapporte un exemple d’échec de l’équipartition. Cette première expérience numérique consiste à étudier la répartition à long terme de l’énergie d’un système dynamique unidimensionnel de 64 masses couplées entre elles par des ressorts harmoniques perturbés par une faible anharmonicité, sachant qu’un seul mode du système est initialement excité. L’issue de l’expérience surprend : l’énergie ne se répartit pas également entre les différents modes, contrairement aux prédictions de l’équipartition.
Une première réponse à ce paradoxe sera suggérée par Kolmogorov en 1954, puis démontrée indépendamment par Arnold et Mauser en 1963 : c’est le théorème KAM qui montre que de faibles couplages non linéaires ne suffisent pas à rendre un système ergodique.
Ces travaux ont conduit au développement d’une branche des mathématiques, la théorie ergodique, qui étudie les conditions d’ergodicité d’un système. De nombreux cas d’échec de l’équipartition ont été mis en évidence, souvent au moyen de simulations numériques (chaînes anharmoniques, milieux granulaires…). Dans ce domaine, de nombreux problèmes restent ouverts.
Première approche
Dans une première approche, on résume souvent[28] le théorème d’équipartition de la façon suivante :
Dans un système à l’équilibre à la température T, chaque degré de liberté contribue pour 1/2 kBT à l’énergie totale, où kB est la constante de Boltzmann. Cet énoncé n’est qu’un résultat particulier du théorème. Il omet certaines hypothèses. Cependant, il permet déjà de retrouver un certain nombre de résultats et de traiter des cas particuliers importants qui sont détaillés ci-dessous. Bien entendu, on retrouve dans cette affirmation le fait que l’énergie est répartie également entre tous les degrés de liberté, d’où le nom « équipartition ».
Dans la suite, le symbole H, pour Hamiltonien, sera utilisé comme symbole pour l’énergie en raison du rôle central que joue le formalisme de Hamilton dans la formulation plus générale du théorème d’équipartition qui suivra. D’autre part, on notera avec des crochets
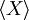 la valeur moyenne d’une quantité X. On en précisera par la suite le sens mathématique précis.
la valeur moyenne d’une quantité X. On en précisera par la suite le sens mathématique précis.Gaz parfait monoatomique : l’exemple des gaz rares
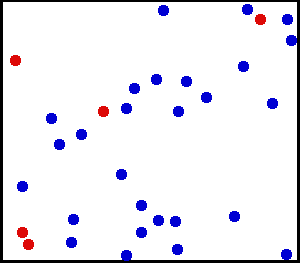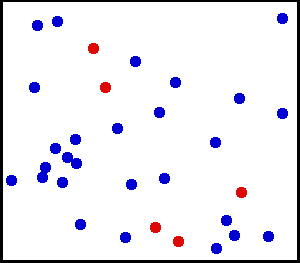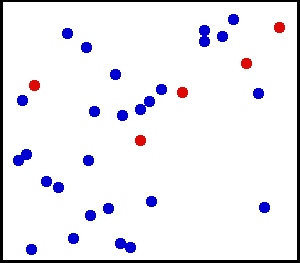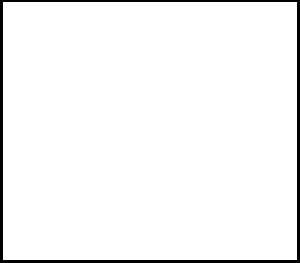 Les gaz rares sont des exemples types pour l’application du théorème d’équipartition. Comme on le voit sur cette simulation, la vitesse, et donc l’énergie cinétique d’un atome donné, peut fluctuer considérablement. Le théorème d’équipartition permet de calculer son énergie cinétique moyenne à une température donnée. Dans ce schéma, cinq particules ont été colorées en rouge afin de suivre plus facilement leur mouvement. La couleur n’a pas d’autre signification.
Les gaz rares sont des exemples types pour l’application du théorème d’équipartition. Comme on le voit sur cette simulation, la vitesse, et donc l’énergie cinétique d’un atome donné, peut fluctuer considérablement. Le théorème d’équipartition permet de calculer son énergie cinétique moyenne à une température donnée. Dans ce schéma, cinq particules ont été colorées en rouge afin de suivre plus facilement leur mouvement. La couleur n’a pas d’autre signification.Un gaz rare est un gaz des plus simples qui soient : il est constitué uniquement d’atomes dont l’énergie n’est donc composée que de l’énergie cinétique due à leur mouvement de translation. Chaque atome dispose de trois degrés de liberté associés aux trois composantes de la vitesse, c’est-à-dire aux trois directions de l’espace. Si on décompose la vitesse de l’atome suivant ces trois directions en les notant vx, vy et vz, en notant m la masse, alors l’énergie cinétique (newtonienne) s’écrit comme une somme de trois termes dont chacun correspond à un degré de liberté :
À l’équilibre thermodynamique, chaque degré de liberté contribue d’après le théorème d’équipartition pour 1/2 kBT à l’énergie cinétique. L’énergie cinétique moyenne totale d’une particule est donc 3/2 kBT, et l’énergie totale d’un gaz parfait composé de N particules est 3/2 NkBT.
Il s’en suit que la chaleur spécifique du gaz est 3/2 NkB et donc en particulier que la chaleur spécifique d’une mole d’un tel gaz est 3/2 NAkB où NA est le nombre d’Avogadro, ou encore 3/2 R où R est la constante des gaz parfaits. Puisque R vaut approximativement 2 cal/(mol.K), le théorème prédit que la capacité thermique molaire d’un gaz parfait est environ 3 cal/(mol.K).
Connaissant l’énergie cinétique moyenne, on peut calculer la vitesse quadratique moyenne vqm des atomes du gaz :
où M = mNA est la masse d’une mole de gaz. La vitesse quadratique moyenne est donc d’autant plus faible que les atomes sont lourds. Les atomes du xénon auront une vitesse moyenne plus basse que les atomes plus légers de l’hélium à une même température. Ce résultat est utile dans un grand nombre d’applications, telles que la loi d’effusion de Graham dont a été tirée notamment une méthode d’enrichissement de l’uranium[29].
Gaz parfait diatomique et polyatomique
On considère maintenant un gaz dont les molécules sont composées de deux atomes ou plus. On suppose que les différents atomes sont liés rigidement entre eux. Une telle molécule dispose comme dans le cas précédent de trois degré de libertés associés à son déplacement dans le conteneur. Mais elle peut aussi tourner sur elle-même et accumuler ainsi de l’énergie. Ces degrés de libertés supplémentaires contribuent aux aussi à l’énergie totale et à la chaleur spécifique.
Dans le cas le plus général, si les moments d’inertie principaux de la molécule sont I1, I2 et I3, alors cette énergie cinétique de rotation est donnée par
où ω1, ω2 et ω3 sont les composantes principales de la vitesse angulaire. Ce cas est formellement très similaire au cas précédent ; l’énergie est proportionnelle au carré de la vitesse angulaire. Par un raisonnement identique, l’équipartition implique donc que l’énergie cinétique moyenne de rotation de chaque molécule est 3/2 kBT à l’équilibre.
Il convient de distinguer deux cas, selon que la molécule est linéaire (atomes parfaitement alignés) ou non. Dans le premier cas, la molécule ne peut pas accumuler de l’énergie par rotation autour de son axe : il n’y a que deux degrés de liberté au lieu de trois. La contribution de l’énergie cinétique de rotation à l’énergie totale sera deux fois 1/2 kBT seulement. Pour une molécule non linéaire, l’énergie moyenne totale de rotation est en revanche 3/2 kBT.
Dans les gaz diatomiques tels que l’azote, l’oxygène, les molécules sont composées de deux atomes identiques et sont forcément linéaires. Avec le modèle de molécule que l’on vient de décrire, la chaleur spécifique totale d’un tel gaz diatomique est donc 5/2 R.
Vibration des molécules
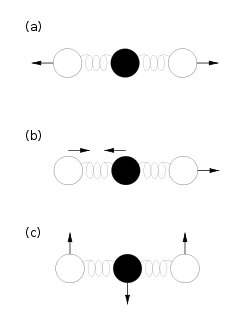 Modes de vibration d’une molécule de CO2. Chaque mode contribue comme un oscillateur harmonique pour kBT à l’énergie totale du gaz. Le 4e mode, identique au (c) à une rotation près, n’est pas représenté ici.
Modes de vibration d’une molécule de CO2. Chaque mode contribue comme un oscillateur harmonique pour kBT à l’énergie totale du gaz. Le 4e mode, identique au (c) à une rotation près, n’est pas représenté ici.
Si on considère qu’une molécule de gaz est un ensemble de plusieurs atomes liés élastiquement et non plus rigidement, alors cette molécule peut vibrer et accumuler de l’énergie dans son mouvement de vibration. On peut alors modéliser un mode de vibration de la molécule par un oscillateur harmonique. Dans le cas le plus simple à une dimension, cet oscillateur a a deux types d’énergie :
- de l’énergie cinétique, fonction de sa masse m et sa vitesse v
- de l’énergie potentielle associée à la force de rappel qui tend à le ramener vers sa position d’équilibre. Cette énergie est fonction de la raideur du ressort a et de l’écart à la position d’équilibre x.
L’énergie totale est alors obtenue en additionnant ces deux énergies :
Le théorème d’équipartition s’applique de la même manière aux deux composantes de l’énergie, chacune comptant pour un degré de liberté. À l’équilibre, l’oscillateur aura donc une énergie moyenne
Chaque oscillateur, donc chaque mode de vibration, a donc une énergie moyenne totale kBT et contribue pour kB à la chaleur spécifique du système. Pour connaître la contribution des vibrations moléculaires à l’énergie totale, il suffit donc de connaître le nombre de ses modes propres de vibrations : une molécule composée de n atomes en possède 3n − 5 si tous les atomes sont alignés comme dans le CO2 représenté ci-contre, et 3n − 6 dans le cas contraire, par exemple pour la molécule d’eau[30].
On verra dans la suite qu’il faut toutefois être prudent : tous les modes ne contribuent pas nécessairement à l’énergie totale selon la température ; la mécanique quantique permettra d’expliquer pourquoi.
Équipartition en théorie cinétique des gaz
Article détaillé : Théorie cinétique des gaz.Les présentations modernes du théorème d’équipartition dans le cadre de la physique statistique sont très générales mais abstraites. Elles ne reflètent que peu les raisonnements d’origine qui s’appliquaient au problème beaucoup plus concret de la théorie cinétique des gaz. Les arguments et démonstrations d’alors, bien que moins généraux, sont utilisés par de nombreux enseignants et auteurs pour leur intérêt pédagogique. Ils permettent de mettre en valeur d’une façon différente les hypothèses fondamentales de l’équipartition.
Dans le cadre de la théorie cinétique des gaz, on considère un système composé d’un très grand nombre de sphères dures dans un conteneur. Ces sphères sont animées d’un mouvement de translation et entrent en collision les unes avec les autres. On peut supposer ici que les sphères n’interagissent pas entre elles en-dehors des collisions. Tout l’enjeu de la théorie est de relier les caractéristiques microscopiques de ces mouvements (masse des particules, vitesses) aux grandeurs macroscopiques que l’on mesure (pression, température).
Des collisions à l’équipartition
 Illustration d’un choc élastique entre deux sphères dures en deux dimensions. Les vitesses des deux sphères après le choc sont déterminées par la conservation de l’énergie totale et de la quantité de mouvement.
Illustration d’un choc élastique entre deux sphères dures en deux dimensions. Les vitesses des deux sphères après le choc sont déterminées par la conservation de l’énergie totale et de la quantité de mouvement.
Lorsque deux particules entrent en collision, elles arrivent toutes deux avec des vitesses différentes, donc des énergies cinétiques différentes, et repartent après le choc avec des directions et des vitesses déterminées par la conservation de la quantité de mouvement et de l’énergie totale. En général, l’énergie d’une particule après le choc est différente de son énergie avant le choc. La collision est donc un moyen d’échanger de l’énergie entre les particules. Dans le modèle le plus simple tel qu’il est proposé ici, c’est même le seul moyen. Pour démontrer l’équipartition de l’énergie dans le cadre de ce modèle, il faut donc montrer comment les collisions tendent à répartir l’énergie équitablement en moyenne entre toutes les particules.
Dans tout ce qui suit, on va considérer des chocs élastiques entre deux sphères dures de masses différentes m1 et m2. On considère le choc par commodité dans le référentiel du centre de masse des deux particules, lui-même animé d’un mouvement de translation rectiligne uniforme par rapport au conteneur (tant qu’aucune particule ne rebondit sur une paroi), avec une vitesse qu’on notera vcm. On notera v1 et v2 les vitesses des particules.
À partir d’un cas particulier, James Maxwell avait avancé que le choc ne pouvait que réduire la différence d’énergie entre les deux particules. À la suite d’un très grand nombre de chocs, l’énergie ne pouvait donc que tendre vers une égalité en moyenne. Cet argument ne suffit pas à montrer que les chocs conduisent à l’équipartition ; il ne s’agit après tout que d’un cas particulier. Toutefois, de manière plus précise, il est possible de montrer que le choc ne peut que réduire la corrélation entre la différence des vitesses des deux particules et la vitesse de leur centre de masse[31]. À l’équilibre, on peut donc supposer que cette corrélation tend vers 0 :
En utilisant l’expression de la vitesse du centre de masse, on en conclut que
Le premier terme de cette somme est proportionnel à la différence d’énergie cinétique moyenne entre les deux particules. Le second terme est la corrélation entre les vitesses initiales des particules. Si on suppose que ces deux vitesses sont indépendantes, autrement dit qu’il n’y a aucune relation a priori entre les vitesses de deux particules avant le choc, alors ce second terme s’annule. C’est ce qu’on appelle l’hypothèse du chaos moléculaire. Dans ce cas, on retrouve donc l’égalité des énergies cinétiques moyennes à l’équilibre :
Notons qu’il n’est pas possible de déduire l’équipartition à partir des équations du choc élastique seulement : ces équations restent réversibles à l’échelle macroscopique, alors que l’évolution vers l’équilibre thermodynamique est un processus irréversible.
Distribution des vitesses à l’équilibre thermodynamique
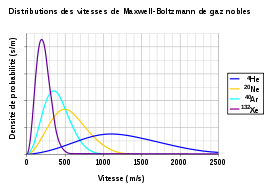
Une fois que l’équilibre thermodynamique est atteint, les vitesses des particules suivent la distribution des vitesses de Maxwell-Boltzmann[32]. Cette distribution est tracée sur la figure ci-contre pour quatre gaz rares. Elle est la seule solution stationnaire de l’équation de Boltzmann. En d’autres termes, les chocs entre particules ne font que modifier les vitesses de particules prises au hasard, mais ne modifient pas la répartition d’ensemble.
On peut vérifier que la distribution de Maxwell-Boltzmann permet de retrouver le théorème d’équipartition pour le gaz parfait monoatomique. Partant de l’expression explicite de la densité de probabilité
pour la vitesse d’une particule de masse m dans le système, on peut calculer l’énergie cinétique moyenne d’une particule par la formule intégrale :
On retrouve ici le fait que chaque particule a exactement la même énergie cinétique moyenne, 3/2 kBT[33].
Théorème d’équipartition en physique statistique
La formulation du théorème d’équipartition s’appuie sur le formalisme de la mécanique hamiltonienne. L’état d’un système physique est caractérisé par ses coordonnées dans l’espace des phases, communément séparées en coordonnées généralisées qk et impulsions généralisées pk, où pk est le moment conjugué à qk. Les (qk,pk) décrivent complètement l’état du système. Un degré de liberté noté xn désignera une de ces coordonnées, autrement dit un qk ou un pk.
Les crochets
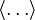 désignent une moyenne d’ensemble sur l’espace des phases. Dans un système ergodique, elle est égale à la moyenne prise sur une durée suffisamment longue, qui est celle que l’on mesure en pratique.
désignent une moyenne d’ensemble sur l’espace des phases. Dans un système ergodique, elle est égale à la moyenne prise sur une durée suffisamment longue, qui est celle que l’on mesure en pratique.Théorème d’équipartition
Énoncé
Le théorème d’équipartition affirme : à l’équilibre thermodynamique, l’énergie moyenne d’un système dont le hamiltonien H s’écrit comme la somme de fonctions quadratiques de ses coordonnées est répartie également entre toutes ses composantes et vaut 1/2 fkBT où f est le nombre de termes de la somme. On peut l’écrire
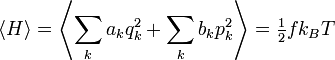
Ce nombre f est souvent désigné comme le nombre de « degrés de liberté » du système, mais c’est un raccourci qui peut être trompeur. Ce nombre compte en réalité le nombre de termes quadratiques du hamiltonien ; il ne correspond pas à la définition habituelle d’un degré de liberté en physique.
Démonstration
Dans l’ensemble canonique, cette formule peut être démontrée par calcul direct de la valeur moyenne à partir de la fonction de partition, classiquement notée Z. Le calcul ramène à des intégrales de fonctions gaussiennes qu’on sait calculer explicitement. On utilise ensuite les relations habituelles de l’ensemble canonique. C’est cette démonstration qui était présentée avant que ne soit introduite la version généralisée du théorème.
Détail du calcul direct de l’énergie moyenne dans l’ensemble canonique
On considère un hamiltonien de la formeLa fonction de partition canonique se réduit alors à un produit d’intégrales de fonctions gaussiennes :
Connaissant la valeur de l’intégrale de la fonction gaussienne, on peut écrire :
En notant f le nombre de termes du hamiltonien, on a donc
Dans l’ensemble canonique, l’énergie moyenne du système est donnée par
On retrouve alors le théorème :
Théorème généralisé
Énoncé
On appelle théorème d’équipartition généralisé une formule démontrée pour la première fois par Tolman en 1918[34] qui étend l’idée de l’équipartition pour des hamiltoniens de forme générale. Même si la présentation qui en est faite diffère légèrement d’un auteur à l’autre, c’est en général cette formule qui est démontrée dans les ouvrages généraux de physique statistique. Ce théorème généralisé affirme que pour un système à l’équilibre thermodynamique à la température T, décrit par un hamiltonien H et des degrés de liberté xn, on a, pour tous les indices n et m,
δnm est le symbole de Kronecker qui vaut 1 si n = m et 0 dans les autres cas.
Dans ce cas général, aucune hypothèse n’est faite sur la forme du hamiltonien. En contrepartie, l’énergie n’est pas nécessairement répartie de manière égale entre toutes ces composantes : il n’y a pas nécessairement « équipartition » de l’énergie au sens strict. On en verra un exemple dans le cas de la sédimentation de particules. C’est pourquoi plusieurs auteurs ne reprennent pas l’appellation « théorème d’équipartition généralisé » proposée initialement par Tolman.
Bien entendu, cette formule générale permet de retrouver le résultat particulier du paragraphe précédent.
Démonstrations
Le résultat général peut se démontrer dans l’ensemble microcanonique quand l’énergie totale du système est constante, et aussi dans l’ensemble canonique, quand le système est couplé à une source de chaleur avec laquelle il peut échanger de l’énergie. Dans un cas comme dans l’autre, la démonstration procède par le calcul explicite de la moyenne sur l’espace des phases.
Dans tous les cas, on notera dΓ l’élément de volume infinitésimal de l’espace des phases
dΓ = ∏ dqidpi i .
Dans l’ensemble microcanonique, le système est isolé du reste du monde, ou au moins très faiblement couplé. De la sorte, son énergie totale est constante. On dit que l’énergie totale H est confinée entre E et ΔE. Pour une énergie E donnée et un écart ΔE, on note Γ(E,ΔE) le volume de la région de l’espace des phases dans laquelle l’énergie du système est comprise entre E et E + ΔE :
![\Gamma (E, \Delta E) = \int_{H \in \left[E, E+\Delta E \right]} \mathrm d\Gamma](/pictures/frwiki/48/019ff4a3cf9a30224c81d6dc024122a0.png) .
.
La probabilité d’occupation de tous les états de cette région est la même, par définition de l’ensemble microcanonique. La valeur moyenne d’une grandeur X s’écrit alors
On peut alors montrer que
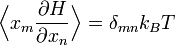 .
.
Détail du calcul dans l’ensemble microcanonique
On note maintenant ΣE le volume total de l’espace des phases dans lequel l’énergie est inférieure à E :Σ(E) = ∫ dΓ H < E .
Puisque ΔE est très petit devant E, les intégrations suivantes sont équivalentes
de sorte que Γ est proportionnel à ΔE
où ρ(E) est la densité d’états. On introduit enfin la définition usuelle de l’entropie en physique statistique :
et celle de la température microcanonique T :
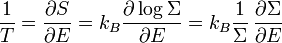 .
.
Avec ces définitions, la moyenne sur les variables xm et xn (qui peuvent être des pk ou des qk) est donnée par
En utilisant les résultats précédents, on peut faire apparaître la densité d’état ρ :
où la dernière égalité provient de ce que E est constante et ne dépend pas de xn. Une intégration par parties donne alors
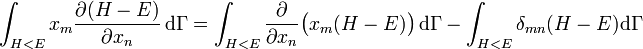 .
.
La première intégrale est nulle (elle peut être réécrite comme une intégrale de H − E sur l’hypersurface où H = E). Il reste donc
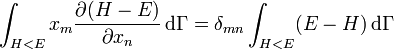 .
.
La substitution de ce résultat dans l’équation précédente donne
Puisque
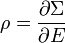 le théorème d’équipartition s’en suit :
le théorème d’équipartition s’en suit :On retrouve la formulation générale du théorème.
Dans l’ensemble canonique, on considère le système en équilibre thermodynamique avec une source de chaleur de température fixe T (en Kelvin). La probabilité d’occupation de chaque état dans l’espace des phases est donnée par son facteur de Boltzmann multiplié par un facteur de normalisation qui assure que la somme des probabilités est bien égale à un et dont la valeur n’importe pas ici ; on le notera
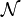 . La valeur moyenne d’une quantité X est alors définie par
. La valeur moyenne d’une quantité X est alors définie parLe calcul explicite (qui fait essentiellement appel à une intégration par partie) donne le résultat souhaité.
Détail du calcul dans l’ensemble canonique
On cherche à calculerUne intégration par parties sur la variable xk nous donne
où dΓk = dΓ / dxk indique que la première intégration n’est pas faite sur xk.
Le premier terme est nul ; on peut s’en convaincre en considérant le cas d’un gaz dans un conteneur. Si xk est une impulsion généralisée, alors l’énergie cinétique associée devient infinie aux bornes. Si xk est une coordonnée, ses valeurs maximale et minimale sont atteintes aux parois du conteneur pour lesquelles l’énergie potentielle tend vers l’infini. Dans les deux cas, l’exponentielle tend vers 0. De plus, on reconnaît la fonction de partition dans la seconde intégrale qui vaut donc 1. La formule recherchée s’en suit donc immédiatement :
Théorème d’équipartition et théorème du viriel
Article détaillé : Théorème du viriel.Le théorème d’équipartition est étroitement lié au théorème du viriel qui s’applique lui aussi aux systèmes à plusieurs particules. Ce dernier a d’ailleurs été proposé par Rudolf Clausius[35] lors des développements des fondements de la thermodynamique, alors qu’il cherchait à relier les notions de température et de chaleur aux mouvements des molécules de gaz.
Partant du théorème d’équipartition généralisé, en utilisant les relations de la mécanique hamiltonienne, on peut écrire :
D’après le principe fondamental de la dynamique, la dérivée de pk par rapport au temps est égale à la force généralisée Fk agissant sur la particule. On peut donc écrire
Toujours d’après le théorème d’équipartition, on sait que la valeur moyenne de l’énergie cinétique pour un degré de liberté vaut kBT / 2. En combinant ces deux relations, on obtient donc :
Cette relation est très semblable au théorème du viriel tel qu’énoncé à l’origine par Clausius : pour un ensemble de particules de masse m animées d’un mouvement stable, repérées par leurs positions
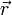 et leurs vitesses
et leurs vitesses 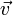 , sur lesquelles s’exerce des forces
, sur lesquelles s’exerce des forces 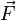 , on a
, on aLa différence majeure réside dans le fait qu’il s’agit dans ce dernier cas d’une moyenne temporelle, représentée par le trait horizontal, et non plus d’une moyenne d’ensemble. De manière générale, le théorème de Birkhoff montre que l’égalité de ces deux moyennes est vérifiée pour les systèmes ergodiques.
Applications classiques de l’équipartition
Loi de Dulong et Petit
Article détaillé : Loi de Dulong et Petit.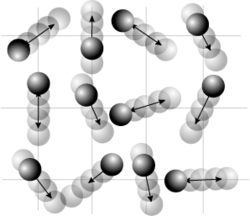 Dans un cristal, les atomes oscillent autour de leur position d’équilibre. La contribution de ces oscillations à la chaleur spécifique conduit à la loi de Dulong et Petit.
Dans un cristal, les atomes oscillent autour de leur position d’équilibre. La contribution de ces oscillations à la chaleur spécifique conduit à la loi de Dulong et Petit.
La loi de Dulong et Petit sur la chaleur spécifique des solides se déduit très simplement de ce qui précède[36]. On considère un cristal composé de N atomes. Chacun de ces atomes occupe une position d’équilibre autour de laquelle il peut osciller. Ce mouvement peut se faire dans les trois directions de l’espace, de manière indépendante. Le solide peut donc être considéré en première approche comme un système de 3N oscillateurs harmoniques indépendants.
On a vu précédemment qu’un oscillateur harmonique a une énergie moyenne kBT. L’énergie moyenne totale du solide est 3NkBT, sa chaleur spécifique est 3NkB. La chaleur spécifique molaire de ce matériau est donc 3NAkB où NA est le nombre d’Avogadro, ce qui s’écrit encore 3R où R est la constante des gaz parfaits. On retrouve bien la loi de Dulong et Petit selon laquelle la chaleur spécifique molaire des solides est indépendante de la nature du solide et égale à 3R, soit environ 6 cal/(mol·K).
Dérivation de la loi des gaz parfaits
Le théorème d’équipartition peut être utilisé pour retrouver la loi des gaz parfaits à partir de la mécanique classique. Ce calcul consiste à calculer le viriel du gaz de deux façons différentes.
On note
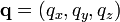 et
et 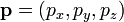 les vecteurs positions et quantité de mouvement d’une particule dans le gaz et
les vecteurs positions et quantité de mouvement d’une particule dans le gaz et 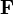 la force totale s’exerçant sur cette particule, alors
la force totale s’exerçant sur cette particule, alorsoù la première égalité est donnée par la seconde loi de Newton, et la seconde ligne utilise les équations de Hamilton et le théorème d’équipartition. La sommation sur l’ensemble des N particules du système donne
En vertu de la troisième loi de Newton et de l’hypothèse du gaz parfait, la force totale sur le système est la force appliquée par les parois du conteneur, et cette force est donnée par la pression P du gaz. En conséquence :
où
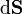 est un élément de surface infinitésimal sur la paroi du conteneur. En utilisant le théorème de Green-Ostrogradsky, on peut calculer
est un élément de surface infinitésimal sur la paroi du conteneur. En utilisant le théorème de Green-Ostrogradsky, on peut calculeroù dV est un élément de volume infinitésimal dans le conteneur et V est son volume total. En regroupant des égalités, on obtient
ce qui nous donne immédiatement la loi des gaz parfaits pour N particules :
où n = N / Na est le nombre de moles de gaz et R = NAkB est la constante des gaz parfaits.
Étude d’un mouvement brownien
 Mouvement brownien typique d’une particule en deux dimensions. Le théorème d’équipartition permet de retrouver en moyenne les caractéristiques de ce mouvement aléatoire au cours du temps.
Mouvement brownien typique d’une particule en deux dimensions. Le théorème d’équipartition permet de retrouver en moyenne les caractéristiques de ce mouvement aléatoire au cours du temps.
Le mouvement brownien désigne une description mathématique du mouvement aléatoire d’une grosse particule immergée dans un fluide et qui n’est soumise à aucune autre interaction que des chocs avec les petites molécules du fluide environnant. Les mécanismes en œuvre dans ce type de mouvement sont proches des idées de la théorie cinétique des gaz. Le théorème d’équipartition fut utilisé très tôt, dès 1879, pour caractériser un tel mouvement[37].
On peut partir de l’équation de Langevin selon laquelle le mouvement d’une particule de masse m et de vitesse v est régi par la seconde loi de Newton qui s’écrit
où
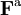 est une force aléatoire représentant les collisions aléatoires entre la particule et les molécules voisines, et où la constante de temps τ reflète la force de frottement fluide qui s’oppose au mouvement de la particule dans la solution. La trainée est souvent notée
est une force aléatoire représentant les collisions aléatoires entre la particule et les molécules voisines, et où la constante de temps τ reflète la force de frottement fluide qui s’oppose au mouvement de la particule dans la solution. La trainée est souvent notée 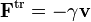 , la constante de temps est alors m / γ.
, la constante de temps est alors m / γ.En faisant le produit scalaire de cette équation avec le vecteur position
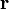 , puis une moyenne, on obtient
, puis une moyenne, on obtientpour le mouvement brownien (puisque la force aléatoire
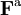 et la position
et la position 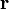 ne sont pas corrélées). En utilisant les identités remarquables
ne sont pas corrélées). En utilisant les identités remarquableset
l’équation de base du mouvement brownien peut être transformée en
où la dernière égalité provient du théorème d’équipartition pour l’énergie cinétique de translation :
L’équation différentielle ci-dessus pour
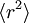 a une solution exacte (pour des conditions initiales convenables) :
a une solution exacte (pour des conditions initiales convenables) :À une échelle de temps très courte, i.e. pour
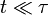 , la particule se comporte comme une particule libre : en utilisant le développement de Taylor de la fonction exponentielle, le carré de la distance croît quadratiquement :
, la particule se comporte comme une particule libre : en utilisant le développement de Taylor de la fonction exponentielle, le carré de la distance croît quadratiquement :En revanche, à une échelle de temps plus longue, pour
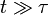 , l’exponentielle et les termes constants deviennent négligeables et le carré de la distance ne croît que linéairement :
, l’exponentielle et les termes constants deviennent négligeables et le carré de la distance ne croît que linéairement :Ceci décrit la diffusion de la particule dans le temps. Une équation analogue pour la diffusion de la rotation d’une molécule rigide peut être calculée de la même manière.
Étude de la sédimentation de particules
Le théorème d’équipartition généralisé a été appliqué à l’étude de la sédimentation de particules en suspension sous l’influence de la gravité[38]. On considère pour cela des particules pesantes (par exemple de grosses protéines) dans l’eau. Les chocs entre ces particules produisent un mécanisme de diffusion qui tend à homogénéiser la concentration des protéines dans tout le récipient. Par ailleurs, la gravité tend à faire tomber toutes les protéines vers le bas du récipient. Une fois que l’équilibre entre ces deux mécanismes antagonistes a été atteint, il est possible de déterminer grâce au théorème d’équipartition l’énergie potentielle moyenne d’une particule et donc sa position moyenne. Pour une bouteille infiniment haute, l’énergie potentielle de gravitation d’une particule de masse mb est donnée par
où z est la hauteur d’une particule dans la bouteille et g est l’accélération de la pesanteur.
Ce processus peut trouver une application dans l’étude de la sédimentation de protéines qui diffusent la lumière et donnent un aspect trouble qu’on peut parfois voir dans la bière[39]. Puisque s = 1, l’énergie potentielle moyenne d’un groupe de protéine est kBT. Donc, si les groupes de protéines ont une masse de 107 uma (à peu près la taille d’un virus), l’aspect sera trouble jusqu’à une hauteur moyenne de 2 cm à l’équilibre.
Ce processus de sédimentation est plus précisément décrit par l’équation de Mason-Weaver[40].
Calcul du bruit thermique dans les composants électroniques
Article détaillé : Bruit thermique.Le théorème d’équipartition peut être utilisé pour démontrer l’expression du bruit thermique dans les composants électroniques[41]. Dans une résistance, l’agitation thermique des électrons de conductions crée des fluctuations de densité électronique, donc de courant électrique, qui conduisent à la présence d’un bruit blanc même en l’absence de toute tension appliquée. Aux bornes d’une résistance, ce bruit est donné par la relation :
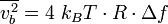
où
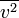 est la variance de la tension aux bornes de la résistance, R est la résistance exprimée en ohms, et
est la variance de la tension aux bornes de la résistance, R est la résistance exprimée en ohms, et 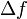 , la bande passante considérée.
, la bande passante considérée.Cette formule permet de prévoir le bruit minimum présent sur un système électronique, et donc sa limite de détection. Le même phénomène de bruit thermique est observé aux bornes d’une capacité. C’est une limitation des capteurs photographiques.
Problème de l’oscillateur anharmonique
Un oscillateur anharmonique est un oscillateur pour lequel l’énergie potentielle n’est pas une fonction quadratique de l’élongation q (la position généralisée qui mesure l’écart de l’oscillateur à la position d’équilibre). Ces oscillateurs donnent un point de vue complémentaire sur le théorème d’équipartition[42]. On peut prendre des exemples simples avec des énergies dont l’expression est de la forme
- Hpot = Cqs
où C et s sont des nombres réels arbitraires. Dans ce cas, le théorème d’équipartition prédit que
Ainsi, l’énergie potentielle moyenne est égale à kBT / s et non plus kBT / 2 comme pour l’oscillateur harmonique (pour lequel s = 2).
Plus généralement, l’expression de l’énergie d’un système à une dimension a un développement de Taylor en fonction de l’élongation q
Il n’y a pas de terme pour n = 1 car à l’équilibre, la force totale s’exercant sur le système est nulle et donc la dérivée première de l’énergie est nulle. Le terme constant pour n = 0 est inutile, puisque l’énergie à l’équilibre peut être posée égale à 0 par convention. Dans ce cas, le théorème d’équipartition affirme que[42]
Contrairement aux autres exemples cités ici, la formule de l’équipartition
ne permet pas d’écrire l’énergie potentielle moyenne en fonction de constantes connues.
Échecs de l’équipartition
L’équipartition de l’énergie, malgré sa grande généralité, est un résultat valable sous certaines hypothèses (ergodicité, équilibre thermodynamique) et dans certaines limites (effets quantiques négligeables). Les paragraphes qui suivent détaillent différents cas pour lesquels l’équipartition ne s’applique pas.
Dans les systèmes non ergodiques
Article connexe : hypothèse d'ergodicité.Le théorème d’équipartition est valable seulement pour les systèmes ergodiques à l’équilibre thermodynamique, pour lesquels tous les états de même énergie ont la même probabilité d’être occupé. Dans un système ergodique, il doit être possible d’échanger de l’énergie entre ses différentes formes dans le système, afin qu’elle puisse se répartir en parts égales au cours du temps. Dans le cas d’un gaz parfait, ce sont les chocs entre molécules qui assurent ces échanges d’énergie.
Paradoxalement, il existe peu de systèmes dont l’ergodicité a pu être prouvée rigoureusement. Un exemple célèbre est le billard de Yakov Sinai[43]. Les conditions qui permettent d’assurer l’ergodicité d’un système isolé - et donc l’équipartition - ont été étudiées et ont donné naissance à la théorie ergodique.
Un contre-exemple fréquemment cité où l’énergie n’est pas partagée entre ses différentes formes, et donc où l’équipartition ne s’applique pas dans l’ensemble microcanonique est un système d’oscillateurs harmoniques couplés[44]. Si le système est isolé, l’énergie de chaque mode normal est constante et fixée à sa valeur initiale.
Si on perturbe un tel système en introduisant des termes de couplage non linéaires suffisamment forts, l’énergie peut être transférée d’un mode à l’autre, on peut alors sous certaines conditions retrouver l’ergodicité et revenir dans le champ d’application du théorème d’équipartition. Mais il ne suffit pas d’une petite perturbation pour rendre un système ergodique : c’est ce que montre le théorème de Kolmogorov–Arnold–Moser. Même un système chaotique, donc extrêmement sensible aux conditions intiales, n’est pas nécessairement ergodique, même si c’est habituellement une hypothèse raisonnable[44].
Pour des niveaux d’énergie quantifiés
Les démonstrations données précédemment supposent que l’énergie est une fonction continue sur l’espace des phases. Or, dans un système quantique, les niveaux d’énergie sont au contraire discrets. Pour que le théorème s’applique, il est donc nécessaire que les niveaux d’énergie soient suffisamment rapprochés pour qu’on puisse la considérer tout de même comme continue. On parle alors d’approximation classique. Ceci n’est réalisé qu’à la condition que l’énergie thermique kBT soit beaucoup plus grande que l’écart entre deux niveaux d’énergie. Dans le cas contraire, les calculs ne sont plus valides, le degré de liberté considéré est dit « gelé », l’équipartition ne s’applique plus.
Oscillateur harmonique quantique
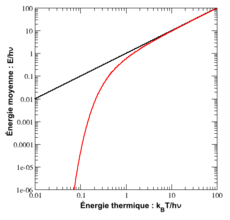
Le cas de l’oscillateur harmonique est un exemple particulièrement important. On a vu précédemment que selon le théorème d’équipartition, son énergie moyenne est égale à kBT. Dans le cas quantique, on peut calculer explicitement son énergie moyenne. Ses niveaux d’énergie sont donnés par En = nhν[45] où h est la constante de Planck, ν est la fréquence de l’oscillateur et n est un entier positif. Dans l’ensemble canonique, la probabilité qu’un niveau d’énergie soit occupé est donné par son facteur de Boltzmann
β = 1 / (kBT) est la température statistique et Z est la fonction de partition donnée par
L’énergie moyenne de l’oscillateur est donnée par
ou encore, en utilisant la relation classique de l’ensemble canonique
On peut donc calculer explicitement l’énergie moyenne :
Cette énergie moyenne est tracée sur la figure ci-contre et comparée au cas classique. Pour les hautes températures, quand l’énergie thermique kBT est très supérieure à l’écart hν entre deux niveaux, l’argument de l’exponentielle tend vers 0 et l’énergie moyenne tend vers kBT, conformément au théorème d’équipartition. En revanche, pour les basses températures, quand
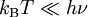 , l’énergie moyenne tend vers 0, le degré de liberté est dit « gelé ». On peut ainsi définir une température caractéristique de l’oscillateur Tosc = hν / kB en dessous de laquelle les effets quantiques se font sentir.
, l’énergie moyenne tend vers 0, le degré de liberté est dit « gelé ». On peut ainsi définir une température caractéristique de l’oscillateur Tosc = hν / kB en dessous de laquelle les effets quantiques se font sentir.Retour sur le gaz diatomique
 Simulation du tracé de la chaleur spécifique d’un gaz diatomique en fonction de la température. Le théorème d’équipartition est vérifié à hautes températures, en général des températures bien plus élevées que la température ambiante. La baisse de la chaleur spécifique aux températures plus basses est due à des effets quantiques.
Simulation du tracé de la chaleur spécifique d’un gaz diatomique en fonction de la température. Le théorème d’équipartition est vérifié à hautes températures, en général des températures bien plus élevées que la température ambiante. La baisse de la chaleur spécifique aux températures plus basses est due à des effets quantiques.
Les gaz diatomiques donnent un bon exemple de cette limitation. On peut modéliser une molécule d’un tel gaz par deux masses reliées par un ressort. Une telle molécule possède trois degrés de liberté en translation, deux degrés de liberté en rotation, et constitue de plus un oscillateur harmonique. Le théorème d’équipartition prédit donc que la chaleur spécifique du gaz est égale à 7/2 R. C’est effectivement le cas dans la limite des hautes températures.
Si on considère maintenant que la molécule est un oscillateur harmonique quantique, on peut, comme précédemment, associer une température caractéristique Tvib à son mouvement de vibration. Si on descend à des températures plus basses que Tvib, le mouvement de vibration de la molécule est gelé, presque toutes les molécules du gaz sont dans leur état fondamental. Le théorème ne s’applique plus. On peut cependant le retrouver en considérant la molécule, non plus comme deux masses reliées par un ressort, mais comme deux masses reliées par un lien rigide. C’est le modèle du rotateur rigide pour lequel la chaleur spécifique n’est plus que de 5/2 R.
Dans la pratique, la plupart des gaz diatomiques ont des températures Tvib très élevées, de sorte qu’à température ambiante, leur chaleur spécifique est effectivement très proche de 5/2 R. Un exemple typique est le monoxyde de carbone, CO, pour lequel Tvib vaut 3103 K. Pour les molécules avec des atomes lourds ou faiblement liés, Tvib peut approcher la température ambiante ; par exemple, elle vaut 308 K (35°C) pour le diiode gazeux I2[46].
Ce qui vient d’être dit pour le mouvement de vibration de la molécule s’applique aussi bien à son mouvement de rotation. Mais les températures caractéristiques sont bien plus basses. Pour le monoxyde de carbone, Trot vaut environ 1,8 K. Le gel du mouvement de rotation ne s’observe donc qu’à des températures très basses.
De manière générale, ces effets interviennent chaque fois que la séparation entre deux niveaux d’énergie est beaucoup plus grande que l’agitation thermique. Un autre exemple est donné par les énergies des états excités des électrons dans un atome d’hydrogène. Ceux-ci ne contribuent pas à la chaleur spécifique de l’hydrogène gazeux à température ambiante, car l’énergie thermique kBT (environ 0,025 eV) est beaucoup plus faible que l’écart entre l’état fondamental et le premier état excité (environ 10 eV).
Dans les gaz dégénérés
Dans le paragraphe qui précède, on a pris en compte des effets quantiques, mais partiellement seulement : on a traité les particules comme des objets classiques indépendants dont seuls les niveaux d’énergie (de rotation ou de vibration) sont quantifiés, tout en restant dans le cadre de la statistique de Maxwell-Boltzmann. Cette approche n’est pas valable quand les fonctions d’onde des particules commencent à se superposer : il faut alors tenir compte de leur nature quantique et les traiter dans le cadre des statistiques quantiques : statistique de Fermi-Dirac pour les fermions, statistique de Bose-Einstein pour les bosons. On parle de matière dégénérée.
Ces effets dominent dans les limites des fortes densités et des basses températures. Ils sont importants dans la structure des naines blanches et des étoiles à neutrons. Un cas plus quotidien se présente dans les métaux : les électrons de valence d’un métal peuvent avoir une énergie cinétique moyenne de quelques eV. Cette énergie correspondrait à des températures de plusieurs dizaines de milliers de degrés selon le théorème de l’équipartition.
Un critère de validité de l’équipartition fut initialement calculé par Einstein[47] dans sa théorie du gaz parfait quantique. Dans ce travail, il montre que l’équipartition peut être considérée comme valide dans la limite où
Dans le cas de l’hydrogène, le calcul explicite du terme de gauche donne environ 60000, ce qui justifie a posteriori la validité de l’équipartition. Quand on s’approche du cas quantique, la correction à l’équipartition au premier ordre s’écrit
Ce critère de validité est plus souvent cité en faisant apparaître la longueur d’onde de de Broglie λDB associée :
On peut alors interpréter ce critère : l’équipartition reste valable tant que cette longueur d’onde reste très inférieure à la distance moyenne entre les particules.
Dans les gaz relativistes
On n’a utilisé jusque là que des équations de la mécanique newtonienne. Toutefois, les effets relativistes peuvent dominer dans certains systèmes lorsque les particules de gaz acquièrent des vitesses comparables à la vitesse de la lumière c ; on parle alors de gaz parfait relativiste. Dans le cas le plus général, l'équipartition n'est alors pas vérifiée[48], mais on peut la retrouver dans les deux cas limite du gaz parfait classique et du gaz ultra-relativiste.
Dans le gaz parfait classique (monoatomique), on considérait que l'énergie du système n'était constituée que d'énergie cinétique de translation. Dans le cadre de la mécanique relativiste, l'énergie totale est égale à la somme de l'énergie cinétique et d'une énergie qui dépend de la masse au repos de la particule. La prise en compte de cette énergie rompt l'équipartition : si les particules du gaz ont des masses différentes, l'énergie ne peut pas être répartie équitablement. Dans le cas le plus général, l'énergie totale s'écrit
Ni l'énergie totale, ni l'énergie cinétique ne sont réparties équitablement entre les différents degrés de liberté. Il est possible néanmoins de définir une grandeur homogène à une énergie qui obéit à une relation similaire à l'équipartition[49].
Dans la limite où les particules ont des vitesses très faibles devant la vitesse de la lumière, on retrouve le résultat classique. L'énergie totale d'une particule s'écrit
L'équipartition est bien respectée pour l'énergie cinétique, mais pas pour l'énergie totale, qui prend en compte le terme supplémentaire dépendant de la masse.
Dans la limite dite ultra-relativiste pour laquelle les particules ont des vitesses très proches de celle de lumière, on retrouve l'équipartition pour l’énergie totale qui s'écrit :
Le calcul montre que l’énergie moyenne totale d’un gaz ultra-relativiste vaut deux fois celle d’un gaz non relativiste[50] : pour N particules, elle vaut 3 NkBT.
Dans les simulations numériques
On étudie souvent les systèmes en physique statistique aux moyens de techniques de simulation numérique, dont la dynamique moléculaire. Les conditions aux limites périodiques parfois utilisées dans ces études imposent des contraintes supplémentaires au système (conservation du moment linéaire total et de la position du centre de masse par exemple) qui induisent des effets non négligeables dans la limite des petits systèmes contenant des particules de masses hétérogènes. Dans ces conditions, l’équipartition de l’énergie n’est plus valable[51]. D’autres effets sont par exemple des écarts à la distribution de Maxwell-Boltzmann, ou la non équivalence des approches canonique et microcanonique. Il est toutefois possible de démontrer des formules généralisant le théorème d’équipartition à ces cas plus exotiques[52].
Notes et références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Equipartition theorem ».
- ↑ (en) Waterston JJ, Thoughts on the Mental Functions, 1843 (réimprimé dans ses Papers, 3, 167, 183.)
- ↑ Cette publication de 1873 contient à la fois le mémoire, la préface de Rayleigh ainsi que des reproductions des deux résumés de 1846 et 1851. Voir Waterston JJ, « On the physics of media that are composed of free and elastic molecules in a state of motion », dans Philos. Trans. R. Soc. London, vol. 183, 1893, p. 1–79 [texte intégral]
- ↑ Texte original : « Equilibrium of pressure and heat between two gases takes place when the number of atoms in unity of volume is equal, and vis viva of each atom equal. Temperature, therefore, in all gases, is proportional to the mass of one atom multiplied by the mean square of the molecular motions, being measured from an absolute zero 491° below the zero of Fahrenheit’s thermometer. »
- ↑ Maxwell JC, The Scientific Papers of James Clerk Maxwell (Volume 2), Dover, New York, 2003 (ISBN 978-0486495606), « On Boltzmann’s theorem on the average distribution of energy in a system of material points », p. 716.
- ↑ Texte original : « Hence at a given temperature the total kinetic energy of a material system must be the product of the number of degrees of freedom of that system into a constant which is the same for all substances at that temperature, being in fact the temperature of the thermodynamic scale multiplied by an absolute constant. »
- ↑ Bergia et Navarro 1997, p. 185-186
- ↑ A. T. Petit et P. L. Dulong, « Recherches sur quelques points importants de la théorie de la chaleur », dans Annales de Chimie et de Physique, vol. 10, 1819, p. 395–413 [texte intégral]
- ↑ (de) Kundt A, Warburg E, « Über die spezifische Wärme des Quecksilbergases (De la chaleur spécifique des gaz de mercure) », dans Annalen der Physik, vol. 157, 1876, p. 353–369 [texte intégral]
- ↑ de la Rive A, Marcet F, « Quelques recherches sur la chaleur spécifique », dans Annales de Chimie et de Physique, vol. 75, 1840, p. 113–144 [texte intégral]
- ↑ Henri Victor Regnault, « Recherches sur la chaleur spécifique des corps simples et des corps composés (deuxième Mémoire) », dans Annales de Chimie et de Physique, vol. 1 (3e Série), 1841, p. 129–207 [texte intégral] Présenté à l’Académie des Sciences le 11 janvier 1841.
- ↑ (en) James Dewar, « The Specific Heat of Carbon at High Temperatures », dans Philosophical Magazine, vol. 44, 1872, p. 461
- ↑ (de) Heinrich Friedrich Weber, « Die spezifische Wärme des Kohlenstoffs (Chaleur spécifique du carbone) », dans Annalen der Physik, vol. 147, 1872, p. 311–319 [texte intégral]
- ↑ (de) Heinrich Friedrich Weber, « Die spezifische Wärmen der Elemente Kohlenstoff, Bor und Silicium (Chaleur spécifiques des éléments carbone, bore et silicium) », dans Annalen der Physik, vol. 154, 1875, p. 367–423, 553–582 [texte intégral]
- ↑ (de) Wüller A., Lehrbuch der Experimentalphysik (Physique expérimentale), vol. 2, Teubner, Leipzig, 1896, p. 507 et suivantes
- ↑ (de) Eucken A., « Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen (Chaleur spécifique moléculaire de l’hydrogène à basses températures) », dans Sitzungsberichte der königlichen Preussischen Akademie der Wissenschaften, vol. 1912, 1912, p. 141–151
- ↑ a et b (en) Charles Kittel, Introduction to Solid State Physics, 1996 [détail des éditions], p. 151-156
- ↑ a et b (de) Albert Einstein, « Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (D’un modèle heuristique de la création et de la transformation de la lumière) », dans Annalen der Physik, vol. 17, 1905, p. 132-148 [texte intégral]
- ↑ (en) John Rayleigh, « Remarks upon the Law of Complete Radiation », dans Philosophical Magazine, vol. 49, 1900, p. 539–540
- ↑ The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, Series 6, volume 2, page 1 (1901)
- ↑ WD Niven et James Clerk Maxwell, The Scientific Papers of James Clerk Maxwell, vol. 2, At the University Press, Cambridge, 1890, p. 418–438 Conférence tenue par JC Maxwell à la Chemical Society le 18 février 1875
- ↑ Bergia et Navarro 1997, p. 187. Les idées de Kelvin sur ce point sont notamment données dans les cours qu’il donne à Baltimore. Voir William Thomson, Baltimore Lectures, Johns Hopkins University Press, Baltimore, 1904 Réédité par la suite en 1987 par MIT Press sous le titre Kelvin’s Baltimore Lectures and Modern Theoretical Physics: Historical and Philosophical Perspectives (éditeur : Robert Kargon et Peter Achinstein), ISBN 978-0262111171
- ↑ (en) Boltzmann L, « On certain Questions of the Theory of Gases », dans Nature, vol. 51, 1895, p. 413–415
- ↑ Lord Rayleigh, 1900
- ↑ Klein, Paul Ehrenfest. vol 1, The making of a theoretical physicist (3ème édition), Amsterdam, 1985
- ↑ Bergia et Navarro 1997, p. 184
- ↑ (de) Albert Einstein, « Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme », dans Annalen der Physik, vol. 22, 1907, p. 180 [texte intégral]
(de) Einstein A., « Berichtigung zu meiner Arbeit: 'Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme' (Corrections à l’article précédent) », dans Annalen der Physik, vol. 22, 1907, p. 800 - ↑ Bergia et Navarro 1997, p. 219
- ↑ Voir par exemple F Bloch, Fundamentals of Statistical Mechanics, Imperial college Press, London, 2000, p. 94.
- ↑ Cette méthode est toutefois très consommatrice d’énergie ; elle tend à être replacée par des méthodes plus modernes.
- ↑ (en) « Vibration of Polyatomic Molecules » dans Introduction to Quantum Mechanics, Academic Press, 2004 (ISBN 0121060519), p. 220
- ↑ Pour la démonstration, voir Peliti 2007
- ↑ voir par exemple Diu 1996, p. 350 pour une démonstration des résultats principaux de la théorie cinétique des gaz.
- ↑ Diu 1996, p. 353
- ↑ Tolman 1918
- ↑ (de) Rudolf Clausius, « Ueber einen auf die Wärme anwendbaren mechanischen Satz », dans Annalen der Physik, vol. 141, 1870, p. 124–130 [texte intégral]
(en) Rudolf Clausius, « On a Mechanical Theorem Applicable to Heat », dans Philosophical Magazine, Ser. 4, vol. 40, 1870, p. 122–127 - ↑ voir par exemple Diu 1996, p. 381 pour ce résultat dans le cadre d'une présentation plus générale du calcul de la chaleur spécifique des solides.
- ↑ Bergia et Navarro 1997, p. 188
- ↑ Tolman 1918
- ↑ (en) Miedl M, Garcia M, Bamforth C, « Haze formation in model beer systems », dans J. Agric. Food Chem., vol. 53, no 26, 2005, p. 10161-5 [lien PMID]
- ↑ (en) Mason M, Weaver W, « The Settling of Small Particles in a Fluid », dans Physical Review, vol. 23, 1924, p. 412–426
- ↑ Mandl 1971
- ↑ a et b Richard Tolman 1927, p. 76-77
- ↑ Arnold V., Avez A., Théorie ergodique des systèmes dynamiques, Gauthier-Villars, Paris, 1967
- ↑ a et b (en) Reichl LE, A Modern Course in Statistical Physics, Wiley Interscience, 2e édition, 1998 (ISBN 978-0471595205), p. 326–333
- ↑ Les niveaux d’énergie sont rigoureusement En = (n + 1 / 2)hν. Le terme constant hν / 2 est omis ici car il ne joue aucun rôle dans les calculs qui suivent.
- ↑ McQuarrie 2000
- ↑ Bergia et Navarro 1997
- ↑ Pour une présentation des propriétés du gaz parfait relativiste, voir Greiner 1999.
- ↑ (en) A. Komar, « Relativistic equipartition », dans General Relativity and Gravitation, vol. 28, 1996, p. 379-385 [texte intégral]
- ↑ Greiner 1999
- ↑ (en) Shirts RB, Burt SR et Johnson AM, « Periodic boundary condition induced breakdown of the equipartition principle and other kinetic effects of finite sample size in classical hard-sphere molecular dynamics simulation », dans Journal of Chemical Physics, vol. 125, 2006, p. 164102 [texte intégral]
- ↑ (en) Uline JM, Siderius DW et Corti DS, « On the generalized equipartition theorem in molecular dynamics ensembles and the microcanonical thermodynamics of small systems », dans Journal of Chemical Physics, vol. 128, 2008, p. 124301 [texte intégral]
Voir aussi
Bibliographie
Ouvrages de physique statistique
- (fr) Lev Landau et Evguéni Lifchitz, Physique théorique, tome 5 : Physique statistique, éd. MIR, Moscou [détail des éditions]
- (fr) Claudine Guthmann, Danielle Lederer et Bernard Roudet, Éléments de physique statistique, 1996 [détail des éditions]
- Walter Greiner, Ludwig Neise, Horst Stöcker (trad. Hans Aksas), Thermodynamique et physique statistique, Springer, 1999, p. 225-230
- (fr) Cours de physique de Feynman, volume 1, chap. 39, « théorie cinétique des gaz ».
- (en) R. Pathria, Statistical Mechanics, Pergamon Press, 1972 (ISBN 0-08-016747-0), p. 43–48, 73–74
- (en) Kerson Huang, Statistical Mechanics, John Wiley and Sons, 1987 (ISBN 0-471-81518-7), p. 136–138
- (en) F. Mandl, Statistical Physics, John Wiley and Sons, 1971 (ISBN 0-471-56658-6), p. 213–219
- (en) D. A. McQuarrie, Statistical Mechanics, University Science Books, 2000 (ISBN 978-1891389153), p. 91–128
- (en) Richard Tolman, Statistical Mechanics, with Applications to Physics and Chemistry, Chemical Catalog Company, 1927, p. 72–81 ASIN B00085D6OO
Sélection d’articles de périodiques
- (en) JWS Rayleigh, « The Law of Partition of Kinetic Energy », dans Philosophical Magazine, vol. 49, 1900, p. 98–118 [texte intégral]
- (en) Richard C. Tolman, « A General Theory of Energy Partition with Applications to Quantum Theory », dans Physical Review, vol. 11, 1918, p. 261–275 [texte intégral]
- (en) L. Peliti, « On the equipartition of kinetic energy in an ideal gas mixture », dans European Journal of Physics, vol. 28, 2007, p. 249 [texte intégral]
- (en) A. Komar, « Relativistic equipartition », dans General Relativity and Gravitation, vol. 28, 1996, p. 379-385 [texte intégral]
Analyses historiques
- (en) S.G. Brush, The Kind of Motion We Call Heat, North Holland, Amsterdam, 1976 (ISBN 978-0444870094), p. 134–159 (vol. 1) et 336–339 (vol. 2).
Ouvrage de référence en deux volumes sur l’histoire de la théorie cinétique des gaz et de la physique statistique.
- (en) S. Bergia and L. Navarro, « Early quantum concepts and the theorem of equipartition of energy in Einstein’s work (1905-1925) », dans Physis, vol. XXXIV, 1997, p. 183-223 [texte intégral]
Lien externe
- Portail de la physique
Catégories : Bon article | Physique statistique | Théorème de physique
Wikimedia Foundation. 2010.


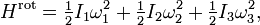
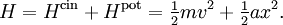
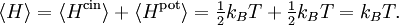
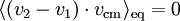
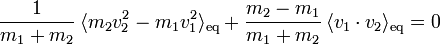
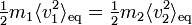
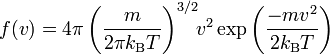
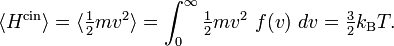
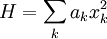
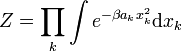
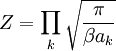
![Z \propto \left[\beta^{-1/2}\right]^f](/pictures/frwiki/102/f8c29c1bbb7129cf1df3f77862767c03.png)
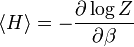
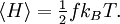
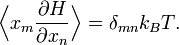
![\langle X \rangle =
\frac{1}{\Gamma} \, \int_{H \in \left[ E, E+\Delta E \right]} X \,\mathrm d\Gamma](/pictures/frwiki/100/dec43fc80db2d217a6ff5d27e5cbf34a.png)
![\int_{H \in \left[ E, E+\Delta E \right]} \ldots \mathrm d\Gamma = \Delta E \frac{\partial}{\partial E} \int_{H < E} \ldots \mathrm d\Gamma,](/pictures/frwiki/53/546c42627e867e56cf1b2edeb2510fc8.png)
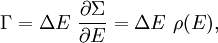
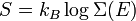
![\Bigl\langle x_{m} \frac{\partial H}{\partial x_{n}} \Bigr \rangle =
\frac{1}{\Gamma} \, \int_{H \in \left[ E, E+\Delta E \right]} x_{m} \frac{\partial H}{\partial x_{n}} \,\mathrm d\Gamma](/pictures/frwiki/52/4275f5de392a2b39f69b882fab4d7b26.png)
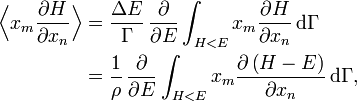
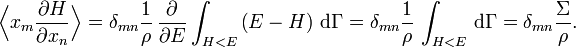
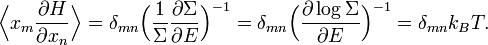
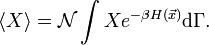
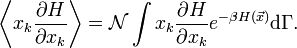
![\left\langle x_k \frac{\partial H}{\partial x_k} \right\rangle =
\mathcal{N} \int \left[ -\frac{1}{\beta} x_k e^{-\beta H(\vec x)}\right]_{x_k=x_{k\mathrm{min}}}^{x_k=x_{k\mathrm{max}}} \mathrm d\Gamma_k
+\mathcal{N}\frac{1}{\beta}\int e^{-\beta H(\vec x)}\mathrm d\Gamma.](/pictures/frwiki/100/d77407e2582d856d2438f39287a3a423.png)
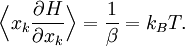
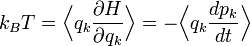
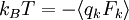
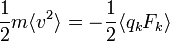
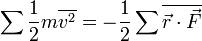
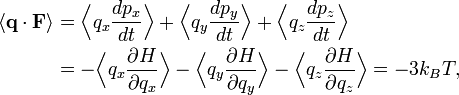
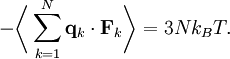
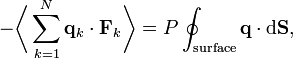

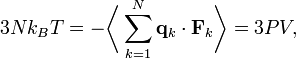
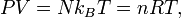
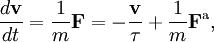
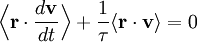
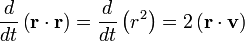
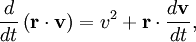
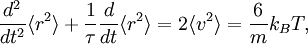
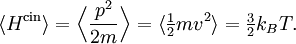
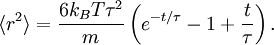
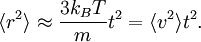
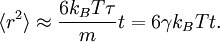
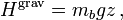
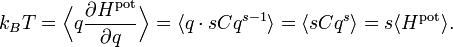
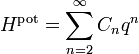
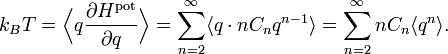
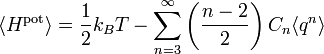
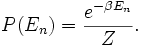
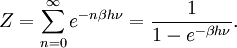
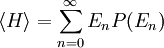
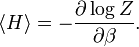
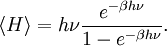
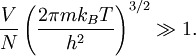
![\frac{\langle E\rangle}{N} = \frac{3}{2}k_B T\left[1-0,1768\, \frac{N}{V}\left(\frac{h^2}{2 \pi m k_B T}\right)^{3/2}\right].](/pictures/frwiki/97/a1725438a673dc8febead8c545abfb84.png)