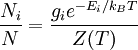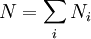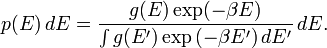Facteur de Boltzmann

Facteur de Boltzmann

Distribution de Boltzmann

En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d'états i qui ont chacun pour énergie Ei :

{{N_i}\over{N}} = {{g_i e^{-E_i/k_BT}}\over{Z(T)}}

où kB est la constante de Boltzmann, T est la température (postulée comme était définie très précisément), gi est la dégénérescence, ou le nombre d'états d'énergie Ei, N est le nombre total de particules :

N=\sum_i N_i\,

et Z(T) est appelée fonction de partition, qui peut être considérée comme égale à :

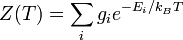Z(T)=\sum_i g_i e^{-E_i/k_BT}.

D'autre part, pour un système simple à température définie de manière exacte, elle donne la probabilité pour le système soit dans l'état spécifié. La distribution de Boltzmann s'applique seulement pour des particules à assez haute température et assez faible densité pour que les effets quantiques soient ignorés, et que ces particules obéissent à la statistique de Maxwell-Boltzmann (se référer à cette article pour la démonstration de la distribution de Boltzmann).
La distribution de Boltzmann est parfois écrite en termes de β = 1/kT où β est le beta thermodynamique. Le terme exp(−βEi) ou exp(−Ei/kT), qui donne la probabilité relative (non normalisée) d'un état, est appelé facteur de Boltzmann et apparaît parfois dans les études en physique et chimie.
Lorsque l'énergie est identifiée à l'énergie cinétique de la particule :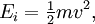

E_i = {\begin{matrix} \frac{1}{2} \end{matrix}} mv^{2},,

la distribution est une distribution de Maxwell-Boltzmann des vitesses de molécules gazeuses, auparavant prédite par Maxwell en 1859. La distribution de Boltzmann est, cependant, plus générale. Par exemple, elle prédit aussi les variations de la densité de particules dans un champ gravitationnel en fonction de la hauteur, si 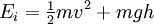E_i = {\begin{matrix} \frac{1}{2} \end{matrix}} mv^{2} + mgh. En fait, cette distribution s'applique dans tous les cas où les considérations quantiques peuvent être ignorées.
Dans certains cas, une approximation continue. S'il existe g(E) dE d'états d'énergie comprise entre E et E + dE, la distribution de Boltzmann prédit la distribution de probabilité pour l'énergie :

p(E)\,dE = {g(E) \exp({-\beta E})\over {\int g(E') \exp {(-\beta E')}}\,dE'}\, dE.

g(E) est appelé densité d'états si le spectre énergétique est continu.
Les particules classiques avec cette distribution d'énergie obéissent à la statistique de Maxwell-Boltzmann. Dans la limite classique, i.e. pour des valeurs élevées de E/kT ou une faible densité d'états— lorsque les fonctions d'ondes des particules ne se superposent pas en pratique, les distributions de Bose-Einstein et de Fermi-Dirac s'identifient à une distribution de Boltzmann.


  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Boltzmann distribution ».
  • Portail de la physique Portail de la physique
Ce document provient de « Distribution de Boltzmann ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Facteur de Boltzmann de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • facteur de Boltzmann — Bolcmano daugiklis statusas T sritis fizika atitikmenys: angl. Boltzmann factor vok. Boltzmann Faktor, m; Boltzmannscher Faktor, m rus. множитель Больцмана, m pranc. facteur de Boltzmann, m …   Fizikos terminų žodynas

  • Boltzmann factor — Bolcmano daugiklis statusas T sritis fizika atitikmenys: angl. Boltzmann factor vok. Boltzmann Faktor, m; Boltzmannscher Faktor, m rus. множитель Больцмана, m pranc. facteur de Boltzmann, m …   Fizikos terminų žodynas

  • Boltzmann-Faktor — Bolcmano daugiklis statusas T sritis fizika atitikmenys: angl. Boltzmann factor vok. Boltzmann Faktor, m; Boltzmannscher Faktor, m rus. множитель Больцмана, m pranc. facteur de Boltzmann, m …   Fizikos terminų žodynas

  • BOLTZMANN (L.) — Physicien et philosophe des sciences, Ludwig Boltzmann est un des penseurs les plus originaux de la seconde moitié du XIXe siècle. Son influence a été profonde sur le développement de la science moderne. Par son interprétation de l’entropie, qui… …   Encyclopédie Universelle

  • Distribution De Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… …   Wikipédia en Français

  • Distribution de boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… …   Wikipédia en Français

  • Equation de Poisson-Boltzmann — Équation de Poisson Boltzmann Pour les articles homonymes, voir Poisson (homonymie). L équation de Poisson Boltzmann est une équation qui apparaît dans la théorie de Debye Huckel des solutions ioniques. Cette équation permet de calculer le… …   Wikipédia en Français

  • Équation de poisson-boltzmann — Pour les articles homonymes, voir Poisson (homonymie). L équation de Poisson Boltzmann est une équation qui apparaît dans la théorie de Debye Huckel des solutions ioniques. Cette équation permet de calculer le potentiel électrostatique créé par… …   Wikipédia en Français

  • Distribution de Boltzmann — En physique, la distribution de Boltzmann prédit la fonction de distribution pour le nombre fractionnaire de particules Ni / N occupant un ensemble d états i qui ont chacun pour énergie Ei : où kB est la constante de Boltzmann, T est la… …   Wikipédia en Français

  • Équation de Poisson-Boltzmann — Pour les articles homonymes, voir Poisson (homonymie). L équation de Poisson Boltzmann est une équation qui apparaît dans la théorie de Debye Huckel des solutions ioniques. Cette équation permet de calculer le potentiel électrostatique créé par… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”