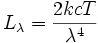Loi De Rayleigh-Jeans

Loi de Rayleigh-Jeans

La loi de Rayleigh-Jeans est une loi proposée au XIX^e siècle par le physicien John William Strutt Rayleigh et le physicien, mathématicien et astronome James Jeans, tous deux anglais, afin d'exprimer la distribution de la luminance spectrale énergétique du rayonnement thermique du corps noir en fonction de la température dans le domaine des grandes longueurs d'ondes.

Cavité électromagnétique

On s'intéresse à l'onde électromagnétique existant dans une cavité parallélépipédique, délimitée par des parois parfaitement conductrices. A l'équilibre thermique à température T, on peut assimiler ce champ au rayonnement d'équilibre. L'étude des ondes stationnaires conduit à une expression de la fréquence mettant en jeu trois nombres entiers positifs (quantification des modes).

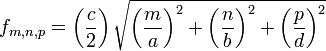
$f_{m,n,p}=\left(\frac{c}{2}\right)\sqrt{\left(\frac{m}{a}\right)^2+\left(\frac{n}{b}\right)^2+\left(\frac{p}{d}\right)^2}$

où a, b et d sont les dimensions de la cavité. Il est possible de donner une représentation dans un huitième d'espace (coordonnées toutes positives) dont les axes sont gradués en 1/a, 1/b et 1/d. Trois entiers positifs m, n et p définissent en effet un mode par un point^[1].

Dénombrement des modes

Pour un intervalle de fréquence $[0,ν]$ , les modes correspondent à des points contenus dans un huitième de sphère de rayon égal à 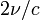$\ 2\nu/c \$ d'après la relation précédente. Dès que le nombre de modes est élevé, il est possible d'en évaluer le nombre en divisant le volume du huitième de sphère par celui d'une cellule élémentaire. Celle-ci est un parallélépipède de côtés 1/a, 1/b et 1/d, donc de volume 1/(abd)=1/V, où V est le volume de la cavité. On aboutit ainsi à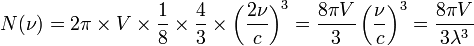

$N(\nu)= 2\pi\times V \times\frac{1}{8}\times\frac{4}{3}\times\left(\frac{2\nu}{c}\right)^3=\frac{8\pi V}{3}\left(\frac{\nu}{c}\right)^3=\frac{8\pi V}{3\lambda^3}$

Pour un intervalle spectral élémentaire $[ν,ν + d ν]$ ou $[λ,λ + d λ]$ , le nombre de modes est ainsi donné par la différentielle de N, soit, au signe près:

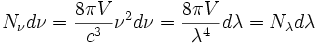
$N_\nu d\nu=\frac{8\pi V}{c^3}\nu^2d\nu=\frac{8\pi V}{\lambda^4}d\lambda =N_\lambda d\lambda$

La densité spectrale des modes est

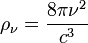
$\rho_\nu=\frac{8\pi\nu^2}{c^3}$

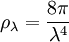
$\rho_\lambda=\frac{8\pi}{\lambda^4}$

Densité spectrale d'énergie

En divisant le nombre de modes N par le volume V et en multipliant par l'énergie thermique kT, on obtient la densité spectrale d'énergie:

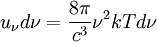
$u_\nu d\nu=\frac{8\pi}{c^3}\nu^2 kT d\nu$

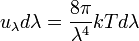
$u_\lambda d\lambda=\frac{8\pi}{\lambda^4}kT d\lambda$

En multipliant par la vitesse de la lumière et en divisant par $4π$ radians, on obtient la luminance spectrale énergétique:

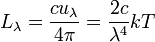
$L_\lambda=\frac{cu_\lambda}{4\pi}=\frac{2c}{\lambda^4}kT$

Formule de Rayleigh-Jeans

La luminance spectrale énergétique est (W/(m³.sr) :

$L_\lambda = \frac{2kc T}{\lambda^{4}}$

avec :

c = 299 792 458 m⋅s^-1 (vitesse de la lumière),

k = 1,38066×10^-23 J⋅K^-1 (constante de Boltzmann),

T est la température de la surface du corps noir en kelvins (K).

Cette loi, qui suggérait une croissance sans limite de la luminance dans le domaine des faibles longueurs d'ondes, n'était pas vérifiée par l'expérience dans l'ultra-violet.

C'est ce qui conduisit Max Planck à proposer une loi valable sur la totalité du spectre : la loi de Planck.

Ainsi, aujourd'hui, la loi de Rayleigh-Jeans n'est plus qu'une approximation de la loi de Planck, utilisable lorsque $λ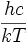$ ≫ $\frac{hc}{kT}$ , avec :

h = 6,62617×10^-34 J⋅s (constante de Planck).

Références

↑ Loi du rayonnement de Rayleigh-Jeans

Voir aussi

Portail de la physique

Ce document provient de « Loi de Rayleigh-Jeans ».

Catégorie : Loi en physique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi De Rayleigh-Jeans de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Loi de rayleigh-jeans — La loi de Rayleigh Jeans est une loi proposée au XIXe siècle par le physicien John William Strutt Rayleigh et le physicien, mathématicien et astronome James Jeans, tous deux anglais, afin d exprimer la distribution de la luminance spectrale… … Wikipédia en Français
Loi de Rayleigh-Jeans — Comparaison de différentes lois de rayonnement (Rayleigh Jeans, Wien et Planck). Les lois de Planck et de Rayleigh Jeans s accordent bien aux plus basses fréquences. Les lois de Planck et de Wien s accordent bien aux plus hautes fréquences. La… … Wikipédia en Français
loi de Rayleigh-Jeans — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
Rayleigh-Jeans equation — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
Rayleigh-Jeans radiant law — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
Rayleigh-Jeans radiation formula — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
Gesetz von Rayleigh-Jeans — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
formule de Rayleigh-Jeans — Reilėjaus ir Džinso spinduliuotės dėsnis statusas T sritis fizika atitikmenys: angl. Rayleigh Jeans equation; Rayleigh Jeans radiant law; Rayleigh Jeans radiation formula vok. Gesetz von Rayleigh Jeans, n; Rayleigh Jeanssches Strahlungsformel, f; … Fizikos terminų žodynas
Loi De Planck — Pour les articles homonymes, voir Planck. La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. La luminance[1] énergétique… … Wikipédia en Français
Loi de planck — Pour les articles homonymes, voir Planck. La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique. La luminance[1] énergétique… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi De Rayleigh-Jeans