Theoreme ergodique

Theoreme ergodique

Théorème ergodique

Dans les systèmes dynamiques, et en particulier en théorie ergodique, de nombreux théorèmes sont appelés théorèmes ergodiques. Ils permettent de quantifier au sens de la théorie de la mesure la densité des orbites d'un système dynamique mesuré.

Sommaire

Théorème ergodique de Birkhoff

Soit :

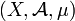  • (X, \mathcal{A},\mu) un espace mesuré.
  • T:X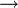\rightarrowX une transformation mesurable.
  • μ une mesure finie T-invariante (c'est à dire que pour tout ensemble mesurable A de 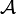\mathcal{A}, on a μ(T − 1(A)) = μ(A)).


Alors :

  • Pour toute fonction f de L1(X,μ), la suite 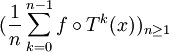(\frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}(x))_{n \geq 1} converge μ-presque sûrement.

De plus, en notant (lorsqu'elle existe), 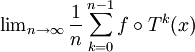\lim\nolimits_{n \to \infty} \frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}(x) = g(x), on a :

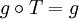  • g \circ T = g; μ-presque sûrement.
  • | | g | | 1 = | | f | | 1 (g est donc dans L1(X,μ)).
  • La suite de fonctions 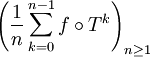\left(\frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}\right)_{n \geq 1} converge dans L1(X,μ) vers g.
  • Pour tout ensemble mesurable A tel que 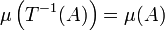\mu \left(T^{-1}(A)\right)=\mu(A), on a :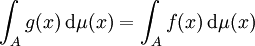\int_{A} g(x)\, \mathrm d\mu(x)= \int_{A} f(x)\, \mathrm d\mu(x)

Corollaire

Avec les mêmes hypothèses et en supposant en plus, que la mesure μ soit ergodique, on a :

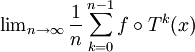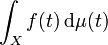\lim\nolimits_{n \to \infty} \frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}(x) =\int_{X} f(t)\, \mathrm d\mu(t) pour μ presque tout x.

Remarques

  • La somme 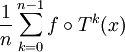\frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}(x) s'appelle une moyenne de Birkhoff de f.
  • La limite 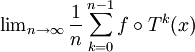\lim\nolimits_{n \to \infty} \frac{1}{n}\sum_{k=0}^{n-1} f\circ T^{k}(x) lorsqu'elle existe s'appelle la moyenne orbitale (ou temporelle) de f.
  • L'intégrale 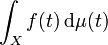\int_{X} f(t)\, \mathrm d\mu(t) est la moyenne spatiale de f.

Ainsi, le théorème dit que si μ est une mesure de probabilité ergodique, presque toutes les moyennes temporelles d'une fonction intégrable coïncident avec sa moyenne spatiale.

Quelques applications simples

  • Exemple 1

Soit B un ensemble mesurable non négligeable (μ(B) > 0). Si μ est ergodique, alors pour presque tous x de X, on a :

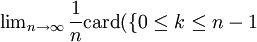\lim\nolimits_{n \to \infty} \frac{1}{n}\operatorname{card}(\{ 0 \leq k \leq n-1 tel que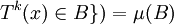 T^{k}(x) \in B \}) = \mu(B)

La proportion de temps que l'orbite de x passe dans B est précisément μ(B).


  • Exemple 2

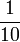Pour presque tout x \in [0,1], le nombre moyen de zéros dans l'écriture décimale de x (c'est-à-dire que x = 0,a1a2a3... où a1 est le chiffre des dixièmes de x, a2 le chiffre des centièmes de x, etc) est égale à \frac{1}{10}.

Théorème ergodique de Von Neumann

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me ergodique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme ergodique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Théorème ergodique — Dans les systèmes dynamiques, et en particulier en théorie ergodique, de nombreux théorèmes sont appelés théorèmes ergodiques. Ils permettent de quantifier au sens de la théorie de la mesure la densité des orbites d un système dynamique mesuré.… …   Wikipédia en Français

  • ERGODIQUE (THÉORIE) — Ergodique vient du mot grec 﨎福塚礼益 qui signifie travail. C’est en effet d’un problème de mécanique que la théorie ergodique est issue. À l’origine se trouve une hypothèse de la théorie cinétique des gaz, audacieusement posée par L. Boltzmann en… …   Encyclopédie Universelle

  • ergodique — ● ergodique adjectif (allemand Ergoden, grec hodos, chemin) Se dit, pour un processus aléatoire stationnaire, d une hypothèse selon laquelle les caractéristiques statistiques, déduites des valeurs moyennes calculées à partir des valeurs à un même …   Encyclopédie Universelle

  • Théorème de Birkhoff — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Théorèmes nommés d après George David Birkhoff Théorème ergodique de Birkhoff Théorème de Poincaré Birkhoff, affirmant que toute application d un anneau… …   Wikipédia en Français

  • Théorème de von Neumann — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. De nombreux théorèmes de mathématiques ou de physique théorique portent le nom de John von Neumann, parmi lesquels : le théorème du bicommutant de… …   Wikipédia en Français

  • Theoreme de recurrence de Poincare — Théorème de récurrence de Poincaré Le théorème de récurrence de Poincaré (1890) dit que, pour presque toutes les « conditions initiales », un système dynamique conservatif dont l espace des phases est de « volume » fini va… …   Wikipédia en Français

  • Théorème de récurrence — de Poincaré Le théorème de récurrence de Poincaré (1890) dit que, pour presque toutes les « conditions initiales », un système dynamique conservatif dont l espace des phases est de « volume » fini va repasser au cours du temps …   Wikipédia en Français

  • Théorème de récurrence de poincaré — Le théorème de récurrence de Poincaré (1890) dit que, pour presque toutes les « conditions initiales », un système dynamique conservatif dont l espace des phases est de « volume » fini va repasser au cours du temps aussi près… …   Wikipédia en Français

  • Theoreme de Liouville (Hamiltonien) — Théorème de Liouville (Hamiltonien) Pour les articles homonymes, voir Théorème de Liouville. En physique, le théorème de Liouville, nommé d après le mathématicien Joseph Liouville, est un théorème utilisé par le formalisme hamiltonien de la… …   Wikipédia en Français

  • Théorème de liouville (hamiltonien) — Pour les articles homonymes, voir Théorème de Liouville. En physique, le théorème de Liouville, nommé d après le mathématicien Joseph Liouville, est un théorème utilisé par le formalisme hamiltonien de la mécanique classique, mais aussi en… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”