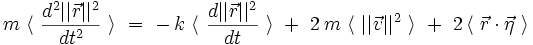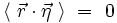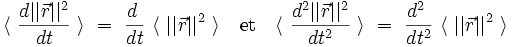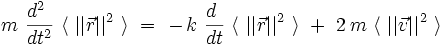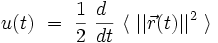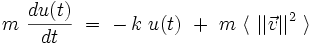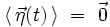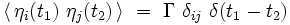- Equation de Langevin
-
Équation de Langevin
L'équation de Langevin (1908) est une équation stochastique pour le mouvement brownien.
Sommaire
Théorie de Langevin du mouvement brownien
Dans l'approche théorique de Langevin, une grosse particule brownienne de masse m, supposée animée à l'instant t d'une vitesse
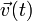 , est soumise à deux forces bien distinctes :
, est soumise à deux forces bien distinctes :- une force de frottement fluide du type
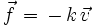 , où k est une constante positive. Dans le cas d'une particule sphérique de rayon a, cette constante s'écrit explicitement : k = 6πηa (loi de Stokes).
, où k est une constante positive. Dans le cas d'une particule sphérique de rayon a, cette constante s'écrit explicitement : k = 6πηa (loi de Stokes).
- une force complémentaire, notée
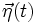 , qui synthétise la résultante des chocs aléatoires des molécules de fluide environnantes. Langevin écrit à propos de cette force supplémentaire qu' « elle est indifféremment positive et négative, et sa grandeur est telle qu'elle maintient l'agitation de la particule que, sans elle, la résistance visqueuse finirait par arrêter ». On appelle au XXIe siècle une telle force un bruit blanc gaussien[1].
, qui synthétise la résultante des chocs aléatoires des molécules de fluide environnantes. Langevin écrit à propos de cette force supplémentaire qu' « elle est indifféremment positive et négative, et sa grandeur est telle qu'elle maintient l'agitation de la particule que, sans elle, la résistance visqueuse finirait par arrêter ». On appelle au XXIe siècle une telle force un bruit blanc gaussien[1].
Équation de Langevin
On applique le principe fondamental de la dynamique de Newton, ce qui conduit à l'équation stochastique de Langevin :
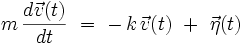
Solution de Langevin (1908)
Réécriture de l'équation de Langevin
Prenons le produit scalaire de cette équation avec le vecteur position
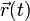 (en omettant la dépendance en temps pour simplifier les notations) :
(en omettant la dépendance en temps pour simplifier les notations) :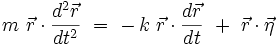
Remarquons alors d'une part que :
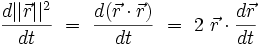
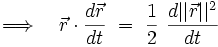
et d'autre part que :
![\frac{ d^2 ||\vec{r}||^2 }{ dt^2 } \ = \ \frac{d~}{dt} \ \left[ \frac{ d ||\vec{r}||^2}{dt} \right] \ = \ \frac{d~}{dt} \ \left[ \, 2 \ \vec{r} \cdot \frac{d\vec{r}}{dt} \, \right] \ = \ 2 \, ||\vec{v}||^2 \ + \ 2 \ \vec{r} \cdot \frac{d^2\vec{r}}{dt^2}](/pictures/frwiki/56/8a5c13bf8640582753317211d6807f0e.png)
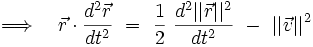
En substituant ces expressions dans le produit scalaire obtenu à partir de l'équation de Langevin, on obtient une nouvelle forme de l'équation différentielle :
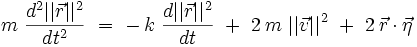
Moyenne sur le bruit blanc gaussien
On prend alors la moyenne de l'équation précédente sur toutes les réalisations possibles du bruit blanc gaussien. Il vient :
On fait l'hypothèse avec Langevin que la valeur moyenne du terme de bruit est nulle[2] :
Par ailleurs, le processus de moyenne sur le bruit commute avec la dérivation temporelle :
ce qui conduit à l'équation différentielle pour les moyennes :
On pose alors :
de telle sorte que l'équation différentielle se réécrive sous la forme simple :
Équipartition de l'énergie
On obtient une estimation du dernier terme de vitesse quadratique moyenne en utilisant le théorème d'équipartition de l'énergie de la physique statistique classique[3]. Pour le mouvement d'une particule dans un espace à d dimensions, on obtient :
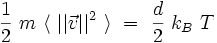
où kB est la constante de Boltzmann, et T la température absolue en kelvins. L'énergie thermique moyenne kBT par particule peut se réécrire :
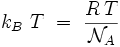
où R est la constante des gaz parfaits, et
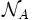 le nombre d'Avogadro. L'équation différentielle se met donc finalement sous la forme :
le nombre d'Avogadro. L'équation différentielle se met donc finalement sous la forme :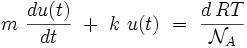
Cette équation différentielle linéaire du premier ordre à coefficients constants avec second membre admet la solution exacte :
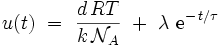
où λ est une constante, et τ le temps caractéristique de relaxation, qui vaut :
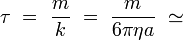 10-8 secondes
10-8 secondesdans les conditions d'observations expérimentales usuelles du mouvement brownien.
Coefficient de diffusion d'Einstein
Dans les conditions expérimentales usuelles, on est toujours dans le régime où :
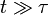 , et on observe alors :
, et on observe alors :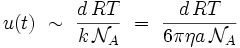
Compte-tenu de la définition de u(t), on a :
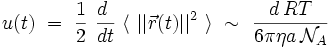
ce qui donne par intégration par rapport au temps t la loi de la diffusion classique :
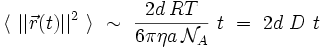
où le coefficient de diffusion D s'écrit explicitement :
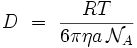
On retrouve bien le résultat d'Einstein (1905).
Solution moderne
Cf. l'article de Bertrand Duplantier, paragraphe 1.5.3 , p. 177.
Articles connexes
Bibliographie
- Paul Langevin ; Sur la théorie du mouvement brownien, Comptes-Rendus de l'Académie des Sciences 146 (1908), 530-532. Possibilité de consulter et de télécharger le texte complet depuis le site Gallica de la Bibliothèque nationale de France : format pdf .
- Bertrand Duplantier ; Le mouvement brownien, (2005), dans : Séminaire Poincaré Einstein, 1905-2005, (Paris, 8 avril 2005). Texte complet disponible ici.
Notes et références
- ↑ En termes modernes, un bruit blanc gaussien est un processus stochastique de moyenne nulle :
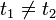 Dans ces deux formules, la moyenne est prise sur toutes les réalisations possibles du bruit blanc gaussien.
Dans ces deux formules, la moyenne est prise sur toutes les réalisations possibles du bruit blanc gaussien. - ↑ Langevin écrit :
Ce n'est en réalité pas si évident que cela ; lire par exemple l'article de Bertrand Duplantier, page 176, note 52. Cet auteur donne un peu plus loin dans le même article la dérivation moderne de la solution de l'équation stochastique de Langevin (paragraphe 1.5.3 , p. 177).« La valeur moyenne du terme
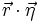 est évidemment nulle à cause des irrégularités des actions complémentaires
est évidemment nulle à cause des irrégularités des actions complémentaires 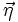 . »
. » - ↑ Le théorème d'équipartition de l'énergie de la mécanique statistique classique dit que la valeur moyenne de l'énergie associée à un degré de liberté \emph{quadratique} d'un système mécanique en équilibre thermique avec un thermostat à la température T est égale à kBT / 2. Pour une particule ponctuelle qui n'est soumise à aucune force dans un espace à d dimensions, il y a exactement d degrés de liberté \emph{quadratiques}, qui correspondent aux d contributions à l'énergie cinétique :
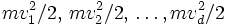 , d'où le résultat utilisé ici.
, d'où le résultat utilisé ici.
- Portail des mathématiques
- Portail de la physique
Catégories : Processus stochastique | Physique statistique - une force de frottement fluide du type
Wikimedia Foundation. 2010.