Oscillateur harmonique

Un oscillateur harmonique est un oscillateur dont l'évolution au cours du temps est décrite par une fonction sinusoïdale et dont la fréquence ne dépend que des caractéristiques du système. L'intérêt d'un tel modèle est qu'il décrit l'évolution de n'importe quel système physique au voisinage d'une position d'équilibre stable, ce qui en fait un outil transversal utilisé dans de nombreux domaines : mécanique, électricité et électronique, optique.

Dans la pratique, de tels oscillateurs ne sont que des cas idéaux pour lesquels les forces dissipatives (frottement par exemple) sont négligées. Pour que leur amplitude reste constante, il est nécessaire d'entretenir les oscillations en fournissant de l'énergie.

Oscillateurs mécaniques

Oscillations de translation

Oscillation verticale

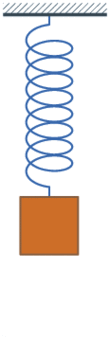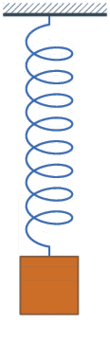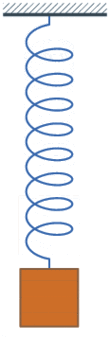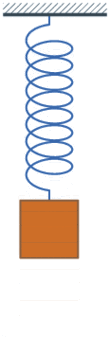
On peut mettre en oscillation une masse soumise à l'action d'un ressort. On peut suivant les cas, réaliser des oscillations verticales ou des oscillations horizontales (en utilisant un dispositif permettant de minimiser les frottements sur le support).

Dans les deux cas, les oscillations sont harmoniques : la fonction du temps x(t) de la position de la masse de part et d'autre de la position d'équilibre (statique) est une fonction sinus. La période est indépendante de l’amplitude (isochronisme des oscillations) : elle ne dépend que de l'inertie du système (masse m) et de la caractéristique de la force de rappel (constante de raideur k du ressort) :

La constante de raideur k est exprimée en N/m. Pour k = 1 N/m, il faudrait un Newton pour allonger le ressort d'un mètre. En réalité, la période dépend aussi de la masse du ressort, qui est négligée dans la formule ci-dessus. Voir l'article détaillé : système masse-ressort, pour une théorie plus complète.

Si les oscillations sont amorties par une force de frottement fluide (type visqueux à faible vitesse, force en − αv ), l'équation différentielle du mouvement peut s'écrire :

Oscillations de rotation

Schéma d'un pendule de torsion

Le dispositif est constitué d'une barre horizontale fixée à un support par l'intermédiaire d'un fil de torsion : ce fil d'acier exerce un couple de rappel proportionnel à l'angle de torsion qu'on lui impose : . Sur la barre on peut positionner deux masselottes de façon symétrique de façon à modifier le moment d'inertie.

La période est indépendante de l’amplitude (isochronisme des oscillations). Elle est donnée par la relation ci-dessous où J désigne le moment d'inertie de la barre munie des masselottes.

Équation différentielle :

L'oscillateur harmonique comme modèle

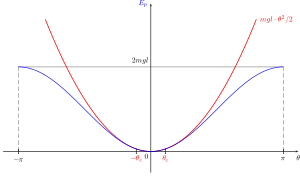
Les oscillateurs ne sont généralement pas harmoniques. Mais, dès que l'énergie potentielle d'un système à une dimension possède un minimum en un point, on peut l'approximer par l'énergie potentielle d'un oscillateur harmonique au voisinage de ce point. Il faut simplement s'assurer que les oscillations autour de ce point sont suffisamment petites pour que l'approximation du puits de potentiel par une parabole soit valide.

Pendule simple

Lorsque les oscillations sont de faible amplitude (lorsque sin(θ) peut être approximé à θ), l'erreur commise en approximant le puits de potentiel par une parabole est faible. À titre d'exemple, pour des oscillations telles que l'angle θ entre la position du pendule et la verticale est de l'ordre de 20°, l'erreur est de 1 %.

potentiel d'un pendule simple et son approximation parabolique

L'équation du mouvement peut être alors simplifiée et mise sous la forme :

avec

d'où une période propre .

Oscillateurs électriques

Circuit LC

Un circuit LC en électrocinétique est un circuit théorique comportant une bobine idéale : parfaitement inductive (inductance L et résistance nulle) et un condensateur (capacité C). Les deux dipôles sont en outre totalement linéaires, ce qui est le cas avec des bobines à noyau d'air mais qui ne l'est pas pour de bobines avec un noyau ferromagnétique.

Un tel circuit se comporte alors comme un oscillateur dont la période propre est  :

De la loi des mailles : , et des équations caractéristiques des deux dipôles : et , on déduit :

, avec

L'équation différentielle peut donc s'écrire :

Circuit RLC

Dans un circuit LC réel, on ne peut s'affranchir de la résistance. Celle-ci dissipe de l'énergie par effet joule. Dans ce cas, l'équation différentielle qui régit les oscillations (amorties) peut s'écrire :

Remarque : on peut entretenir les oscillations grâce à un montage dit à résistance négative.

Analogie électro-mécanique

Les oscillations mécaniques avec amortissement fluide, et les oscillations électriques d'un circuit RLC conduisent à deux équations différentielles du second ordre formellement identiques.

Oscillateur générique	RLC	Masse soumise à un ressort
	V = tension	F = Force
z	q = charge électrique	x = déplacement
	= intensité	= vitesse
		= accélération
β	L = inductance propre	m = masse du mobile
ρ	R = résistance	α = coef de frottement
γ	= inverse de la capacité	k = constante de raideur
= période propre	= période propre	= période propre
f	P = RI2 : effet Joule	: force de frottement
Q = facteur de qualité

Oscillateurs électriques entretenus

On obtient des oscillations électriques entretenues en associant un élément amplificateur, à un circuit LC. L'énergie est prélevée sur le circuit LC, amplifiée puis réinjectée sur le même circuit, tout cela par des couplages adéquats. L'oscillation a lieu lorsque les pertes du circuit LC sont compensées par l'énergie réinjectée par l'amplificateur. L'étude théorique peut être réalisée en considérant deux quadripoles bouclés l'un sur l'autre: Le quadripôle amplificateur et le circuit LC considéré comme un quadripôle filtre.

Différents montages pratiques d'oscillateurs ont été proposés : oscillateur Colpitts, oscillateur Clapp, oscillateur Hartley, oscillateur de Pierce.

Ces oscillateurs entretenus peuvent inclure un quartz, qui permet d'obtenir une meilleure stabilité de fréquence. Les oscillateurs entretenus sont très utilisés en électronique par exemple, pour les horloges des circuits numériques, ou pour les pilotes des appareils de télécommunications.

Articles connexes

• Systèmes oscillants à un degré de liberté
• Oscillateur harmonique quantique
• Oscillations amorties

Bibliographie

• Vladimir Damgov, Nonlinear and parametric phenomena. Applications in radiometric and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.

• Portail de la physique