Pythagor

Pythagore

Pythagore, détail de l'École d'Athènes de Raphaël, 1509
Naissance	-580 Samos (Grèce)
Décès	-497 Métaponte (Basilicate)
Champs	Éthique, mathématiques, métaphysique, musique, politique
Institution	École pythagoricienne
Célèbre pour	Gamme pythagoricienne, Harmonie des sphères, Nombre d'or, Théorème de Pythagore
modifier

Pythagore (en grec ancien Πυθαγόρας / Pythagóras) serait né aux environs de 580 av. J.-C. à Samos, une île de la mer Egée au Sud-Est de la ville d'Athènes ; on établit sa mort vers 497 av. J.-C., à l'âge de 83 ans.

Le nom de Pythagore ou Pyth-agore, étymologiquement « celui qui a été annoncé par la Pythie », découle de l'annonce de sa naissance faite à son père lors d'un voyage à Delphes.

La vie énigmatique de Pythagore permet difficilement d'éclaircir l'histoire de ce réformateur religieux, mathématicien, philosophe et thaumaturge. Il exerça une influence immense qui fit basculer la Grèce antique d'un mode de pensée religieux à un mode de pensée rationnel.^{[réf. nécessaire]}

Le néopythagorisme est néanmoins empreint d'une mystique des nombres, déjà présente dans la pensée de Pythagore. Hérodote le mentionne comme « l'un des plus grands esprits de la Grèce, le sage Pythagore »^[1]. Il conserve encore aujourd'hui un grand prestige à tel point que Hegel disait qu'il était « le premier maitre universel »^[2].

D'après un écho marquant d’Héraclide du Pont, Pythagore serait le premier penseur grec à s’être qualifié lui-même de « philosophe »^[3]. Cicéron évoque l'anecdote célèbre sur la création du mot φιλόσοφος : « amoureux de la sagesse », par Pythagore :

« La philosophie (...) était la connaissance des choses divines et humaines, des principes et des causes de chacune d'elles. (...) Ce nom fut courant jusqu'à l'époque de Pythagore ; celui-ci, vint, dit-on, à Phlionte, où il eut des discussions savantes avec Léon, le souverain de Phlionte. Et comme Léon admirait son génie et son éloquence, il lui demanda sur quel art il s'appuyait ; Pythagore répondit qu'il ne connaissait pas un seul art, mais qu'il était philosophe ; Léon s'étonna de ce mot nouveau et lui demanda qui étaient les philosophes. »

— Cicéron,Tusculanes, V, 3, § 8

Biographie de Pythagore

Beaucoup de documents, tardifs, ont été publiés sur la vie de Pythagore^{[4],[5],[6],[7]}. Des chercheurs, dont Eduard Zeller^[8] et André-Jean Festugière, contestent en particulier les voyages en Égypte et en Chaldée.

Naissance

Pythagore naît à Samos en -569 ou -606 selon Ératosthène et Diogène Laërce, en -590 selon Jamblique, en -580 selon Porphyre^[9], et il meurt en -494 ou -497 à Métaponte, en Italie.

Son père, Mnésarque^[10], ciseleur de bagues, et sa mère, Parthénis, la plus belle des Samiennes, descendraient tous deux du héros Ancée, fils de Zeus, qui avait fondé la ville de Samos. Ce Mnésarque de Samos interroge la Pythie de Delphes sur un voyage et obtient une réponse selon laquelle :

« sa femme était enceinte et mettrait au monde un enfant qui l'emporterait en beauté et en sagesse. De ce moment, il changea le nom de sa femme de « Parthénis » en « Pythaïs » [la pythienne], il appela son fils « Pythagore » [Πυθαγόρας, « prédit par la Pythie », ou « annoncé par le dieu pythien », pour la raison qu'il avait été annoncé par le dieu pythien]. »

— Jamblique, Vie de Pythagore, § 7.^[6]

Plus tard, Pythagore affirme qu'il est la réincarnation d'Aithalidès (fils d'Hermès), d'Euphorbe (héros de la guerre de Troie), d'Hermotime de Clazomènes (chamane apollinien), et de Pyrrhos (un pêcheur de Délos), et qu'il se souvenait de ces incarnations antérieures^[4],[5].

Adolescence et maturité

Pythagore est un athlète^[11]. Selon une tradition, Pythagore participe aux jeux Olympiques à l'âge de 17 ans. Ce serait la 57^e olympiade (-552) (et non la 48°^e, -588, selon Ératosthène). Il remporte toutes les compétitions de pugilat^[12] (sport de l'Antiquité comparable à la boxe).

Les sources divergent sur le nombre d'enfants qu'il aurait eu de Théanô : deux ou quatre. Les noms cités sont : Télaugès (qui succéda à son père et qui, selon certains, enseigna à Empédocle), Mnésarque, Myïa (qui épousa Milon de Crotone), Arignotè^[5].

Instruction

Première initiation. À 18 ans, en -551, il quitte Samos. Il va s'instruire à Lesbos auprès de Phérécyde de Syros (vers -585/-499)^[4],[5], un sage, le premier à avoir dit que « les âmes des hommes sont éternelles »^[13] le premier à enseigner que l'homme a deux âmes, l'une d'origine terrestre, l'autre d'origine divine ; un magicien, aussi, qui fait des prédictions, reçoit des songes^[14]. Que les philosophies se ressemblent, c'est sûr ; que les hommes se soient rencontrés, c'est incertain, mais la théorie de l'âme immortelle, individuelle de Phérécyde autorise la théorie pythagoricienne de la transmigration (παλιγγενεσία) des âmes.

Ensuite, les biographes se plaisent à le doter de toutes les initiations possibles auprès des initiés de l'époque et dans les Mystères. Il rencontrerait « les descendants du prophète et naturaliste Môkhos » et les hiérophantes de Phénicie, les hiérogrammates d'Égypte, les Mages de Chaldée, les initiés du mont Ida, les orphiques de Thrace, les prêtresses de Delphes.

Deuxième initiation, en « Syrie » ou « Phénicie ». Il rencontre les descendants du prophète et naturaliste Môkhos de Sidon. Il fréquente des hiérophantes. Il se fait initier à Tyr et à Byblos et ailleurs^[6]. Il revient à Samos, une première fois, suivre les enseignements d'Hermodamas de Samos, un lettré en matière homérique^[4],[5].

Troisième initiation. Dès Hécatée d'Abdère, les historiens soutiennent que Pythagore part en Égypte vers -547, vers Memphis et Diospolis (Thèbes d'Égypte), pour plusieurs années^[15],[5]. Dans cette ville se trouve le sanctuaire de Zeus Ammon. Il est reçu par les prêtres, sous Amasis, pharaon de -568 à -526 et connu de Polycrate de Samos^[16]. Il apprend la langue à Memphis dans un centre d'interprétariat fondé par Psammétique Ier (pharaon en -663). Il étudie la géométrie, l'astronomie des Égyptiens. Il est initié aux Mystères de Diospolis et à la doctrine de la résurrection d'Osiris ; selon Plutarque, les prêtres lui auraient appliqué sur la cuisse le disque ailé d'Atoum-Râ, en feuille d'or, ce qui lui valut le surnom de Pythagore « chrysomère', à la cuisse d'or »^[17].

Quatrième initiation. Certaines traditions ajoutent qu'il est expulsé comme esclave ou prisonnier d'Égypte à Babylone, par Cambyse II, roi de Perse venu conquérir l'Égypte en -525^[18]. Il serait alors allé « chez les Chaldéens et les Mages ». Cet épisode est beaucoup moins attesté que le voyage en Égypte, et les dates posent problème, surtout quand Antiphon prétend que Pythagore est resté 22 ans en Égypte (de -547 à -525 ?) et 12 ans à Babylone (de -525 à -513 ?)^[5]. Il est impossible qu'il ait rencontré Zoroastre (comme le voudrait Porphyre), car le prophète iranien enseignait en -594 environ.

Cinquième initiation : Pythagore se rend en Crète, dans l'antre de l'Ida, haut lieu ésotérique, sous la conduite, dit-on, d'Épiménide de Crète, et des initiés du Dactyle (magicien), Morgès^[4],[5]. Cinquième initiation : il va en Thrace, pour rencontrer les orphiques.

Sixième initiation : il rencontre « Thémistocléa, la prêtresse de Delphes »^[4],[5].

Parcours et mort

Il revient à Samos une seconde fois. Il commence à enseigner dans un amphithéâtre à ciel ouvert, l'Hémicycle, sans grand succès.

Grande-Grèce en 280 av. J.-C.

Banni par Polycrate, « tyran » de Samos de -535 à -522, ou bien fuyant, selon Aristoxène, « la tyrannie de Polycrate »^[19], il quitte Samos vers -535, il part avec son vieux maître Hermodamas. Il va en Grande-Grèce et débarque à Sybaris, ville riche et voluptueuse sur le golfe de Tarente.

Il préfère s'installer à Crotone, toujours sur le golfe de Tarente, en Calabre, car la ville a un culte pour Apollon et une école de médecine célèbre.Le célèbre athlète Milon de Crotone, six fois champion aux jeux Olympiques^[20], et prêtre d'Héra Lacinia, épouse sa fille, Myïa. Son influence sur Crotone s'étend de l'assemblée aux enfants en passant par les adolescents et les femmes qui venaient tous l'écouter. Il ne donne sans doute pas des lois aux Crotoniates, mais il appuie un régime politique de type oligarchique, c'est-à-dire « aristocratique », réservé à une élite. Antidémocrate, il pense que « c'est une chose insensée de tenir compte de l'opinion du grand nombre »^[6]. Les 300 disciples administrent la cité^[4]. Ses conférences publiques attirent 600 personnes. Les Crotoniates l'identifient à Apollon Hyperboréen^[21]. Cette influence à Crotone est l'occasion pour Porphyre de Tyr^[5] de donner une présentation enthousiaste de Pythagore :

« Les citoyens de Crotone comprirent qu'ils avaient affaire à un homme qui avait beaucoup voyagé, un homme exceptionnel, qui tenait de la Fortune de nombreux avantages physiques : il était, en effet, noble et élancé d'allure et, de sa voix, de son caractère et de tout le reste de sa personne émanaient une grâce et une beauté infinies. »

Il fonde son école à Crotone en -532^[6]. C'est une communauté, quasiment une secte, à la fois philosophique, scientifique, politique, religieuse, initiatique. Il fonde d'autres communautés dans les villes d'Italie et de Grèce : Tarente, Métaponte, Sybaris, Caulonia, Locres, et, en Sicile, Rhégium, Tauroménium, Catane, Syracuse. Il ne semble pas qu'il veuille fonder une fédération politique des cités du golfe de Tarente (Tarente, Métaponte, Sybaris, Crotone, dans le talon de la botte Italie). À Crotone, il ferait la rencontre d'Abaris le Scythe, grand magicien et « chamane ».

En -510, une révolution populaire à Sybaris, sous la conduite d'un orateur démocrate, Télys, massacre des pythagoriciens, et 500 aristocrates, se réfugient à Crotone. Une guerre s'ensuit entre Sybaris et Crotone, recommandée - selon Diodore de Sicile - par Pythagore. L'aristocratie de Crotone, sous la conduite de Milon de Crotone, l'emporte avec 100 000 hommes contre 300 000 : elle massacre à son tour la population et rase Sybaris^[22].

Il s'inquiète du progrès du parti démocratique. « Il annonça à ses disciples qu'un soulèvement allait éclater »^[23], et de partir - selon Aristoxène - pour Métaponte, port de la Lucanie, toujours sur le golfe de Tarente. Sans doute il y trouve une communauté pythagoricienne déjà installée. Il a des disciples qui deviennent illustres, dont le médecin Alcméon de Crotone, le mathématicien Hippase de Métaponte^[4],[6]. Les habitants de Métaponte appelaient sa maison « le temple de Déméter », et sa ruelle « temple des Muses ».

Peut-être, en -499, il va enterrer à Délos, grand centre religieux, son vieux maître Phérécyde de Syros^[24].

Pythagore meurt à Métaponte en -497. Cicéron témoigne : « Je suis allé avec toi à Métaponte. Je n'ai pas accepté de me rendre chez notre hôte avant d'avoir vu le lieu où Pythagore est mort et où il avait son siège. »^[25]

Entre -440 ou -454, vers -450, se produit une émeute anti-pythagoricienne, amalgamée par certains historiens à la guerre pro-pythagoricienne de -510. Un noble de Crotone, Cylon de Crotone, gouverneur de Sybaris, fomente un complot. Il veut se venger de Pythagore qui l'aurait jugé inapte à suivre les enseignements de l'école. Il soulève la population contre les pythagoriciens, partisans d'un régime aristocratique et conservateur. Le feu est mis à la maison de Milon de Crotone où sont réunis 40 pythagoriciens. Deux seulement réussissent à se sauver : Lysis de Tarente et Archippe de Tarente, ou Lysis et Philolaos^[26],[5],[6]. Ces persécutions conduisent à la dispersion des membres de l'école pythagoricienne, qui fonde des centres ailleurs, surtout à Rhegium, Phlionte et Thèbes de Lucanie^[27]. Le déclin de l'influence pythagoricienne en Italie commence. Le dernier bastion fut Tarente, avec Archytas de Tarente, stratège, philosophe, mathématicien, inventeur, mais aussi ami et sauveur de Platon en -388 et -361. Les autres versions de la mort de Pythagore semblent douteuses : Diogène Laërce et Porphyre soutiennent que Pythagore serait mort dans l'incendie de la maison de Milon, Hermippe de Smyrne déclare que Pythagore aurait été tué par les Syracusiens, lors de sa fuite, devant un champ de fèves qu'il refusait, par tabou des fèves, de traverser^[4].

La légende (surtout chez Porphyre et Jamblique) attribue à Pythagore des pouvoirs merveilleux : il apprivoise une ourse, à Olympie il fait descendre un aigle du ciel, il connaît ses existences antérieures, il prédit la révolution à Crotone, il devine la quantité de poissons que vont ramener des pêcheurs, il charme et guérit par sa musique, il entend l'harmonie des sphères célestes, il commande à la grêle et aux vents, etc. Bien entendu, il est donné comme expert en arithmologie (art occulte des nombres), arithmosophie (connaissance ésotérique des nombres), arithmomancie (divination par les nombres) : "Grâce aux nombres en question, il pratiquait une admirable méthode de prédiction, et il rendait un culte aux dieux selon les nombres, parce que la nature du nombre leur est complètement apparentée"^[6],[28]. À l'époque hellénistique, l'adjectif "pythagoricien" (πυθαγόρειος) finit par signifier "occultiste, ésotériste, magicien"^[29] Même le sobre Aristote l'admet : "Pythagore avant tout œuvra durement dans les sciences mathématiques et autour des nombres, mais plus tard il lui arriva de ne pas savoir renoncer à la pratique miraculeuse de Phérécyde [de Syros]."^[30].

La communauté pythagoricienne

L'école pythagoricienne de Crotone devint par la suite une hétairie (εταιρεία = confrérie)^[6] politique de courant aristocratique^[31].

Il s'agit d'une fraternité philosophique, religieuse et scientifique, proche de l'orphisme. On dirait aujourd'hui un Ordre, au sens où la Franc-Maçonnerie ou la Rose-Croix sont des Ordres.

La communauté s'échelonne sur quatre degrés initiatiques et hiérarchiques^[6], comme dans de nombreuses organisations initiatiques. Les femmes et les étrangers sont admis. Les profanes (bébêloi) sont "les gens du dehors" (oi exô, οί έξω), les gens du commun, auxquels rien n'est révélé.

Premier degré : les postulants

Pythagore observe, chez ceux qui se présentent comme candidats, les traits du visage (physiognomonie) et les gestes (kinésique)^[5], mais aussi les relations avec les parents, le rire, les désirs, les fréquentations. On est admis ou pas^[6].

Deuxième degré : les néophytes

Leur période de probation dure trois ans, pendant laquelle Pythagore examine la persévérance, le désir d'apprendre. Au terme ils sont refusés ou acceptés. Acceptés, ils prononcent le serment de silence^[32] :

« Non, par celui [Pythagore] qui a trouvé la tétraktys de notre sagesse,
Source qui contient en elle les racines de la nature éternelle. »

Troisième degré : les acousmaticiens

Les acousmaticiens - ou acousmatiques - (άκουσματικοί : "auditeurs"). Ils reçoivent un enseignement de cinq ans, donné sous forme de préceptes oraux (άκούσματα), sans démonstration, destinés à être gardés en mémoire ; par exemple : "Ne pas avoir sur les dieux des opinions ou des paroles hâtives". Ces cinq ans sont cinq ans de silence. Les auditeurs sont devant le rideau derrière lequel Pythagore se dissimule. Ils mettent leurs biens en commun^[33].

Postulants, néophytes et auditeurs forment le grade des "exotériques" (έξωτερικοί) ou novices.

Quatrième et dernier degré : les mathématiciens

Les mathématiciens (μαθηματικοί "savants") ou "ésotériques" ou sindonites (habillés de lin). "Ils devenaient des ésotériques (έσωτερικοί)"^[6], dans la mesure où ils accèdent à la connaissance intérieure, cachée. Ils sont admis à voir Pythagore derrière son rideau. Lui-même enseigne sous forme de "symboles" (σύμβολα), au sens de formules codées, qui sont démontrées ; par exemple : "Ne pas toucher un coq blanc". D'après Photius^[34] on voit une division des "ésotériques" en "vénérables" (sebastikoi σεβαστικοί), "politiques" (politikoi), "contemplatifs". Les vénérables ou pieux s'occupent de religion. Les politiques s'intéressent aux lois, aux affaires humaines, tant dans la communauté pythagoricienne que dans la cité. Les "contemplatifs" étudient arithmétique, musique, géométrie, astronomie : les quatre sciences selon Archytas, qui formeront le quadrivium du Moyen-Âge. Il faudrait ajouter les physiciens ou naturalistes (φυσικοί), qui se penchent sur les sciences concrètes : géographie, météorologie, médecine, mécanique... mais aussi grammaire, poésie... Il est plus vraisemblable que les "acousmaticiens" soient des "politiques, administrateurs ou législateurs" et les 'mathématiciens" des "pieux" ou "contemplatifs"^[6].

De nombreuses règles, pour ne pas dire tabous, s'imposent à celui qui adopte "la vie pythagorique" (βίος πυθαγορικός)^[6].

• règles diététiques (végétarisme sélectif)^[35] : interdiction de manger du rouget, le cœur, le cerveau, la moelle, les fèves, les oeufs... bref tout ce qui symbolise la vie. La consommation de la chair des animaux sacrifiés semble autorisée, sans doute par concession à la religion officielle
• rites religieux : sacrifices non sanglants et sans feu, "honorer les dieux", éviter bouchers et chasseurs, culte "aux dieux farine, miel, fruits, fleurs et autres produits de la terre"^[36], "purifications, ablutions et aspersions" et onctions lustrales...
• exercices spirituels : respect de soi-même, examen de conscience chaque soir^[37], continence sexuelle, "exercer sa mémoire", "chanter en s'accompagnant de la lyre", lire des livres édifiants ensemble...
• exercices physiques^[5],[6] : gymnastique, athlétisme, promenade à deux ou trois, danse...
• objets sacrés : "vêtements blancs" de lin (mais pas de laine, animale), signes de reconnaissance (le pentagramme), symboles (la tétraktys)...

La rivalité acousmaticiens/mathématiciens

Dès Hippase (vers -450 ?), il semble qu'il y ait eu rivalité entre deux tendances idéologiques (et non plus degrés initiatiques) chez les pythagoriciens : les « Acousmaticiens » et les « Mathématiciens^[38]. » Il ne s'agit plus de la hiérarchie novice/initié, mais de la polarité moraliste/scientifique. D'un côté, les Acousmaticiens insistent sur les paroles (« acousmates ») léguées par Pythagore et privilégient la morale, les prescriptions rituelles, le « mode de vie pythagoricien » ; entre -420 et -350, les auteurs de comédies (Cratinos, Mnésimaque, etc.) décrivent des « pythagoristes », dès Diodore d'Aspendos (vers -380) et Lycon d'Iasos, végétariens et buveurs d'eau, chevelus et barbus, pieds nus, vêtus d'un simple manteau (tribôn), un bâton à la main, faisant vœu de silence et ne se lavant pas. De l'autre côté, les « Mathématiciens » (Hippase, Philolaos, Archytas, Eurytos, Eudoxe de Cnide), au sens de savants, insistent sur les démonstrations et privilégient la science.

Doctrine

De même que le personnage historique de Pythagore est très mal connu, sa pensée s'assimile à l'école pythagoricienne. La pensée de Pythagore lui-même est ainsi recouverte par les apports successifs de ses disciples. La pensée pythagoricienne couvre tous les domaines : "la science relative aux intelligibles et aux dieux ; ensuite la physique ; la philosophie éthique et la logique ; toutes sortes de connaissances en mathématiques et les sciences"^[6]. Archytas, le premier, conçoit ce que sera le quadrivium : arithmétique, musique (arithmétique sensible), géométrie, enfin astronomie (géométrie sensible)^[39]. Pythagore voyait leurs liens : il ramenait les figures de la géométrie aux nombres de l'arithmétique, les sons des musiciens aux proportions des arithméticiens... Des correspondances (ὁμοιὠματα) sont établies, par exemple "le 1 est le point, le 2 la ligne, le 3 le triangle [le plan], le 4 la pyramide [le volume]."^[40]

Arithmétique (et arithmologie)

« Tout est nombre. » Le grand apport de Pythagore, c'est l'importance de la notion de nombre et la naissance d'une mathématique démonstrative (mais aussi religieuse)^[41]. Pour un Grec de l'Antiquité, le nombre désigne toujours un nombre entier et signifie "système arrangé numériquement"(??), "pluralité ordonnée", "chose structurée" ; d'autre part, « un » n'est pas considéré comme un nombre avant Archytas^[42]. Chez les pythagoriciens, les choses sont des nombres, ou les choses consistent en nombres, ou les choses imitent les nombres (qui seraient des principes), ou les choses ont des nombres : un certain flou demeure.

Selon Aristote, pour les pythagoriciens, les choses sont des nombres ; par exemple, un et esprit sont identiques, en musique les intervalles des tons sont des rapports de nombres^[43] ; selon Philolaos de Crotone : les choses ont des nombres, sont faites de nombres ; par exemple, la pyramide contient le nombre 10, le ciel consiste en 10 corps célestes (étoiles, 8 planètes, Anti-Terre)^[44] ; selon Hippase, les choses ont pour modèles les nombres^[45].

La fameuse déclaration « Les choses sont nombre » signifie à la fois : a) c'est le nombre qui constitue la structure intelligible des choses (ce principe fonde en raison la physique mathématique) ; b) les éléments fondamentaux des mathématiques sont les éléments des choses (ce principe affirme la possibilité de définir une structure de l'esprit qui est une structure des choses et que constituent les notions de fini et d'infini, d'un et de multiple, etc.)^[46].

Aristote^[47] : "Les Pythagoriciens s'appliquèrent tout d'abord aux mathématiques... Trouvant que les choses [dont les sons musicaux] modèlent essentiellement leur nature sur tous les nombres et que les nombres sont les premiers principes de la nature entière, les Pythagoriciens conclurent que les éléments des nombres sont aussi les éléments de tout ce qui existe, et ils firent du monde une harmonie et un nombre... Les éléments du nombre sont le pair et l'impair ; et l'un [impair] est fini [limité, structurant, comme une figure géométrique], tandis que l'autre [le pair] est infini [illimité, désordonné, comme l'air]." Il y a "similitude du pair et du féminin, de l'impair et du mâle"^[48]

La Tétraktys

Pythagore donne des nombres une représentation géométrique^[49]. Arithmétique et géométrie sont sœurs. Chaque unité est figurée par un point, de sorte qu'on a des nombres plans (1, 4, 9, 16... sont carrés ; 1, 3, 6, 10... sont triangulaires), rectangulaires, solides (cubiques, pyramidaux...), linéaires, polygonaux. Le premier nombre pyramidal est 4 (selon Philolaos).

Photius : "Ils proclamaient que tout est nombre et que le nombre complet est dix. Le nombre dix, la [décade], est un composé des quatre premiers nombres que nous comptons dans leur ordre. C'est pourquoi ils appelaient Tétraktys [Tétrade] le tout constitué par ce nombre."^[50] 1 + 2 + 3 + 4 = 10 : nombre triangulaire de côté 4, où la tétrade vaut la décade et cache les rapports harmoniques des intervalles de quarte (3:4), quinte (2:3) et octave (1:2)^[6]. Dès Archytas peut-être ou après Platon, les pythagoriciens associent le 1 au point, le 2 à la ligne, le 3 à la surface (la figure géométrique à deux dimensions : cercle, triangle, carré...), le 4 au solide (la figure géométrique à trois dimensions : cube, sphère, pyramide, ect.).

De ces spéculations et de ces graphiques est sortie la table de multiplication^{[réf. nécessaire]}.

"Il a découvert les médiétés" : les proportions, les formules des moyennes^[6] Pythagore découvre 3 des 11 proportions possibles entre 3 termes (a, b, c) : les proportions arithmétique, géométrique et harmonique ; les autres seront découvertes par d'autres pythagoriciens, dont Hippase de Métaponte, Archytas.

• La proportion arithmétique fait que le premier terme dépasse le second de la même quantité que celui-ci dépasse le troisième : a - b = b - c.
• La proportion géométrique (très importante en philosophie et en art) fait que le premier terme est au second ce que le second est au troisième : a/b = b/c.
• La proportion harmonique (essentielle en musique) fait que, "quelle que soit la part de lui-même dont le premier terme dépasse le deuxième, le deuxième dépasse le troisième de la même part de ce troisième" : a = b + a/n. Dans la proportion harmonique 12:8:6, on voit que 8:6 est la quarte, 12:8 la quinte, 12:6 l'octave.

Les pythagoriciens ont pu ainsi résoudre la duplication du carré, la théorisation de la musique, la somme de n termes d'une progression arithmétique, l'extraction des racines carrées^{[réf. nécessaire]}, etc.

La découverte des nombres irrationnels engendra une grave crise. Les pythagoriciens (Hippase de Métaponte) (vers -460) découvrirent l'incommensurabilité de la diagonale et du côté d'un carré, seulement exprimable par racine carrée de deux (√2). [3] Histoire de la racine carrée √2 est un nombre irrationnel. Un nombre irrationnel n'est ni entier ni exprimable par une fraction, or Pythagore pensait en termes de nombres naturels entiers^[51] Chez les Grecs, un n'est pas un nombre, alors racine carrée de 2.^{[réf. nécessaire]}

La science des nombres est à la fois arithmétique, donc scientifique, et arithmologie, donc symbolique. Chaque nombre est un symbole. La justice est quatre, la vie (et le mariage) est cinq^[52], la perfection est dix, etc.^[53]. Philolaos tient que le nombre 1 symbolise le point, le 2 la ligne, le 3 le triangle, le 4 le volume [voir Platon], le 5 les qualités et les couleurs, le 6 l'âme, le 7 l'esprit, la santé et la lumière, 8 l'amour, l'amitié, la ruse et l'intellection, le 10 la perfection^[54].

Musique

Tout commence avec la découverte qu'il existe une relation entre la longueur d'une corde vibrante et la hauteur du son émis. Soit quatre cordes tendues, la première vaut 1, la deuxième a une longueur représentant les 3/4 de la première, la troisième les 2/3 et la dernière la 1/2. Quand on pince successivement ces cordes, on entend le Do, puis la quarte du Do = le Fa, puis la quinte de Do = le Sol, enfin le Do à l'octave. Le son est mathématique.

« Les pythagoriciens affirment que la musique est une combinaison harmonique des contraires, une unification des multiples et un accord des opposés. » (Théon de Smyrne)

Pythagore a découvert les lois de l'harmonique^[55]. Aristote : "Ces philosophes remarquèrent que tous les modes de l'harmonie musicale et les rapports qui la composent se résolvent dans des nombres proportionnels."^[56] La proportion harmonique gouverne les intervalles musicaux. Dans la proportion harmonique 12, 8 et 6, le rapport 12/6 = 2 correspond à l'octave, le rapport 8/6 = 4/3 correspond à la quarte, le rapport 12/8 = 3/2 correspond à la quinte. La gamme pythagoricienne est une gamme musicale construite sur des intervalles de quintes justes, dont le rapport de fréquences vaut 3/2. Les fréquences pythagoriciennes de la note Do sont les suivantes : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048...

Diogène Laërce fait aussi de Pythagore l'inventeur du canon monocorde, un instrument de musique monocorde, appelé "canon". Il illustre la loi selon laquelle "la hauteur du son est inversement proportionnelle à la longueur de la corde".

La musique a une valeur éthique et médicale. "Il faisait commencer l'éducation par la musique, au moyen de certaines mélodies et rythmes, grâce auxquels il produisait des guérisons dans les traits de caractère et les passions des hommes, ramenait l'harmonie entre les facultés de l'âme"^[6].

La musique a une dimension cosmique, comme l'astronomie a une dimension musicale : Platon dira que musique et astronomie sont "sciences soeurs"^[57]. cf l'harmonie des sphères, la musique planétaire^[58]. Pythagore aurait posé que les distances entre les orbites du Soleil, de la Lune et des étoiles fixes correspondent aix proportions réglant les intervalles de l'octave, de la quinte et de la quarte^[59]. Plus tard, « de la voix des sept planètes, de celle de la sphère des [étoiles] fixes » et, en outre, de celle de la sphère au-dessus de nous que l'on appelle 'Anti-Terre', il faisait les neuf Muses."^[5] L'ordre est (pour Pythagore ou les premiers pythagoriciens)^[60] : sphère des étoiles fixes, Saturne, Jupiter, Mars, Soleil, Vénus, Mercure, Lune, Terre, Anti-Terre, Feu central, soit 10 unités. Pythagore retrouve la proportion harmonique où, pour 12 : 8 : 6, on voit que 12:6 est l'octave, 12:8 la quinte, 8:6 la quarte. Si le rayon du Feu central est 1, le rayon de l'orbite de l'Anti-Terre est 3, de la Terre 9, de la Lune 27, de Mercure 81, de Vénus 243, du Soleil 729. Entre la sphère des étoiles fixes et Saturne, entre Saturne et Jupiter, Jupiter et Mars il y a un demi-ton, un ton entre Mars et Soleil, et on obtient une quarte ; entre Soleil et Terre on obtient une quinte, entre étoiles fixes et Terre un octave^[61]. "Pythagore tendait son ouïe et fixait son intellect sur les accords célestes de l'univers. Lui seul, à ce qu'il paraissait, entendait et comprenait l'harmonie et l'unisson universels des sphères [planétaires] et des astres."^[6]

Géométrie

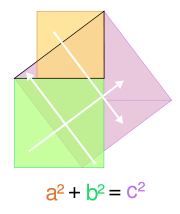Illustration du théorème de Pythagore

Selon Proclos^[62], c'est Pythagore qui le premier étudia la géométrie depuis ses premiers principes afin de lui donner une méthode non empirique purement intellectuelle. C'est là le témoignage le plus précis sur la méthode philosophique de Pythagore. Pythagore, invente la démonstration géométrique, rationnelle, alors qu'elle restait visuelle chez Thalès ou pratiqué de manière empirique chez les Égyptiens et les Babyloniens.

Pythagore est bien connu pour le théorème de géométrie qui porte son nom : le théorème de Pythagore, qui a pour formulation : « dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux côtés de l'angle droit »^[4],[5]. La somme des angles d'un triangle est égale à deux droits (180°), ce qui se démontre facilement pour un triangle rectangle. Cela se prouve de diverses façons : par petits carreaux, par démonstration (Euclide), etc. Pythagore se fonde pour la construction d'angles droits sur le "triangle égyptien", de côtés 3, 4, 5.

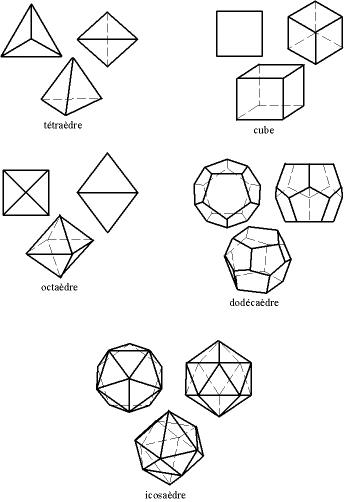
La théorie des solides (ou polyèdres) réguliers et inscriptibles dans une sphère eut une influence considérable. Il n'en existe que 5 : le tétraèdre (la pyramide), le cube, l'octaèdre, le dodécaèdre, et l'icosaèdre^[63]. Pythagore (ou, Hippase de Métaponte, ou, plus vraisemblablement Archytas de Tarente, ne connaissait que le cube, le tétraèdre (la pyramide), et le dodécaèdre. Théétète d'Athènes, mathématicien et médiopythagoricien, découvrit l'octaèdre et l'icosaèdre, en -395 ou en -369.

La solution pour la duplication du cube remonte à Archytas.

Astronomie : le cosmos

Pythagore apporte une connaissance qui émerveille encore le logicien Frege^[64] : l'étoile du soir (celle qu'on voit en premier à la tombée de la nuit) et l'étoile du matin sont une seule et même, c'est Vénus^[65]. Cette identité était connue à Babylone depuis -685.

Pythagore « fut le premier à appeler le ciel cosmos (ordre) et à dire que la Terre est ronde »^[4] ; mais on attribue plus souvent la théorie de la sphéricité de la Terre à Parménide. Les disciples développent l'astronomie pythagoricienne^[66].

Philolaos de Crotone (-470/-fin -V^e s.) affirmerait, le premier, bien avant Copernic, la translation de la Terre autour du Soleil et donc l'héliocentrisme. Philolaos dit : "C'est le Feu qui occupe le milieu."^[67], or ce Feu central n'est pas le Soleil, il reste invisible, on ne perçoit sa lumière que reflétée par le Soleil, c'est une force physique située au milieu du monde. Donc le pythagorisme n'a pas découvert l'héliocentrisme. En revanche, la découverte de la rotation de la Terre sur elle-même revient à un autre pythagoricien, Hicétas de Syracuse (400-335), pour qui « la Terre tourne et pivote sur son axe à très grande vitesse »^[68]. Ecphantos de Syracuse, disciple d'Hicétas (selon August Boekh), dit aussi que "la Terre, centre du monde [géocentrisme], tourne sur elle-même d'Ouest en Est [rotation]". Copernic cite les pythagoriciens :

"D'autres pensent que la Terre se meut. Ainsi, Philolaos le Pythagoricien dit que la Terre se meut autour du Feu en un cercle oblique, de même que le Soleil et la Lune. Héraclide du Pont et Ecphantos le Pythagoricien ne donnent pas, il est vrai, à la Terre un mouvement de translation [mouvement autour du Soleil, héliocentrisme]... Partant de là, j'ai commencé, moi aussi, à penser à la mobilité de la Terre" (Copernic, lettre au pape Paul III, préface à Des révolutions des orbes célestes. De revolutionibus orbium caelestium, 1543).

Aristarque de Samos, astronome aristotélicien, affirmera le premier, vers -280, la rotation de la Terre sur son propre axe et la translation de la Terre autour du Soleil.

L'âme, la transmigration des âmes

Pour Pythagore, le corps (sôma) est un tombeau (sêma), à la fois prison et "signe" ou "protection" de l'âme^[69] : cela est bien une thèse pythagoricienne, pas orphique^[70]. Philolaos : « Les anciens théologiens et devins témoignent eux aussi que c'est en punition de certaines fautes que l'âme a été attelée au corps et ensevelie en lui comme un tombeau. »

L'âme est un nombre, en ce sens qu'elle est harmonie, bonne proportion, combinaison des propriétés composant le corps (c'est la théorie du pythagoricien Simmias dans le Phédon, 86d, de Platon). Elle est vie, car mouvement.

Pythagore pensait "que l'âme est immortelle ; ensuite, qu'elle passe dans d'autres espèces animales ; en outre, qu'à des périodes déterminées ce qui a été renaît, que rien n'est absolument nouveau, qu'il faut reconnaître la même espèce à tous les êtres qui reçoivent la vie. (...) À beaucoup de ceux qui l'abordaient il rappelait la vie antérieure que leur âme avait jadis vécue avant d'être enchaînée à leur corps actuel. Et lui-même, par des preuves irrécusables, démontrait qu'il réincarnait Euphorbe, fils de Panthoos."^[5] L'intervalle entre incarnations serait 216 ans (6 au cube). Et l'explication vient de la nature de l'âme : il y a transmigration de l'âme parce que, par nature, elle est immortelle et mouvante, Pythagore ne fait pas intervenir la justice divine, une rétribution de l'âme, puisque n'importe quelle âme peut entrer dans n'importe quel corps^[71]. D'où vient à Pythagore sa théorie de la transmigration (παλιγγενεσία) des âmes ? d'Orphée ? de Phérécyde de Syros ? depuis l'Inde ? On l'ignore. Pythagore a indiqué ses existences antérieures, dans une liste fixée par Héraclide du Pont^[72] : Aethalide (fils d'Hermès vivant en partie sur terre et en partie dans l'au-delà), Euphorbe (prêtre d'Apollon), Hermotime (chamane), Pyrrhus (simple pêcheur). Il est possible que Pythagore n'ait cru à la réincarnation que pour lui-même.

« Il (Pythagore) racontait sur lui-même les choses suivantes : il avait été autrefois Aithalidès et passait pour le fils d’Hermès ; Hermès lui avait dit de choisir ce qu’il voulait, excepté l’immortalité. Il avait donc demandé de garder, vivant comme mort, le souvenir de ce qui lui arrivait. Ainsi dans sa vie, il se souvenait de tout, et une fois mort il conservait des souvenirs intacts. Plus tard, il entra dans le corps d’Euphorbe et fut blessé par Ménélas. Et Euphorbe disait qu’il avait été Aithalidès [fils d'Hermès], et qu’il tenait d’Hermès ce présent et cette manière qu’avait l’âme de passer d’un lieu à un autre, et il racontait comment elle avait accompli ses parcours, dans quelles plantes et quels animaux elle s’était trouvée présente, et tout ce que son âme avait éprouvé dans l’Hadès, et ce que les autres y supportaient. Euphorbe mort, son âme passa dans Hermotime qui, voulant lui-même donner une preuve, retourna auprès des Branchidées et pénétrant dans le sanctuaire d’Apollon, montra le bouclier que Ménélas y avait consacré (il disait en effet que ce dernier, lorsqu’il avait appareillé de Troie, avait consacré ce bouclier à Apollon), un bouclier qui était dès cette époque décomposé, et dont il ne restait que la face en ivoire. Lorsque Hermotime mourut, il devint Pyrrhos, le pécheur délien ; derechef, il se souvenait de tout, comment il avait été auparavant Aithalidès, puis Euphorbe, puis Hermotime, puis Pyrrhos. Quand Pyrrhos mourut, il devint Pythagore et se souvint de tout ce qui vient d’être dit »

— Diogène Laërce, VIII, 5.

Dans sa théorie de la transmigration des âmes, Pythagore va plus loin que la réincarnation, il admet la métempsycose, c'est-à-dire la croyance que l'âme peut provenir et entrer dans un corps non humain, végétal ou animal. D'où la fameuse anecdote (qui est plutôt une blague venant de Xénophane) :

"Un jour, passant près de quelqu'un qui maltraitait son chien, on raconte qu'il [Pythagore] fut pris de compassion et qu'il adressa à l'individu ces paroles : 'Arrête et ne frappe plus, car c'est l'âme d'un homme qui était mon ami, et je l'ai reconnu en entendant le son de sa voix'" (Diogène Laërce, VIII, 36).

Médecine

Le grand principe biologique n'est ni l'harmonie du semblable par le semblable ni la lutte du contraire par le contraire, mais - comme en musique - l'harmonie des contraires, l'équilibre des puissances dans le corps. De même que l'âme (confondue avec la vie) se définit comme une bonne proportion des propriétés du corps, la santé est la restauration des bonnes proportions entre les propriétés opposées du corps, à savoir l'humide et le sec, le fluide et le visqueux, l'amer et le doux, le pair et l'impair, ect^[73].

En médecine, les pythagoriciens ont leurs techniques : régime, cataplasmes, médicaments, refus des incisions et cautérisations, « incantations pour certaines maladies », musique, « vers choisis d'Homère et d'Hésiode ». On trouve la tripartition indo-européenne : 1) médecine par les herbes relevant des producteurs, 2) médecine par incisions et cautérisations relevant des guerriers, 3) médecine par incantations relevant des roi-prêtres ou philosophes^[6]. Comme la musique purge l'âme, la médecine purge le corps^[74]. La notion de purification, ou de catharsis est centrale^[75].

Alcméon de Crotone, qui semble pythagoricien, pratique la dissection^[76], il place la pensée dans le cerveau, et non plus dans le cœur, comme tous les autres penseurs : « L'hégémonique a son siège dans le cerveau. »^[77]

Science politique (et action)

Pythagore est le fondateur de la science politique. Il défend le régime oligarchique, c'est-à-dire qui confie le gouvernement à une élite, pour lui celle de savants. Il donne un modèle en réduction de l'État dans le fonctionnement de sa communauté^[78]. Il divise la société en trois fonctions sociales - comme tous les Indo-Européens : producteurs, guerriers, rois-prêtres. Il veut organiser la cité de façon mathématique et rationnelle. Il élabore des lois, conservatrices, favorables à la famille, recommandant le respect des lois et des magistrats. Le pythagoricien est militariste, à défendre cette idée : "Il faut combattre, non en paroles, mais en actes, car il est juste et pieux de faire la guerre quand on la fait homme contre homme." La grande idée, c'est qu'il faut remplacer l'égalité démocratique, de type arithmétique (x = y), plébéienne, par une proportionnalité, de type géométrique (A/B=C/D), aristocratique, selon le mérite, et que cette constitution de la société se répandra à l'organisation du monde.

Archytas de Tarente, stratège de Tarente pendant 7 ans mais aussi savant et philosophe pythagoricien, est le type du philosophe-roi. Platon le rencontre physiquement dès -388 et il imagine le philosophe-roi idéal en -370 dans sa République : "Tant que les philosophes ne seront pas rois dans les cités, ou que ceux qu'on appelle aujourd'hui rois et souverains ne seront pas vraiment et sérieusement philosophes... il n'y aura de cesse aux maux des cités" (La République, V, 473 c).

Quelques pythagoriens furent cependant démocrates, dont Théagès^[79].

Enseignements ésotériques

Pythagore dispense des principes exotériques, connus de tous, par exemple : « Il est interdit de prier pour soi-même », « Entre amis, tout est commun »^[4]. Mais d'autres enseignements sont ésotériques, c'est-à-dire réservés aux initiés et d'expression symbolique ; et ils portent sur les secrets de la nature et des dieux. Ces enseignements secrets sont appelés Mémoires (hypomnêmata Ύπομήματα), car il faut s'en souvenir, sans les écrire. Ce sont, d'une part, les "acousmates" (άκούσματα), des dits (prononcés en grec dorien, la langue des pythagoriciens), des préceptes oraux ; ce sont, d'autre part, les "symboles" (σύμβολα), des formules codées, des sommaires (kephalaia κεφάλαια)^[80],[6]. Car « tout ne peut pas être dit à tout le monde. »^[4] "Il y avait chez eux [les pythagoriciens] la règle absolue du silence"^[6].

Jamblique classe les acousmates en trois types, selon qu'ils révèlent l'essence ("qu'est-ce ?"), l'absolu ("qu'est-ce qui est le plus ?") ou le devoir ("que faut-il faire ou pas ?").

• "Qu'est-ce que les Îles des bienheureux ? - Le Soleil et la Lune."
• "Qu'est-ce que l'oracle de Delphes ? - La tétraktys."
• "Qu'est-ce qui est le plus juste ? - Offrir un sacrifice" (de soi, autrement dit "savoir renoncer à quelque chose pour avancer").
• "Qu'y a-t-il de plus savant ? - Le nombre."
• "Ne pas aider à décharger un fardeau. - Il ne faut pas encourager le manque d'effort."
• "Suis dieu (έπου θεώ)"^[6]. C'est la devise du pythagorisme.

En plus des acousmates, préceptes abstraits, il existe une autre catégorie de préceptes, les symboles, qui sont des préceptes pratiques imagés. Les profanes y voient des superstitions ou des bêtises, mais les initiés (μύσται) savent y déchiffrer une idée ou un acte.

• "Ne pas passer par-dessus une balance." Autrement dit : "Pratiquer tous les actes justes", ou "ne pas chercher plus que sa part", et non éviter de façon superstitieuse de "passer au-dessus d'une balance".
• "Ne pas manger le coeur". Éviter la chair crue, ou "ne pas se ronger de chagrin".

En plus, il y a les "symboles secrets" (aporrêta sumbola) ou "signes de reconnaissance" (sunthémata, συνθήματα), qui permettaient aux pythagoriciens initiés de se reconnaître entre eux. Les plus célèbres symboles secrets sont le fameux pentagramme à 5 branches et 5 côtés et la tétraktys.

Le divin Pythagore (...) ne mettait jamais en tête de ses lettres, ni 'Joie' ni 'Prospérité' ; il commençait toujours par Hugiaine ! (υγεία Santé). (...) Voilà pourquoi le triple triangle enlacé, formé de cinq lignes [le pentagramme], qui servait de symbole à tous ceux de cette secte, était nommé par eux 'le signe de la santé'."^[81]

Histoire du pythagorisme

Pièce à l'effigie d'Apollonios de Tyane

Les successeurs (diadoques) de Pythagore à la tête de la communauté pythagoricienne furent : Aristée de Crotone (en -494), son fils Mnésarque ou son fils Telauges, Boulagoras (-380), Gartydas de Crotone, Arésas de Lucanie, Diodore d'Aspendos (-380). Le courant pythagoricien se divise en diverses écoles :

• l'école paléopythagoricienne (pythagorisme ancien, période de ceux qui ont connu Pythagore) : Théanô (épouse de Pythagore), Alcméon de Crotone (-500), Épicharme de Cos (actif vers -480), Hippase de Métaponte (actif vers -460). Les pythagoriciens semblent avoir contrôlé politiquement un territoire allant de Métaponte à Locres jusqu'en -450.
• l'école médiopythagoricienne de Grèce (pythagorisme moyen et récent) : Hippon (-480), Damon le Musicien (-460), Ion de Chios (-450), Polyclète (-420), Philolaos de Crotone (-400) [4], Archytas de Tarente (il rencontra Platon en -388 et -361) [5], Théétète d'Athènes (-395 ou -369), Timée de Locres (contemporain de Platon), Eudoxe de Cnide (-370, il est aussi ami de Platon), Hicétas de Syracuse (vers -360), Ecphantos de Syracuse. Philolaos de Crotone et Archytas de Tarente sont les plus importants. Le pythagorisme au sens strict, né avec Pythagore en -530, rené avec Archytas en -390, disparaît -350.
• l'Ancienne Académie de Platon, pythagorisante : déjà Platon était très pythagorisant dans son Timée (53-56)^[82], encore plus dans son enseignement oral, où il disait les Nombres antérieurs aux Idées. Puis viennent Héraclide du Pont (remplaçant de Platon à l'Académie en -360), Speusippe (scolarque, c'est-à-dire recteur, de l'Académie de Platon en -348), Xénocrate (scolarque en -339). Déjà la distinction pythagorisme/platonisme se brouille. Speusippe remplace les Idées de Platon par les Nombres mathématiques, déduits de deux principes, l'Un et le Multiple. Xénocrate assimile les Idées de Platon aux nombres (selon Aristote, Métaphysique, N, 3) et il tient l'âme pour "un nombre qui se meut de lui-même". Entre les nombres et les choses sensibles (connues par les sens), un pythagoricien ne met pas de coupure, alors qu'un platonicien le fait, il sépare Nombres et choses^[83].
• l'école médiopythagoricienne de Rome : Appius Claudius Caecus (dès -312), Scipion l'Africain (vers -210)^[84], Caton l'Ancien (-209), Ennius (-180). "La plupart des philosophes - académiques, stoïciens, péripatéticiens - pythagorisèrent de quelque façon à Rome"^[85]

L'héritage

Statue de Pythagore à la Cathédrale de Chartres

Influences reçues

Manifestement, le pythagorisme a été influencé par l'orphisme, mais aussi par le chamanisme apollinien des Hyperboréens (Aristéas de Proconnèse, etc.), certainement par la pensée égyptienne, peut-être par les mathématiques et l'astronomie de Babylone.

Influences données

La richesse des travaux entrepris par l'école pythagoricienne a été telle que ses idées et découvertes ont inspiré nombre de courants de pensée. Pythagore a influencé toutes les époques et toutes les cultures d'Occident et d'Orient, toutes les disciplines : mathématiques, musique, philosophie, astronomie... Son encyclopédisme en fait une pensée totale, avec interpénétrations et ramifications.

En art, Pythagore inspire l'architecte romain Vitruve au I^er siècle puis les théoriciens du nombre d'or comme Luca Pacioli illustré par Léonard de Vinci en 1509.

Les écoliers qui étudient le théorème de Pythagore ou apprennent la table de multiplication s'inscrivent dans sa lignée.

Pythagore a fondé une véritable religion, et quantité de légendes. Dans le domaine ésotérique et initiatique, son œuvre continue. Dès 1410, le manuscrit Cooke (ligne 216), un document de base de la franc-maçonnerie opérative, mentionne Hermès et "Pictagoras"^[86]. Des loges franc-maçonniques se réclament de la pensée pythagoricienne, comme la Grande loge suisse alpine (GLSA)^[87], la franc-maçonnerie française ainsi que la Loge italienne.

Bibliographie

Pour une synthèse et une introduction sur Pythagore : J. Mattéi, Pythagore et les Pythagoriens, PUF, coll. «Que-sais-je ?»

Œuvres

Selon la majorité des auteurs, Pythagore n'aurait rien écrit. Porphyre est, à ce sujet, formel : « Car de Pythagore lui-même il n'y avait aucun écrit. »^[5]

Mais ce point est contredit par plusieurs autres notamment Héraclite qui attribue à Pythagore les trois traités suivants : De l'éducation, De la politique et De la nature. Ou encore pour Alexandre Polyhistor, Pythagore aurait laissé uniquement cet ouvrage : Mémoires Pythagoriques. Ces attributions sont fort incertaines, et, dès l'Antiquité, on pensait que ces livres avaient été écrits par des disciples de Pythagore. Et puis, on peut aussi considérer qu'en raison de la coutume persistante de l'ésotérisme chez Pythagore, il n'aurait jamais engager le moindre écrit de ses pensées.

Écrits pythagoriciens

• Traduction de textes pythagoriciens par D. Delattre, Les Présocratiques, édition J.-P. Dumont, Paris, Gallimard, coll. «Bibliothèque de la Pléiade», 1988.
• Lamelles d'or orphico-pythagoriciennes (fin V^e s.-II^e s. av. J.-C.). Orphiques selon William K. Guthrie, pythagoriciennes selon Taylor Thomas, orphico-pythagoriciennes selon Ziegler et Franz Cumont, bacchiques selon Marcel Detienne, éleusiniennes selon Boyancé et Picard. Giovanni Pugliese Caratelli, Les lamelles d'or orphiques. Instructions pour le voyage d'outre-tombe des initiés grec, trad., Les Belles Lettres, 2003, 153 p. [6] Pour Giovanni Pugliese Carratelli (2001), seules sont orphico-pythagoriciennes celles d'Hippanion, Pétélia, Pharsale, Entella, Éleutherna, Mylopotamos.
• Nicomaque de Gérase, Theologoumena arithmeticae (avant 196, date de sa mort), in Photius, Bibliothèque, trad. R. Henry, Paris, Les Belles Lettres, 1959 ; Introduction arithmétique, ed J. Berthier, Paris, Vrin, 1978.
• Diogène Laërce, Vies et doctrines des philosophes illustres (vers 200), livre XIII, trad. sous la direction de M.-O. Goulet-Cazé, Paris, Le Livre de poche, coll. «La Pachotèque», 1999.
• Anatolius, Sur la décade (avant 270), édi. par Heidberg, Annales Internationales d'histoire, Paris, A. Colin, 1901.
• Porphyre, Vie de Pythagore (vers 270), édi. et trad. E. des Places, Paris, Les Belles Lettres, 1982.
• Jamblique, Vie de Pythagore (vers 310), intr., trad. et notes par L. Brisson et A. Ph. Segonds, Paris, Les Belles Lettres, 1996.
• Pseudo-Lysis, Les vers d'or (IV^e s. ?)
• Hiéroclès, Commentaire sur les vers d'or des pythagoriciens (vers 480 ?), trad. Mario Meunier, Paris, L'artisan du livre, 1930.

Études antiques

• Aristote, Des Pythagoriciens (Περί των Πυθαγορείων) (vers 360 av. J.-C. ?), trad. an. : The Complete Works of Aristotle, J. Barnes édi., Princeton University Press, 1984, p. 2441-2446.
• Speusippe, Sur les nombres pythagoriciens (vers 350 av. J.-C. ?), trad. Tannery, Pour l'histoire de la science hellène, Paris 1887.
• Théon de Smyrne, Exposition des connaissances mathématiques utiles pour la lecture de Platon (vers 130 ?), trad. J. Dupuis, Paris, Hachette, 1892.

Études modernes

• Boyancé P.., Les Muses et l'harmonie des sphères, Paris, 1946.
• Caveing M., La figure et le Nombre. Recherches sur les premières mathématiques des Grecs, Lille, 1997.
• Chaignet A. E., Pythagore et la philosophie pythagoricienne, 2 t., Paris, Didier, 1874. Le volume 2 contient : "Exposition de la doctrine philosophique", p. 1-213. "Histoire [de l'école pythagoricienne", p. 215-349. "Critique", p. 351-379. [7]
• Armand Delatte, Études sur la littérature pythagoricienne, Paris, Champion, 1915, 314 p.
• Armand Delatte, Essai sur la politique pythagoricienne, Paris, Champion, 1922, 295 p. Rééd. Genève, Slatkine, 1979.
• Armand Delatte, La vie de Pythagore de Diogène Laërce, Bruxelles, 1922[8]
• Ghyka M., Le nombre d'or, 2 vol. Paris. Gallimard, 1931, réed. Paris, Gallimard, 1977.
• Gobry I., Pythagore, Paris, Seghers, 1973.
• Hamelin O., Les philosophes présocratiques, Strasbourg, Université de Strasbourg, 1978.
• Jean Mallinger, Pythagore et les Mystères, Paris, Niclaus, 1944 ; 2^e éd. revue et corrigée, Lille, F. Planquart, 1974.
• Mario Meunier, Les vers d'or, Guy Trédaniel, édition de la Maisnie, 1987.
• Gaston Milhaud, Les philosophes géomètres de la Grèce. Platon et ses prédécesseurs (1900), Vrin, 1934.
• André Pichot, La naissance de la science, t. 2 : Grèce antique, Gallimard, coll. "Folios Essais", 1991, p. 127-238. Lumineux.
• Louis Rougier, La religion astrale des Pythagoriciens, Paris, PUF, 1959, 122 p.
• Eduard Zeller, La philosophie des Grecs dans son développement historique (1844-1868, 2° éd. 1 856 t. I p. 361-617), I, 1, trad. de l'all. É. Boutroux, 1877, t. I, p. 280-474 [9]

Notes et références

Voir aussi

Articles connexes

• Théorème de Pythagore
• École pythagoricienne
• Jamblique
• Néopythagorisme
• Philolaos
• Table de multiplication

Liens externes

• Répertoires de ressources philosophiques antiques :

• Bibliotheca Classica Selecta
• Cnrs
• Remacle
• Site Académique Toulouse

• Portail de la Grèce antique
• Portail de la philosophie antique
• Portail des mathématiques
• Portail de l’astronomie