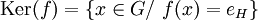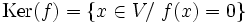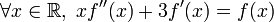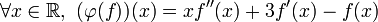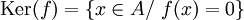Noyau d'un homomorphisme

En mathématiques et plus particulièrement en algèbre générale, le noyau d'un morphisme mesure le degré auquel un morphisme n'est pas injectif.

Dans de nombreux cas, le noyau d'un morphisme est un sous-ensemble de l'ensemble de définition du morphisme (plus particulièrement, l'ensemble des éléments qui sont envoyés sur l'élément neutre de l'ensemble d'arrivée). Dans des contextes plus généraux, le noyau est à la place interprété comme une relation d'équivalence sur l'ensemble de définition (plus particulièrement, la relation qui relie les éléments qui sont envoyés sur une même image par le morphisme).

Dans l'une ou l'autre de ces situations, le noyau est trivial si et seulement si le morphisme est injectif ; dans la première situation « trivial » signifie constitué uniquement de l'élément neutre, tandis que dans le second, cela signifie que la relation est l'égalité.

Le noyau d'un morphisme f est noté souvent Ker(f), qui vient de Kernel, mot anglais pour désigner le noyau d'un morphisme.

Dans cet article, nous examinons diverses définitions du noyau, utilisées pour les types importants de morphismes.

Sommaire 1 Noyau d'un morphisme de groupe 2 Noyau d'une application linéaire 3 Noyau d'un morphisme d'anneau 4 Noyau d'un morphisme de corps 5 Noyau en général 6 Articles connexes

Noyau d'un morphisme de groupe

Le noyau d'un morphisme de groupes f d'un groupe G vers un groupe H se compose de tous les éléments de G qui sont envoyés par f sur l'élément neutre e_H de H. Formellement :

Le noyau est un sous-groupe distingué de G.

L'un des théorèmes d'isomorphisme énonce que le groupe quotient G / Ker(f) est isomorphe à l'image de f, par l'isomorphisme induit par f lui-même.

Une proposition légèrement plus générale est le théorème fondamental des morphismes.

Le morphisme de groupe f est injectif si et seulement si le noyau de f n'est constitué que de l'élément neutre de G.

Noyau d'une application linéaire

Si f est une application linéaire d'un espace vectoriel V dans un espace vectoriel W, alors le noyau de f est défini par

Le noyau est un sous-espace de l'espace vectoriel V, et l'espace quotient V / Ker(f) est isomorphe à l'image de f; en particulier, nous avons pour les dimensions :

dimKer(f) = dimV − dimIm(f)

L'application linéaire f est injective si et seulement si Ker(f) = {0}.

Si V et W sont des espaces vectoriels de dimension finie sur un corps , de dimension respective n et p et que des bases de ces espaces sont données, alors f peut être représentée par une matrice 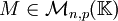, et le noyau peut être déterminé en résolvant le système homogène d'équations linéaires MX = 0.

Dans cette représentation, les solutions de ce système correspondent aux coordonnées des vecteurs du noyau de f ; mais aussi aux vecteurs du noyau de l'application linéaire canoniquement associée à la matrice M.

La dimension du noyau, est donnée par le nombres de colonnes de M moins le rang de M.

Résoudre des équations différentielles homogènes nous mène souvent à la détermination du noyau d'une certaine application linéaire.

Par exemple, si nous désirons déterminer les fonctions deux fois dérivables f de dans telles que

nous avons à considérer le noyau de l'application linéaire 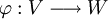, où V est l'espace vectoriel de toutes les fonctions deux fois dérivables de dans , W est l'espace vectoriel de toutes les fonctions de dans , et pour 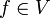, nous définissons 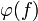par la condition

Noyau d'un morphisme d'anneau

Le noyau d'un morphisme d'anneau f d'un anneau A dans un anneau B se compose de tous les éléments x de A pour lequel f(x) = 0. Formellement cela nous donne

Un tel noyau est toujours un idéal bilatère de A. Le théorème d'isomorphisme mentionné ci-dessus pour des groupes et des espaces vectoriels reste valable dans le cas des anneaux.

Noyau d'un morphisme de corps

Le noyau d'un morphisme de corps (c'est-à-dire un morphisme d'anneau où les anneaux considérés sont des corps) est toujours réduit à l'élément neutre 0, de sorte que tout morphisme de corps est injectif.

Noyau en général

Toutes ces notions de noyaux se généralisent dans le cadre de la théorie des catégories abéliennes.

Articles connexes

• Lemme des noyaux
• catégorie abélienne

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

• Portail des mathématiques