- Isomorphe
-
Isomorphisme
 Pour l'isomorphisme en chimie, voir Isomorphisme (chimie).
Pour l'isomorphisme en chimie, voir Isomorphisme (chimie). Pour l'isomorphisme institutionnel, voir Isomorphisme institutionnel.
Pour l'isomorphisme institutionnel, voir Isomorphisme institutionnel.En mathématiques, un isomorphisme est une relation entre deux objets qui démontre leurs similitudes. Par exemple, en théorie des groupes, il permet de déduire plusieurs propriétés d'un groupe à partir d'un autre.
Sommaire
Définitions
Algèbre
En algèbre, un isomorphisme est un morphisme admettant un inverse qui est lui-même un morphisme.
C'est donc une bijection pour laquelle les relations « algébriques » entre les éléments de l'ensemble d'arrivée sont les mêmes que celles entre leurs antécédents respectifs (la structure algébrique est préservée). Ce « méta-concept » mathématique admet une définition formelle en théorie des catégories.
Catégorie
En théorie des catégories, un isomorphisme est un morphisme
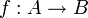 d'une catégorie C qui possède
d'une catégorie C qui possède- un inverse à gauche : il existe un morphisme
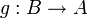 tel que
tel que 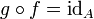 ,
, - et un inverse à droite : il existe un morphisme
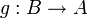 tel que
tel que 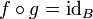 .
.
Remarquons qu'avec une notation covariante telle que « ; » à la place de la notation contravariante « ∘» pour la composition des morphismes, il faudrait inverser ces deux dernières définitions, ou alors préférer appeler ces inverses respectivement post-inverse et pré-inverse.
L'existence d'un inverse à gauche n'entraîne pas l'existence d'un inverse à droite, et réciproquement. C'est par exemple le cas dans la catégorie des ensembles.
Exemples
- Dans la catégorie des espaces topologiques, un isomorphisme est une bijection continue d'inverse continue, aussi appelée homéomorphisme.
- De la même façon, un isomorphisme entre variétés différentielles (par exemple, entre des ouverts de
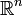 ) est un difféomorphisme. Plus précisément, si l'on considère une structure
) est un difféomorphisme. Plus précisément, si l'on considère une structure 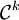 sur une variété, alors on parle de
sur une variété, alors on parle de 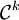 -difféomorphisme.
-difféomorphisme.
Propriétés
Un isomorphisme est à la fois un épimorphisme et un monomorphisme, mais la réciproque est fausse en général : il existe des morphismes à la fois épiques et moniques qui ne sont pas des isomorphismes.
Pour plus de détails, voir : Propriétés des morphismes dans les catégories.
Objets isomorphes
Deux objets reliés par un isomorphisme sont dits isomorphes.
Selon certains points de vues, deux objets isomorphes peuvent être considérés comme identiques, ou du moins indistinguables. En effet, bien souvent, les propriétés intéressantes d'un objet seront partagées par tous les objets isomorphes de la catégorie. Ainsi on parle souvent d'unicité ou d'identité « à un isomorphisme près ».
Exemple
On dira souvent qu'il n'y a qu'un seul
 -espace vectoriel de dimension n (« à un isomorphisme près »). Cela est vrai au sens où toutes les propriétés d'espace vectoriel (relatives à la catégorie des espaces vectoriels) démontrées sur
-espace vectoriel de dimension n (« à un isomorphisme près »). Cela est vrai au sens où toutes les propriétés d'espace vectoriel (relatives à la catégorie des espaces vectoriels) démontrées sur 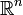 se vérifieront de la même manière, par exemple, sur
se vérifieront de la même manière, par exemple, sur ![\R[X]/(X^{n})](/pictures/frwiki/98/b1c7608716fcac445cab785d57ed0b4e.png) (anneau des polynômes formels quotienté par l'idéal engendré par Xn). En revanche, si l'on considère
(anneau des polynômes formels quotienté par l'idéal engendré par Xn). En revanche, si l'on considère ![\R[X]/(X^{n})](/pictures/frwiki/98/b1c7608716fcac445cab785d57ed0b4e.png) en tant qu'anneau (c’est-à-dire dans la catégorie des anneaux), cela n'a plus aucun sens. L'anneau
en tant qu'anneau (c’est-à-dire dans la catégorie des anneaux), cela n'a plus aucun sens. L'anneau ![\R[X]/(X^{n})](/pictures/frwiki/98/b1c7608716fcac445cab785d57ed0b4e.png) a en effet de nombreuses propriétés en tant qu'anneau qu'on ne peut transposer à
a en effet de nombreuses propriétés en tant qu'anneau qu'on ne peut transposer à 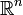 qui n'en est pas un.
qui n'en est pas un.Cette identification entre deux objets n'a lieu que dans une catégorie bien précise, où il existe un isomorphisme entre ces deux objets.
Liens internes
- Portail des mathématiques
Catégories : Algèbre générale | Théorie des catégories - un inverse à gauche : il existe un morphisme
Wikimedia Foundation. 2010.
