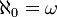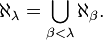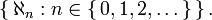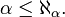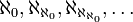Aleph (Nombre)

En théorie des ensembles, les alephs sont les cardinaux des ensembles infinis bien ordonnés. En quelque sorte le cardinal d'un ensemble représente sa « taille », indépendamment de toute structure que puisse avoir cet ensemble (celle d'ordre en particulier dans le cas présent). Ils sont nommés ainsi d'après la lettre aleph, notée א, première lettre de l'alphabet hébreu, qui est utilisée pour les représenter. En effet on montre que les alephs forment une classe propre elle même « bien ordonnée », et il existe alors une et une seule « bijection » (une classe fonctionnelle bijective) croissante de la classe des ordinaux dans la classe des alephs. On utilise la notation ℵ_α pour désigner l'image de α par cette « bijection ».

En présence de l'axiome du choix les alephs représentent les cardinaux de tous les ensembles infinis, en vertu du théorème de Zermelo qui dit qu'alors tout ensemble peut être bien ordonné. La définition même des alephs n'utilise cependant pas l'axiome du choix.

Le plus petit aleph est le cardinal des entiers naturels, et on le note donc aleph-zéro ℵ₀. Le suivant est noté aleph-un, ℵ₁, puis ℵ₂, et ainsi de suite.

La notation a été introduite par Georg Cantor, qui le premier s'est intéressé à la relation d'équipotence entre ensembles infinis, le fait d'être en bijection, et a réalisé que deux ensembles infinis pouvaient ne pas être équipotents. Il a ensuite introduit la notion de nombre cardinal, un nombre qui caractérise une classe d'équivalence pour l'équipotence. Pour Cantor, qui utilise implicitement l'axiome du choix, ou plutôt plus directement que tout ensemble peut être bien ordonné, les alephs représentent tous les cardinaux infinis.

Sommaire 1 Définition 2 Ordinal de Hartogs 3 Aleph-zéro 4 Aleph-un 5 Continu 6 Aleph-ω 7 Points fixes 8 Voir aussi 8.1 Liens internes 8.2 Liens externes

Définition

Plus formellement, dans la théorie des ensembles de Zermelo-Fraenkel, on appelle ordinal initial un ordinal qui n'est équipotent à aucun ordinal strictement inférieur, on dit simplement cardinal en présence de l'axiome du choix. Un ordinal étant par définition bien ordonné, tout ordinal est donc équipotent à un ordinal initial, et par la même tout ensemble bien ordonné également. Tout ordinal fini est un ordinal initial. Un aleph est par définition un ordinal initial infini. Le plus petit ordinal infini, ω, qui correspond au bon ordre sur les entiers naturels, est également le plus petit aleph, et on le note, en tant que cardinal, ℵ₀.

La classe des ordinaux est une classe propre : c'est une version positive du paradoxe de Burali-Forti. On en déduit, grâce au schéma d'axiomes de remplacement que la classe des ordinaux initiaux est aussi une classe propre.

En effet, si ce n'était pas le cas, à partir d'un certain rang les ordinaux seraient tous équipotents, soit α le plus petit d'entre eux. Tout ordinal serait alors subpotent à α, et donc isomorphe à un bon ordre sur une partie de α. Un tel bon ordre est défini par son graphe : une partie de α × α. On peut donc définir par compréhension sur l'ensemble des parties de α × α, l'ensemble des bons ordres définis sur une partie de α. On associe à chacun de ces bons ordres son ordinal, et les ordinaux ainsi obtenus forment un ensemble par remplacement, ce ne peut donc être la classe de tous les ordinaux d'où la contradiction.

La classe des alephs est donc elle-même une classe propre, puisque les ordinaux initiaux finis forment un ensemble (qui est celui des entiers naturels).

Une classe propre d'ordinaux est forcément image de la classe des ordinaux par une unique classe fonctionnelle bijective croissante : définition par induction ordinale pour l'existence, démonstration par induction ordinale pour l'unicité. Pour expliciter la définition, on va noter ρ → ρ⁺ le successeur sur les ordinaux initiaux (c'est le successeur cardinal, qui diffère du successeur ordinal) : à ρ il associe le plus petit des ordinaux strictement supérieur à ρ et non équipotent à ρ, sachant qu'il existe forcément un tel ordinal, puisque la classe des ordinaux initiaux est une classe propre, et que toute classe non vide d'ordinaux a un plus petit élément.

Il est possible alors de définir la suite ordinale aleph de la façon suivante :

et pour λ, un ordinal limite infini :

Cette définition n'a pas nécessité l'axiome du choix. Cependant en l'absence de celui-ci, on ne peut vraiment dire que ℵ₀ est le plus petit cardinal infini : il pourrait exister des ensembles qui sont infinis, c'est-à-dire équipotents à aucun entier, mais ne contiennent pas de partie dénombrable. De façon analogue, sans l'axiome du choix, tout ce que l'on peut dire du successeur cardinal ρ⁺ de ρ, c'est que tout ensemble qui aurait un cardinal compris entre ρ et ρ⁺, au sens de la subpotence, serait soit ρ soit ρ⁺. En effet un ensemble qui s'injecte dans l'ordinal ρ⁺ est nécessairement bien ordonné. Donc ρ⁺ est bien minimal, parmi les ensemble ayant un cardinal supérieur à ρ au sens de la subpotence, c'est-à-dire les ensembles dans lesquels ρ s'injecte. Par contre, sans axiome du choix, rien ne permet de dire qu'il en est le plus petit élément.

Il est possible de donner une définition plus explicite du successeur cardinal. C'est l'objet de la section qui suit.

Ordinal de Hartogs

Il est possible d'associer à tout ensemble un ordinal initial, que l'on appelle ordinal ou cardinal de Hartogs, de la façon suivante. L'ordinal de Hartogs d'un ensemble a est l'ensemble de tous les ordinaux subpotents à a. Cet ensemble est évidemment un segment initial de la classe des ordinaux, donc un ordinal. Il est également évidemment initial.

Quand a est un ordinal initial ρ, l'ordinal de Hartogs de ρ n'est autre que ρ⁺, le successeur cardinal de ρ.

Aleph-zéro

Aleph-zéro (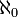) est par définition le cardinal de l'ensemble des entiers naturels. Si l'axiome du choix est vérifié, il s'agit également du plus petit cardinal infini. Un ensemble a 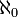pour cardinal si et seulement s'il est infini et dénombrable.

Aleph-un

Aleph-un (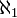) est le cardinal de l'ensemble des nombres ordinaux dénombrables (un ensemble lui-même non dénombrable). Si l'axiome du choix est utilisé, 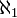est le plus petit cardinal qui suit .

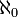Continu

Le cardinal de l'ensemble des nombres réels est 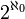. Dans le cadre de la théorie des ensembles de Zermelo-Fraenkel munie de l'axiome du choix, l'hypothèse du continu est l'affirmation que  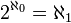; en l'absence de cette hypothèse, la place de 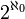dans la hiérarchie des aleph n'est pas définie avec certitude, et on peut même démontrer que 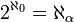est compatible avec ZFC pour la plupart des valeurs de α > 0 (mais pas pour α de cofinalité ω, par exemple)

Aleph-ω

Conventionnellement, le plus petit ordinal infini est noté ω et le cardinal 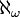est la borne supérieure de

Points fixes

Pour tout ordinal α :

Dans beaucoup de cas, 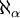est strictement supérieur à α. Certains ordinaux limites sont des points fixes de la fonction aleph. Le premier cardinal de ce type est la limite de la suite

Tout cardinal inaccessible est également un point fixe de la fonction aleph.

Voir aussi

Notion de nombre
Ensembles usuels	Entier naturel • Entier relatif • Nombre décimal • Nombre rationnel • Nombre réel • Nombre complexe
Extensions	Quaternion • Octonion • Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

Liens internes

• Beth (nombre)
• Georg Cantor
• Ensemble dénombrable
• Ensemble infini
• Hypothèse du continu
• Nombre cardinal
• Nombre transfini

Liens externes

• (en) Aleph-0 (MathWorld)
• (en) Aleph numbers (PlanetMath)

• Portail des mathématiques