Hypothese du continu

En théorie des ensembles, l'hypothèse du continu, due à Georg Cantor, affirme qu'il n'existe aucun ensemble dont le cardinal est strictement compris entre le cardinal de l'ensemble des entiers naturels et celui de l'ensemble des nombres réels. En d'autres termes : tout ensemble strictement plus grand, au sens de la cardinalité, que l'ensemble des entiers naturels doit contenir une « copie » de l'ensemble des nombres réels. Cantor avait démontré (et publié en 1874) que le cardinal de l'ensemble des nombres réels était strictement plus grand que celui des nombres entiers, il formula plus tard cette hypothèse, qui résultait d'une analyse des sous-ensembles de la droite réelle, et de sa hiérarchisation des cardinaux infinis, mais il tenta en vain de la démontrer. Cette démonstration constituait le premier de la célèbre liste des 23 problèmes de Hilbert, que celui-ci avait établie pour le congrès international de mathématiques de 1900 à Paris, afin de guider la recherche en mathématiques du siècle alors naissant.

Ce n'est que bien plus tard, en 1963, que Paul Cohen introduisit sa méthode de forcing pour montrer que cette hypothèse ne pouvait se déduire des axiomes de la théorie des ensembles ZFC, généralement considérée comme une formalisation adéquate de la théorie des ensembles de Cantor, qui n'était pas encore axiomatisée en 1900. Kurt Gödel avait précédemment démontré, en 1938, que cette hypothèse n'était pas non plus réfutable dans ZFC^[1]. Elle est donc indépendante des axiomes de la théorie des ensembles ZFC, ou encore indécidable dans cette théorie.

La méthode du forcing de Cohen a connu depuis de nombreux développements en théorie des ensembles. Son résultat n'a pas mis un point final aux travaux sur le sujet. La recherche d'hypothèses naturelles à ajouter à la théorie ZFC et d'arguments qui permettraient de trancher pour ou contre l'hypothèse du continu constitue toujours un sujet actif en théorie des ensembles.

Sommaire 1 Définition de l'hypothèse du continu 2 Cardinalité 3 Indécidabilité 4 Généralisation 5 Hypothèse généralisée du continu et axiome du choix 6 Possible réfutation de l’hypothèse du continu 7 Notes 8 Bibliographie

Définition de l'hypothèse du continu

On définit 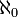(aleph zéro) comme le cardinal de . Le cardinal de est noté usuellement .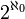
Soit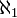 le plus petit cardinal strictement supérieur à 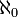, l'hypothèse du continu déclare que 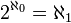. En d'autres termes, cela signifie qu'il n'existe pas d'ensemble infini dont le cardinal serait strictement compris entre le cardinal de et celui de . On passe donc du dénombrable (ou discret), au continu, en faisant un seul bond.

Cardinalité

Deux ensembles S et T sont équipotents, ou encore ont même cardinalité, lorsqu'il existe une bijection entre S et T. Cela signifie que l'on peut associer à chaque élément de S un unique élément de T et réciproquement. Cette notion de cardinalité, un peu informelle car le cardinal d'un ensemble n'a pas été véritablement défini, suffit pour bien des aspects élémentaires. La définition d'un cardinal en tant qu'ensemble, plus précisément d'ordinal, due également à Cantor, nécessite l'axiome du choix.

Avec des ensembles infinis, certaines analogies peuvent tromper. Naïvement, il semble y avoir plus de nombres rationnels que de nombres entiers : un rationnel est le quotient de deux entiers. Cependant, cette vision est erronée, car il est possible d'énumérer tous les rationnels en les indexant par les entiers naturels, c'est-à-dire d'établir une bijection entre ces deux ensembles. Un tel ensemble, équipotent à l'ensemble des entiers naturels, est dit infini dénombrable ou parfois simplement dénombrable.

L'ensemble des nombres réels, noté , est un exemple d'ensemble non-dénombrable. Cantor en a proposé en 1891 une seconde démonstration très simple utilisant l'argument de la diagonale. Le continu désigne la droite réelle d'où le nom de l'hypothèse.

On peut reformuler ainsi l'hypothèse du continu : tout sous-ensemble du continu est soit fini, soit infini dénombrable, soit a la même cardinalité que le continu.

Indécidabilité

Kurt Gödel a montré en 1938 que l'ajout de l'hypothèse du continu à la théorie des ensembles, définie par exemple par les axiomes de Zermelo-Fraenkel, ne changeait nullement la consistance de cette théorie, même si on l'augmente de l'axiome du choix.

Paul Cohen a montré en 1963 que l'hypothèse du continu n'était pas démontrable dans la théorie des ensembles basée sur les axiomes de Zermelo-Fraenkel. Elle est donc indépendante de la théorie des ensembles.

Commencée il y a une trentaine d'années, la recherche d'axiomes « naturels » à ajouter à la théorie de Zermelo-Fraenkel (axiomes de détermination, axiomes de grands cardinaux, etc.) va sans doute permettre, grâce aux travaux de W. Hugh Woodin, de résoudre prochainement l'hypothèse du continu... par la négative (voir ci-dessous), ce que soupçonnait déjà Gödel^[2].

Il n'y a pas de quoi être surpris de l'existence d'énoncés ne pouvant être démontrés ou infirmés à partir d'un système d'axiomes donné, c'est par exemple le cas du postulat d'Euclide relativement à son système « axiomatique ».

L'hypothèse du continu n'est pas sans rapport avec des énoncés d'analyse, ou de théorie de la mesure.

Historiquement, les mathématiciens en faveur d'une large classe d'ensembles rejettent l'hypothèse du continu, alors que ceux favorables au contraire à une ontologie ensembliste plus restreinte l'acceptent.

Généralisation

L'hypothèse généralisée du continu dit qu'il n'existe pas d'ensemble dont le cardinal serait strictement compris entre 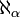et 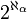, α parcourant les ordinaux et 2^κ étant le cardinal de l'ensemble des parties d'un ensemble de cardinal κ.

On aurait alors 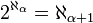 : il n'y aurait rien entre un cardinal et l'ensemble de ses parties, à bijection près. Cette hypothèse, plus forte que celle du continu, est également indécidable d'après les travaux de Gödel et Cohen.

Hypothèse généralisée du continu et axiome du choix

Pour définir la notion de nombre cardinal d'un ensemble dans la théorie ZFC on a besoin de l'axiome du choix. Un cardinal est un ordinal qui n'est pas équipotent à un ordinal strictement plus petit (c'est-à-dire en bijection avec celui-ci), et on peut associer à tout ensemble un ordinal en utilisant le théorème de Zermelo (équivalent à l'axiome du choix). Si on se contente d'une notion plus informelle de cardinal — une classe d'équivalence pour la relation d'équipotence (une telle classe ne peut être un ensemble), il faut prendre garde, qu'en l'absence de l'axiome du choix, deux classes ne sont pas nécessairement comparables. Plus précisément on dit que a est subpotent à b quand il existe une injection de a dans b, strictement subpotent quand de plus il n'y a pas de bijection entre a et b. La « totalité » de l'ordre ainsi défini (voir théorème de Cantor-Bernstein) entre cardinaux, est historiquement appelée propriété de trichotomie des cardinaux, car elle peut s'énoncer ainsi : étant donné deux ensembles a et b, soit a est strictement subpotent à b, soit b est strictement subpotent à a, soit a et b sont équipotents. La propriété de trichotomie des cardinaux est équivalente à l'axiome du choix dans ZF.

On peut cependant énoncer de façon naturelle l'hypothèse du continu généralisée dans la théorie ZF

Pour tout ensemble infini a, tout ensemble b qui est subpotent à l'ensemble des parties de a et tel que a soit subpotent à b, est équipotent soit à a soit à son ensemble des parties.

Cet énoncé est bien équivalent aux énoncés précédents de l'hypothèse généralisée du continu, en présence de l'axiome du choix.

On peut donc se poser la question dans la théorie ZF du rapport entre l'hypothèse du continu généralisée et l'axiome du choix. Wacław Sierpiński a montré en 1947^[3] que l'hypothèse généralisée du continu a pour conséquence l'axiome du choix dans la théorie ZF.

Par contre la théorie ZF seule n'implique pas l'axiome du choix, comme l'a montré Paul Cohen dans le même article que celui sur l'indépendance de l'hypothèse du continu, en utilisant sa méthode de forcing, combinée avec la méthode de permutation développée par Adolf Fraenkel et Andrzej Mostowski (qui avaient déjà obtenus des résultats dans cette direction).

Possible réfutation de l’hypothèse du continu

Des travaux récents de W. Hugh Woodin laissent entendre que l'hypothèse du continu est essentiellement fausse^{[Quoi ?]}. L'auteur a introduit une méta-logique appelée Ω-logique basée sur les ensembles projectifs. La Ω-conjecture de Woodin dit que tout énoncé essentiellement vrai dans la Ω-logique est Ω-prouvable. De sérieux indices laissent à penser que ce postulat est vrai. En utilisant des axiomes de grands cardinaux plus la conjecture ci-dessus, on en déduit que l'hypothèse du continu est essentiellement fausse.^[4]

Notes

Bibliographie

• Kurt Gödel, The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory, 1940, Princeton University Press.
• Kurt Gödel, What is Cantor's continuum problem?, 1947, The American Mathematical Monthly 54 : 515-25. Version révisée in Paul Benacerraf et Hilary Putnam, eds., 1984 (1964). Philosophy of Mathematics : Selected Readings, Cambridge Univ. Press: 470-85. Article informel de réflexion sur l'hypothèse du continu.
• Paul Cohen, Set Theory and the Continuum Hypothesis, W. A. Benjamin.
• Paul Cohen, The Independence of the Continuum Hypothesis, Proceedings of the National Academy of Sciences of the United States of America 50 (6): 1143–1148, 15 décembre 1963.
• Paul Cohen, The Independence of the Continuum Hypothesis, II, Proceedings of the National Academy of Sciences of the United States of America 51 (1): 105–110, 15 janvier 1964.

Problèmes de Hilbert

Premier problème - Deuxième problème - Troisième problème - Quatrième problème - Cinquième problème - Sixième problème - Septième problème - Huitième problème - Neuvième problème - Dixième problème - Onzième problème - Douzième problème - Treizième problème - Quatorzième problème - Quinzième problème - Seizième problème - Dix-septième problème - Dix-huitième problème - Dix-neuvième problème - Vingtième problème - Vingt-et-unième problème - Vingt-deuxième problème - Vingt-troisième problème

• Portail des mathématiques