Equation (mathematiques elementaires)

Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Logique

Arithmétique

Probabilités

Statistiques

Une équation est une question, une égalité entre deux quantités algébriques. Cette égalité contient des inconnues. Résoudre l'équation, c'est trouver les valeurs des inconnues qui rendent vraie l'égalité.

En voici des exemples :

• 3x + 5 = 15, on cherche x
• 2y − 3 = 7, on cherche y
• z² − 2z + 1 = 0 , on cherche z
• etc.

Inconnue

L'inconnue (ou les inconnues s'il y en a plusieurs) peuvent s'appeler comme on le souhaite, il est préférable de choisir un nom usuel et facile à retenir au vu de la chose désignée, par exemple :

• Appeler c le côté d'un carré
• Appeler p le poids d'un objet, F une force
• Appeler n un nombre entier quelconque

Les inconnues peuvent être des fonctions ou tout autre objet mathématique :

• Une équation fonctionnelle est une équation dont l'inconnue est une fonction ; par exemple, trouver les fonctions f vérifiant pour tout a et b réels
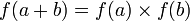
• Une équation différentielle contient des dérivées, comme trouver les fonctions vérifiant pour tout x réel f'(x) = 2f(x) + sin(x)

L'ensemble des nombres utilisés n'est pas nécessairement ℝ, il peut être étendu à ℂ ou limité à ℕ, voire concerner des objets non numériques comme des transformations du plan ou des objets algébriques abstraits.

Résolution des équations

Les équations se résolvent en respectant quelques règles de bon sens, qu'on peut interpréter comme déjà données par Euclide dans ses Éléments, les notions communes. Note : il s'agit d'une interprétation car Euclide ne traite pas d'équation (elles lui sont postérieures), il s'agit d'une application de ces notions communes aux équations modernes. D'ailleurs les deux dernières mises en italiques ne sont pas dans ses Éléments, elles sont ici parce qu'elles sont dans le même style que les autres.

1. Les grandeurs égales à une même grandeur, sont égales entr'elles.

   Donc si a=b et si b=c alors a=c, c'est la transitivité de l'égalité

2. Si à des grandeurs égales, on ajoute des grandeurs égales, les touts seront égaux.

   Ce qui veut dire qu'on a le droit d'ajouter des quantités égales de chaque côté d'une égalité

3. Si à des grandeurs égales, on retranche des grandeurs égales, les restes seront égaux.

   C'est la même chose que ci-dessus mais pour la soustraction

4. Si à des grandeurs égales, on multiplie des grandeurs égales, les produits seront égaux.

   Il faut prendre garde à ne pas multiplier par zéro sous peine de vite écrire des égalités sans intérêt

5. Si à des grandeurs égales, on divise des grandeurs égales, les quotients seront égaux.

   Il faut prendre garde à ne pas diviser par zéro, et donc étudier les valeurs du quotient en conséquence

En fait, ces transformations sont des fonctions qui ne changent pas les solutions de l'équation. En d'autres termes, les solutions de l'équation initiale et celles de l'équation après utilisation d'une notion commune sont les mêmes. Ce n'est pas le cas de toutes les fonctions, la fonction carré en est le premier exemple rencontré.

Enfin, toutes les manipulations algébriques ou numériques habituelles sont autorisées dans chacun des membres de l'équation (factorisation, développement, réduction...).

Les premières méthodes de résolution d'équations utilisent des raisonnements géométriques issus essentiellement des résultats simples de la géométrie du triangle et du carré. Ces méthodes sont développées dans l'article algèbre géométrique.

Résolution d'équations particulières

• Une équation du premier degré est une équation qui se ramène à une équation du type ax + b = 0
• Une équation du second degré se ramène à ax² + bx + c = 0
• Plus généralement une équation polynomiale à a_nxⁿ + a_{n − 1}x^{n − 1} + ... + a₁x + a₀ = 0 ou P(x) = 0 avec P un polynôme
• Une équation différentielle fait intervenir une fonction inconnue f et ses dérivées en x, par exemple f''(x) − f(x) = 3
• Une équation fonctionnelle fait intervenir une fonction inconnue f et ses variables, mais en la composant avec des opérations, par exemple

Pour aller plus loin

• Équation

  Algèbre (mathématiques élémentaires) et Algèbre