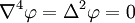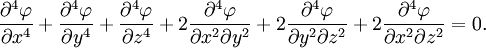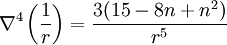Equation biharmonique

Equation biharmonique

Équation biharmonique

En analyse, l'équation biharmonique est une équation aux dérivées partielles d'ordre 4, qui apparaît par exemple dans la théorie de l'élasticité. L'équation biharmonique pour une fonction φ s'écrit :

\nabla^4\varphi= \Delta^2 \varphi = 0

où \nabla est l'opérateur nabla et Δ l'opérateur laplacien. L'opérateur Δ2 est aussi connu sous le nom d'opérateur biharmonique ou bilaplacien.

Dans le cas tridimensionnel, dans un système de coordonnées cartésiennes, l'équation biharmonique s'écrit :

\frac{\partial^4 \varphi}{ \partial x^4 } + \frac{\partial^4 \varphi}{ \partial y^4 } + \frac{\partial^4 \varphi}{ \partial z^4 }+ 2\frac{\partial^4 \varphi}{ \partial x^2\partial y^2}+ 2\frac{\partial^4 \varphi}{ \partial y^2\partial z^2}+ 2\frac{\partial^4 \varphi}{ \partial x^2\partial z^2} = 0.

Dans un espace euclidien de dimension n, la relation suivante est toujours vérifiée :

\nabla^4 \left(\frac{1}{ r}\right)= \frac{3(15-8n+n^2)}{ r^5}

avec r la distance euclidienne :

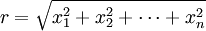r=\sqrt{x_1^2+x_2^2+\cdots+x_n^2}.

ce qui, pour n = 3, est solution de l'équation biharmonique.

Une fonction qui est solution de l'équation biharmonique est appelée fonction biharmonique. Toute fonction harmonique est biharmonique — la réciproque n'est pas vraie.

Voir aussi

Liens internes

Liens externes

Références

  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Biharmonic equation ».
  • Eric W Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 2002. ISBN 1-58488-347-2.
  • S I Hayek, Advanced Mathematical Methods in Science and Engineering, Marcel Dekker, 2000. ISBN 0-8247-0466-5.
  • J P Den Hartog, Advanced Strength of Materials, Courier Dover Publications, Jul 1, 1987. ISBN 0-486-65407-9.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « %C3%89quation biharmonique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equation biharmonique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Équation biharmonique — En analyse, l équation biharmonique est une équation aux dérivées partielles d ordre 4, qui apparaît par exemple dans la théorie de l élasticité. L équation biharmonique pour une fonction ϕ s écrit : où est l opérateur nabla et Δ l opérateur …   Wikipédia en Français

  • équation biharmonique — biharmoninė lygtis statusas T sritis fizika atitikmenys: angl. biharmonic equation vok. biharmonische Gleichung, f; Bipotentialgleichung, f rus. бигармоническое уравнение, n pranc. équation biharmonique, f …   Fizikos terminų žodynas

  • Opérateur biharmonique — Opérateur bilaplacien Articles d analyse vectorielle Ob …   Wikipédia en Français

  • biharmonic equation — biharmoninė lygtis statusas T sritis fizika atitikmenys: angl. biharmonic equation vok. biharmonische Gleichung, f; Bipotentialgleichung, f rus. бигармоническое уравнение, n pranc. équation biharmonique, f …   Fizikos terminų žodynas

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Bilaplacien — Opérateur bilaplacien Articles d analyse vectorielle Ob …   Wikipédia en Français

  • Operateur bilaplacien — Opérateur bilaplacien Articles d analyse vectorielle Ob …   Wikipédia en Français

  • Opérateur bilaplacien — L opérateur bilaplacien, ou opérateur biharmonique est, comme son nom le suggère, le nom donné à l opérateur laplacien appliqué deux fois. Expression Dans un système de coordonnées cartésiennes x1,x2,...xn, le bilaplacien s écrit . D autre part,… …   Wikipédia en Français

  • Fonction spéciale — Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques non élémentaires[1] …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”