- Epicycloïde
-
Épicycloïde
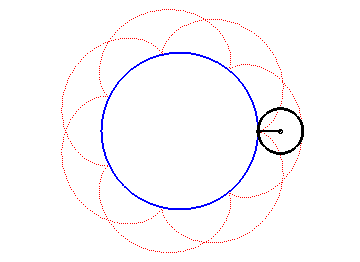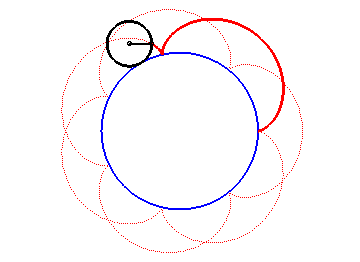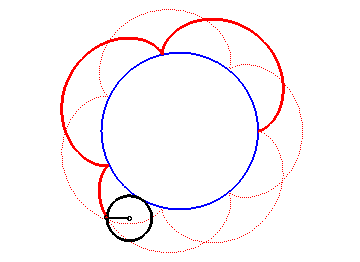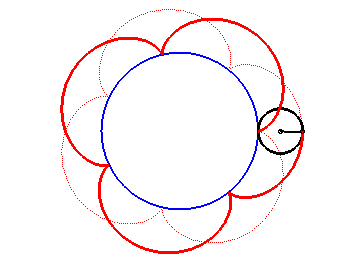 Construction d'une épicycloïde
Construction d'une épicycloïdeUne épicycloïde est une courbe plane transcendante, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un autre cercle dit directeur, les disques ouverts ayant ces deux cercles pour frontière étant disjoints. Il s'agit donc d'un cas particulier de cycloïde à centre, qui est une catégorie de courbe cycloïdale.
Sommaire
Étymologie et histoire
Le mot est une extension de cycloïde, inventé en 1599 par Galilée, et a la même étymologie : il vient du grec epi (sur), kuklos (cercle, roue) et eidos (forme, « semblable à »).
La courbe apparaît pour la première fois durant l'Antiquité : Aristote puis Ptolémée l'utilisent pour décrire le mouvement des planètes dans leur modèle géocentrique, et pour résoudre les problèmes liés aux rebroussements qui apparaissent dans leur trajectoire céleste, que l'on appelle rétrogradation. Cependant, la courbe en elle-même n'est pas évoquée ; elle est seulement une conséquence du mouvement suivant une épicycle tournant autour d'un déférant.
Au cours de ses travaux sur les profils des dents engrenages, Rømer redécouvre l'épicycloïde et la baptise en 1674. Il prouve alors qu'en dessinant les dents d'un engrenage avec des segments d'épicycloïde, deux roues d'engrenages tournent avec une friction minimale. Ces résultats sont confirmés par la suite par Girard Desargues, Philippe de La Hire et Charles Stephen. Le théorème de la double génération de la courbe, quant à lui, est démontré pour la première fois par Daniel Bernoulli en 1725.
Parmi les autres mathématiciens qui se sont intéressés à cette courbe, citons Durer, Huygens, Leibniz, L'Hôpital, Jacques Bernoulli, Euler, Edmond Halley et Isaac Newton, ce dernier ayant traité de la mesure de la longueur de l'épicycloïde dans son Philosophiae Naturalis Principia Mathematica.
Définition mathématique
Une épicycloïde peut être définie par l'équation paramétrique suivante :
où
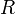 est le rayon du cercle de base et
est le rayon du cercle de base et  celui du cercle roulant. Avec
celui du cercle roulant. Avec 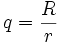 , cette équation peut donc également s'écrire :
, cette équation peut donc également s'écrire :Propriétés
La courbe est formée d'arcs isométriques (appelés arches) séparés par des points de rebroussements. Si q est rationnel (et peut donc s'écrire q=a/b où a et b sont des entiers), a représente le nombre d'arches de la courbe. On peut aussi voir ces deux grandeurs de la manière suivante :
- a représente le nombre de rotations du cercle roulant nécessaires pour ramener le point mobile à sa position de départ,
- b représente le nombre de tours du cercle de base nécessaires au cercle roulant pour revenir au point de départ.
Les points de rebroussements sont obtenus pour
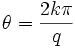 . La longueur d'une arche est de
. La longueur d'une arche est de 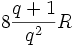 .
.
Si q est entier, la longueur totale de la courbe vaut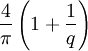 fois la longueur du cercle de base, et l'aire totale vaut
fois la longueur du cercle de base, et l'aire totale vaut 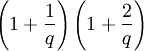 fois celle du cercle de base.
fois celle du cercle de base.Le théorème de la double génération prouve qu'une épicycloïde est aussi une péricycloïde de paramètre q'=q/(q+1), c'est-à-dire la courbe décrite par un point d'un cercle de rayon r+R roulant sans glisser sur ce cercle directeur en le contenant.
Comme Ptolémée avant eux, les astronomes rencontrent souvent l'épicycloïde dans leur étude des des mouvements célestes, lorsqu'ils simplifient les orbites ellipsoïdales en orbites circulaires.
Quelques exemples

q = 1 : cardioïde
q = 2 : néphroïde
q = 3
q = 4
q = 5
q = 1/2
q = 3/2
q = 5/2
q = 7/2
q = 9/2
q = 1/3
q = 2/3
q = 4/3
q = 5/3
q = 7/3
q = 1/4
q = 3/4
q = 5/4
q = 7/4
q = 9/4
q = 1/5
q = 2/5
q = 3/5
q = 4/5
q = 6/5Voir aussi
- Lorsque le point mobile n'est pas fixé sur le cercle roulant mais à l'extérieur ou à l'intérieur de celui-ci on parle alors d'épitrochoïde, qui est un cas particulier de trochoïde. D'ailleurs, si vous avez cru reconnaître les dessins réalisés avec un spirographe dans les illustrations ci-dessus, vous ne vous êtes pas beaucoup trompé : cet appareil réalise des épitrochoïdes et non des épicycloïdes.
- Lorsque le cercle mobile tourne à l'intérieur du cercle directeur, la courbe ainsi dessinée s'appelle alors hypocycloïde.
Liens externes
- Sur le site MathCurve.com
- Une Applet qui permet de jouer avec les paramètres de construction d'une épicycloïde
- Portail de la géométrie
Catégorie : Courbe
Wikimedia Foundation. 2010.

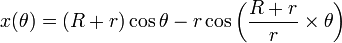
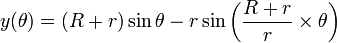
![x(\theta) = r \left[(q+1) \cos \theta - \cos ((q+1)\times \theta) \right] \,](/pictures/frwiki/50/2d92001325258b47b8d095850d6a270c.png)
![y(\theta) = r \left[(q+1) \sin \theta - \sin ((q+1)\times \theta) \right]\,](/pictures/frwiki/56/85e6205ab88ba5253b6c50e00095eac3.png)