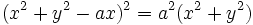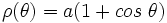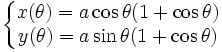Cardioide

Cardioide

Cardioïde

Construction de la cardioïde

La cardioïde est une courbe algébrique plane, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un second cercle de même diamètre. Il s'agit donc d'une courbe cycloïdale dont la directrice est un cercle (ou épicycloïde).

Sommaire

Étymologie et histoire

Son nom vient du grec kardia (cœur), en référence à sa forme, et lui fut donné par Johan Castillon.

D'abord étudiée comme un cas particulier du limaçon de Pascal, la première évocation de la cardioïde en tant qu'épicycloïde remonte à 1674 : Rømer l'étudia au cours de ses recherches sur la forme la plus adaptée aux dents des engrenages. En 1708, La Hire détermina son périmètre (8 fois le diamètre du cercle directeur). Castillon la décrit plus en détail et la baptisa dans un document qu'il publia en 1741. Néanmoins, comme il s'agit d'un cas particulier de limaçon de Pascal (courbe étudiée par Étienne Pascal, le père de Blaise), on peut dire que son histoire commence bien avant les travaux de La Hire et Castillon.

Définition mathématique

4 cardioïdes orientées selon les quatre directions cardinales

La courbe peut être définie par l'équation cartésienne suivante :

(x^2+y^2-ax)^2=a^2(x^2+y^2)\,

On peut également la définir par une équation polaire :

\rho ( \theta ) =a(1+cos\ \theta )\,

.. ou par une équation paramétrique :

\left\{\begin{matrix} x(\theta) = a \cos \theta (1 + \cos \theta ) \\ y(\theta) = a \sin \theta (1 + \cos \theta)\end{matrix}\right.

Propriétés et applications

Géométrie

La cardioïde est :

  • une conchoïde de cercle relativement à un point situé sur le cercle, avec une raison égale au diamètre du cercle. Il s'agit donc d'un cas particulier de limaçon de Pascal
  • une podaire de cercle par rapport à l'un de ses points
  • une inverse de parabole par rapport à son foyer

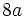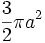Le périmètre d'une cardioïde formée à partir d'un cercle de diamètre a\, vaut 8a\, ; son aire vaut \frac{3}{2} \pi a^2.

Comme pour toute courbe cycloïdale, la développée de la cardioïde est une cardioïde homothétique.

Optique

Cardioïde apparaissant nettement dans une cocotte en fonte

La cardioïde est une caustique de cercle par réflexion avec source lumineuse sur le cercle. Cette propriété explique que la forme dessinée au fond d'un récipient par la réflexion des rayons lumineux provenant d'une source ponctuelle proche du bord du récipient soit une cardioïde.

Attention, lorsque le récipient est opaque et que ce sont les rayons parallèles du soleil qui se reflètent à l'intérieur, on distingue une forme comparable mais il s'agit alors d'une autre épicycloïde, la néphroïde.
D'ailleurs, la caustique par réflexion de la cardioïde, avec la source lumineuse au point de rebroussement de la cardioïde, est une néphroïde.

Acoustique

On dit d'un microphone qu'il est cardioïde lorsque sa sensibilité varie en fonction de la position de la source par rapport à l'axe du micro en dessinant une courbe cardioïde. En fait ce terme est synonyme de microphone unidirectionnel. les microphones cardioïdes favorisent la présence de la source sonore frontale et atténuent fortement les sons latéraux et arrières. Le microphone cardioïde est particulièrement adapté à l'enregistrement de la voix et des instruments de musique. Le contraire d'un microphone cardioïde est un microphone omnidirectionnel. Quand le microphone atténue fortement tous les sons qui ne sont pas exactement dans l'axe, on le dit hypercardioïde.

Divers

On trouve une cardioïde au centre d'une fractale très connue, l'ensemble de Mandelbrot.

Voir aussi

Liens externes

Exemples de courbes
Coniques (cercle, ellipse, parabole, hyperbole)
Cardioïde • Cissoïde • Clothoïde • Cycloïde • Épicycloïde • Folium de Descartes • Hélice • Hypocycloïde (astroïde, deltoïde) • Hypotrochoïde • Spirale (d'Archimède, logarithmique)
Lemniscates (lemniscate de Gerono, lemniscate de Booth, lemniscate de Bernoulli, courbe du diable)
Trajectoire • Ovale de Cassini • Chaînette • Courbe brachistochrone
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Cardio%C3%AFde ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cardioide de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • cardioïde — [ kardjɔid ] adj. • 1865; de cardio et ide ♦ Didact. En forme de cœur. N. f. Math. Cycloïde à point de rebroussement lui donnant une forme de cœur. ● cardioïde nom féminin Épicycloïde à un point de rebroussement dont l équation en coordonnées… …   Encyclopédie Universelle

  • Cardioide — Saltar a navegación, búsqueda Cardioide Se llama cardioide a la curva cuya ecuación polar es: ρ=a(1+cos θ), por su semejanza con el dibujo de un corazón. La cardioide es una curva ruleta del tipo epicicloide, con k=1; pero también es un caracol… …   Wikipedia Español

  • Cardioīde — (v. gr., Math.), eine Linie der 4. Ordnung von herzförmiger Gestalt, deren Gleichung zwischen rechtwinkeligen Coordinaten (y2 + x2)2 – 4rx (y2 + x2) – 4 r2y2 = 0 u. zwischen Polarcoordinaten u = 2r (1 + cos. t) ist. Wenn mau durch einen Punkt des …   Pierer's Universal-Lexikon

  • Cardioïde — Construction de la cardioïde La cardioïde est une courbe algébrique plane, trajectoire d un point fixé à un cercle qui roule sans glisser sur un second cercle de même diamètre. Il s agit donc d une courbe cycloïdale dont la directrice est un… …   Wikipédia en Français

  • cardioide — car·di·òi·de, car·diòi·de s.f. TS mat. curva algebrica piana della classe delle concoidi {{line}} {{/line}} DATA: 1865. ETIMO: dal gr. kardioeidēs a forma di cuore , der. di kardía cuore …   Dizionario italiano

  • cardioide — pl.f. cardioidi …   Dizionario dei sinonimi e contrari

  • Micrófono cardioide — Los micrófonos cardioides son micrófonos unidireccionales con un diagrama polar con forma de corazón (de ahí el nombre), lo que se traduce en una mayor sensibilidad hacia los sonidos que le llegan por su parte frontal y, por el contrario, un… …   Wikipedia Español

  • Micrófono cardioide — Los micrófonos cardioides son micrófonos unidireccionales con un diagrama polar con forma de corazón (de ahí el nombre), lo que se traduce en una mayor sensibilidad hacia los sonidos que le llegan por su parte fontral y, por el contrario, un… …   Enciclopedia Universal

  • ioïde — cardioïde …   Dictionnaire des rimes

  • Microphone — Pour les articles homonymes, voir Micro. Un microphone (ou plus simplement micro par apocope) est un dispositif de conversion des ondes sonores acoustiques d un milieu compressible en impulsions électriques. C est donc un capteur analogique. Le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”