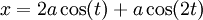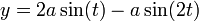Deltoide (courbe)
- Deltoide (courbe)
-
Deltoïde (courbe)
La courbe en rouge est une deltoïde.
La deltoïde n'est autre qu'une hypocycloïde à trois rebroussements. Elle fut étudiée pour la première fois par Léonard Euler en 1745.
Équations cartésiennes
En écrivant la position du point d'un cercle de rayon a roulant sans glisser à l'intérieur d'un cercle de rayon 3a, on obtient l'équation paramétrique suivante :
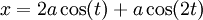
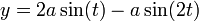

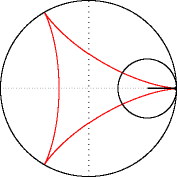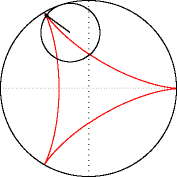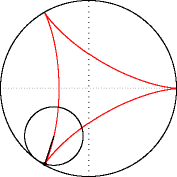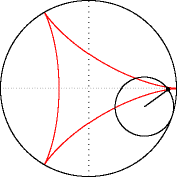
La deltoïde comme enveloppe d'
un segment dont les extrémités sont astreintes à suivre la courbe
L'équation cartésienne est de la forme :
- (x2 + y2)2 + 18(x2 + y2) = 8x3 − 24y2x + 27
ce qui montre que cette courbe est algébrique de degré 4. Elle possède trois points singuliers (les trois points de rebroussement), et elle est de genre zero.
Propriétés géométriques
- Une règle dont les deux extrémités sont astreintes à glisser sur la deltoïde vient tangenter la deltoïde en un troisième point : le point de tangence décrit deux fois la deltoïde lorsque les extrémités ne la décrivent qu'une fois.
- L'enveloppe des droites de Simson d'un triangle est une deltoïde (théorème dû à Jakob Steiner).
- La développante de la deltoïde a pour équation cartésienne
- x3 − x2 − (3x + 1)y2 = 0, Elle présente un point double à l'origine, ce que l'on peut vérifier en opérant une rotation imaginaire y → iy, qui aboutit à l'équation :
x3 − x2 + (3x + 1)y2 = 0 courbe qui présente un point double à l'origine dans 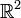 .
.
Références
- Jacques Hadamard - On the three-cusped hypocycloid (1945), Mathematical Gazette, vol. 29, pp. 66-67
Voir aussi
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Deltoide (courbe) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Deltoïde (Courbe) — La courbe en rouge est une deltoïde. La deltoïde n est autre qu une hypocycloïde à trois rebroussements. Elle fut étudiée pour la première fois par Léonard Euler en 1745. Sommaire 1 Équations cartésiennes … Wikipédia en Français
Deltoïde (courbe) — La courbe en rouge est une deltoïde. La deltoïde n est autre qu une hypocycloïde à trois rebroussements. Sa forme ressemble un peu à celle de la lettre grecque delta, d où son nom. Cet exemple de roulette (en) fut étudié pour la première… … Wikipédia en Français
Courbe Plane — En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue : où I est un intervalle de l ensemble des nombres réels. L image d une courbe est aussi… … Wikipédia en Français
Deltoide — Deltoïde Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Deltoïde peut signifier : Un muscle deltoïde, un des muscles de l épaule. Une courbe géométrique : deltoïde. Ce document provient de «… … Wikipédia en Français
Courbe Brachistochrone — Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes … Wikipédia en Français
Courbe brachystochrone — Courbe brachistochrone Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de… … Wikipédia en Français
Courbe Du Diable — avec les paramètres a=√10/10 et b=3×a. La courbe du diable a été étudiée en 1750 par Cramer et en 1810 par Lacroix. Sommaire … Wikipédia en Français
Courbe du diable — avec les paramètres a=√10/10 et b=3×a … Wikipédia en Français
Courbe Cycloïdale — Construction d une épicycloïde Une courbe cycloïdale est une courbe plane transcendante, trajectoire d un point fixé à un cercle qui roule sans glisser sur une courbe dite directrice. Il s agit donc d un cas particulier de roulette. Sommaire 1… … Wikipédia en Français
Courbe cycloidale — Courbe cycloïdale Construction d une épicycloïde Une courbe cycloïdale est une courbe plane transcendante, trajectoire d un point fixé à un cercle qui roule sans glisser sur une courbe dite directrice. Il s agit donc d un cas particulier de… … Wikipédia en Français
 La courbe en rouge est une deltoïde.
La courbe en rouge est une deltoïde. La deltoïde comme enveloppe d'un segment dont les extrémités sont astreintes à suivre la courbe
La deltoïde comme enveloppe d'un segment dont les extrémités sont astreintes à suivre la courbe
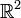 .
.