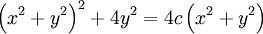Lemniscate De Booth
- Lemniscate De Booth
-
Lemniscate de Booth
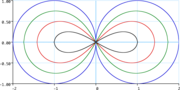
Lemniscates de Booth, pour différentes valeurs de
c.
c = 0,25 (noir)
c = 0,5 (rouge)
c = 0,75 (vert)
c = 1 (bleu).
En géométrie algébrique, la lemniscate de Booth, aussi appelée courbe de Booth, ovale de Booth ou encore hippopède de Proclus, est une lemniscate du plan euclidien. Elle est généralisée dans l'espace par les surfaces d'élasticité de Fresnel.
Elle est définie comme l'ensemble des points solutions de l'équation :
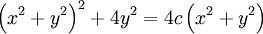
avec (x, y) les coordonnées cartésiennes du point et c un paramètre réel.
Lorsque c > 1, on observe une figure fermée, appelée ovale de Booth. Lorsque c < 1, elle forme le lemniscate de Booth. Lorsque c = 1, elle se réduit à deux cercles tangents. Enfin, pour c < 0, la figure est réduite à un unique point coïncidant avec l'origine.
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Lemniscate De Booth de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Lemniscate de booth — Lemniscates de Booth, pour différentes valeurs de c. c = 0,25 (noir) c = 0,5 (rouge) c = 0,75 (vert) c = 1 (bleu). En géométrie algébrique, la lemniscate de Booth, aussi appelée courbe de Booth, ovale de Booth ou encore hippopède de Proclus, est… … Wikipédia en Français
Lemniscate de Booth — Lemniscates de Booth, pour différentes valeurs de c. c = 0,25 (noir) c = 0,5 (rouge) c = 0,75 (vert) c = 1 (bleu). En géométrie algébrique, la lemniscate de Booth, aussi appelée courbe de Booth, ovale de Booth ou encore hippopède de Proclus, est… … Wikipédia en Français
Lemniscate of Booth — In algebraic geometry, the lemniscate of Booth, also called the Hippopede of Proclus , is a plane algebraic curve of degree four and genus zero, with equation:(x^2+y^2)^2 + 4y^2 = 4c(x^2+y^2),.It has an ordinary double point at the origin, and… … Wikipedia
Lemniscate De Bernoulli — La lemniscate de Bernoulli. La lemniscate de Bernoulli est une courbe plane. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli. Une lemniscate de Bernoulli, de foyers F et F’, est l ensemble des points M vérifiant la… … Wikipédia en Français
Lemniscate de bernoulli — La lemniscate de Bernoulli. La lemniscate de Bernoulli est une courbe plane. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli. Une lemniscate de Bernoulli, de foyers F et F’, est l ensemble des points M vérifiant la… … Wikipédia en Français
Lemniscate De Gerono — La Lemniscate de Gerono est une courbe plane, qui a été étudiée par Grégoire de Saint Vincent en 1647 puis Cramer en 1750. Équations Paramétrisation cartésienne : . Équation algébrique … Wikipédia en Français
Lemniscate de gerono — La Lemniscate de Gerono est une courbe plane, qui a été étudiée par Grégoire de Saint Vincent en 1647 puis Cramer en 1750. Équations Paramétrisation cartésienne : . Équation algébrique … Wikipédia en Français
Lemniscate — Une lemniscate est une courbe plane ayant la forme d un 8. Elle possède deux axes de symétrie perpendiculaires. Ceux ci se coupent en un point double de la courbe, également son centre de symétrie. Sommaire 1 Étymologie et histoire 2 Autres… … Wikipédia en Français
Booth — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Booth peut désigner : Patronyme Booth est un nom de famille notamment porté par : Felix Booth (1775 1850), homme d affaires britannique ;… … Wikipédia en Français
Lemniscate de Bernoulli — La lemniscate de Bernoulli. La lemniscate de Bernoulli est une courbe plane unicursale. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli. Une lemniscate de Bernoulli, de foyers F et F’, est l ensemble des points M… … Wikipédia en Français