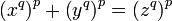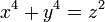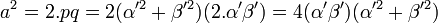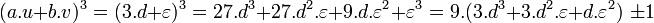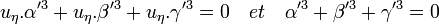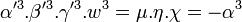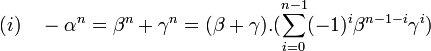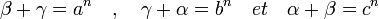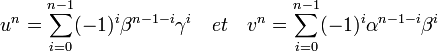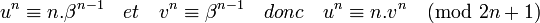Démonstration du dernier théorème de Fermat

Démonstration du dernier théorème de Fermat

Démonstrations du dernier théorème de Fermat

Pierre de Fermat

En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l'équation diophantienne suivante, d'inconnues x, y et z :

n \in \mathbb{N}\quad x^n + y^n = z^n\;

Il stipule qu'il n'existe aucune solution non triviale si le paramètre n est strictement supérieur à deux.

Une équation diophantienne est une équation à coefficients entiers dont les solutions recherchées sont entières. Si, à l'exemple de la question de l'article, l'expression est souvent simple, la résolution s'avère en général ardue.

En 1637 Pierre de Fermat (1601 - 1665) propose cette équation et indique dans la marge de son exemplaire du livre Arithmetica de Diophante qu'il a trouvé une merveilleuse démonstration.

Il est peu probable qu'une démonstration accessible à Fermat existe. En effet, il faut de nombreuses tentatives ainsi que près de 350 ans d'efforts pour qu'une preuve en soit donnée en 1994 par Andrew Wiles.

Sommaire

Généralités et cas élémentaires

Remarques

L'équation est homogène, c’est-à-dire que pour une valeur n donnée, si le triplet (x, y, z) est solution, alors (a.x, a.y, a.z) est aussi solution. En conséquence, les seules racines recherchées sont les triplets d'entiers premiers entre eux dans leur ensemble.

Si l'un des trois membres du triplet (x, y, z) est égal à zéro, alors l'équation devient évidente, de telles solutions sont dites triviales. L'objectif est donc la recherche de triplet solution tel que le produit x.y.z soit différent de zéro.

Si l'équation n'admet pas de solution pour une valeur p du paramètre, alors il n'existe pas de solution pour toute valeur n multiple de p. En effet, si l'on note n = p.q alors l'équation s'écrit:

\left( x^q \right)^p + \left( y^q \right)^p = \left( z^q \right)^p\;

En conséquence, les valeurs à traiter sont celles où n est un nombre premier. Il est toutefois à noter l'unique exception, correspondant au cas où n est égal à deux. En effet, des solutions existent, il est donc nécessaire d'étudier aussi le cas où n est égal à quatre.

Résultats sans appel à la théorie des nombres

Quelques résultats se démontrent sans structure complexe. Le cas où n est égal à deux, traité à la suite, est simple et date de l'antiquité. Celui où n est égal à quatre se démontre de manière un tout petit peu moins élémentaire. Les cas restant sont ceux où n est premier différent de deux. Il existe une démonstration qui n'utilise pas les entiers d'Eisenstein pour le cas où n est égal à trois, elle est néanmoins suffisamment astucieuse et difficile pour que le mathématicien Leonhard Euler ne propose qu'une démonstration inexacte.

Les autres cas sont techniques, l'utilisation d'entiers algébriques est indispensable. Le premier terme est bien une identité remarquable : xn + yn est en effet un multiple de x + y si n n'est pas une puissance de deux, cependant cette remarque est largement insuffisante pour conclure ne serait-ce que dans un cas.

Cas où n est égal à deux

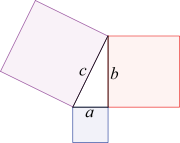
Article détaillé : Triplet pythagoricien.
Le théorème de Pythagore: a2 + b2 = c2

Le cas où n est égal à deux possède une interprétation géométrique. Il correspond aux longueurs entières des différents cotés d'un triangle rectangle.

Ce cas est connu depuis la haute antiquité. Ainsi, les sumériens connaissaient[1] quelques exemples de solutions. La solution complète apparaît pour la première fois dans le livre X des Eléments[2] d'Euclide vers 300 av. J.-C.

Ce cas est l'unique exception du théorème (si l'on omet le cas où n est égal à un). En effet, il existe des solutions non triviales si n est égal à deux : 3, 4 et 5 forment un triplet de solutions, appelé triplet pythagoricien. En conséquence, il devient important de considérer le cas n égal à quatre, pour démontrer qu'il n'existe pas d'autre puissance de deux admettant des solutions non triviales.

Une démonstration est donnée dans l'article Triplet pythagoricien.

Cas où n est égal à quatre

Ce cas est probablement l'unique traité par Fermat. Si aucune preuve écrite n'est trouvée dans sa correspondance, en revanche il démontre qu'il n'existe aucun triplet pythagoricien tel que x.y/2 soit un carré d'entier, ce qui s'exprime, dans le vocabulaire de l'auteur par l'aire d'un triangle rectangle ne peut être celle d'un carré. À partir de ce résultat, la démonstration est aisée. Pour cette raison, Fermat est très généralement considéré comme l'auteur de cette démonstration[3],[4].

La méthode utilisée est celle de la descente infinie. La méthode consiste à trouver un autre triplet de solutions tel que le troisième entier est positif et strictement plus petit que celui de la solution initiale. Il est ainsi possible descendre indéfiniment dans l'ensemble des entiers positifs, ce qui est contradictoire avec les propriétés de N.

Une preuve complète et nouvelle provient de Leonhard Euler (1707 - 1783), elle est aussi fondée sur la méthode de la descente infinie. Il en existe d'autres, par exemple utilisant la notion d'entiers de Gauss.


Démonstration du cas n = 4

Etudions les solutions entières non triviales (c’est-à-dire tel que le produit x.y.z soit différent de zéro) de l'équation :

x^4+y^4=z^2\;

L'équation de Fermat se déduit simplement de la résolution de l'équation précédente. Supposons l'existence d'un triplet de solutions premières entre elles dans leur ensemble et non triviales (a, b, c) avec c strictement positif et montrons alors qu'il existe un autre triplet de solutions non triviales (α, β, γ) tel que γ est positif et strictement plus petit que c. Le théorème de la descente infinie permet alors de conclure.

Le cas où n est égal à deux montre l'existence d'une paire d'entiers premiers entre eux p et q tel que:

a^2=2.pq\quad , \quad b^2 = p^2-q^2 \quad et \quad c = p^2+q^2\;

L'égalité q 2 + b 2 = p 2 montre l'existence d'un couple d'entiers premiers entre eux (α', β') tel que:

q=2.\alpha' \beta' \quad , \quad b = \alpha'^2-\beta'^2 \quad et \quad p = \alpha'^2+\beta'^2\;

Les deux résultats précédents montrent que :

a^2=2.pq=2(\alpha'^2+\beta'^2)(2.\alpha'\beta' )=4(\alpha'\beta' )(\alpha'^2+\beta'^2)\;

Or α' et β' sont premiers entre eux, il en est donc de même pour α'.β' et α'2 + β'2 comme leur produit est un carré, ils sont chacun des carrés et donc il existe un entier γ strictement positif tel que γ2 = α4 + β4 où α2 est égal à α' et β2 est égal à β. Comme γ est plus petit que c la preuve est établie.

Entier quadratique

Article détaillé : Entier quadratique.

Une fois analysé le cas des puissances de deux, le théorème devient singulièrement plus complexe à établir. Il existe encore trois démonstrations, pour les cas n = 3, 5 et 7 fondées sur le même canevas et usant de la méthode de descente infinie.

Pour pouvoir l'appliquer, une idée fructueuse consiste à modifier l'ensemble sur lequel s'applique l'équation. Il est possible de généraliser le théorème de Fermat sur tout ensemble E muni de deux opérations l'addition et la multiplication. Les opérations sur E doivent disposer d'un minimum de propriétés, lui conférant une structure appelée anneau. Cette idée est un peu contre intuitive, si la résolution se révèle déjà ardue dans Z, l'anneau des entiers relatifs, la question ne devient-elle pas encore plus délicate sur un anneau quelconque ? En fait, l'objectif est de choisir E disposant des bonnes propriétés pour que la résolution soit plus aisée.

Cet anneau est choisi :

  • commutatif ;
  • unitaire, c'est-à-dire que la multiplication dispose d'un élément neutre 1 ;
  • intègre, c'est-à-dire que si un produit a.b est égal à 0 alors soit a soit b est nul ;
  • factoriel, ce qui signifie que tout élément se décompose de manière unique en un élément inversible pour la multiplication et un produit de nombres premiers, comme -6 est le produit de -1, 2 et 3 ;
  • et tel que tout élément inversible possède une racine nième.

Sur un tel anneau, correspondant par exemple à celui des polynômes à coefficients dans C, l'ensemble des nombres complexes, Augustin Louis Cauchy met au point une méthode générale de résolution.

La difficulté réside dans le fait que Z ne contient pas de racine nième de l'unité à l'exception de 1 et -1. L'usage d'autres anneaux contenant Z devient intéressant. Les plus simples correspondent à des ensembles Z[ω] d'entiers quadratiques c'est-à-dire des nombres de la forme a + bω où a et b sont des entiers relatifs et ω un nombre complexe tel que ω2 soit combinaison linéaire de ω et de 1 à coefficients dans Z, ce qui assure la stabilité de l'ensemble. Certains de ces ensembles contiennent des racines nième de l'unité. Tel est le cas si ω est la racine cubique de l'unité j = 1/2(1 + i√3) ou le nombre d'or 1/2(1 + √5). De plus, ces anneaux sont dit euclidiens, c'est-à-dire qu'il existe une division euclidienne. Et tout anneau euclidien est factoriel. Ils permettent de résoudre les cas n = 3 ou 5. Une approche un peu analogue permet encore de résoudre le cas n = 7.

L'efficacité des anneaux quadratiques s'arrête là. Dans le cas général, ils ne sont ni euclidiens ni factoriels, ce qui impose la mise au point d'autres idées.

Cas de l'anneau des polynômes à coefficients complexes

Augustin Louis Cauchy.

On recherche ici à résoudre l'équation :

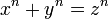
x^n + y^n = z^n\;

Ici x, y et z représentent trois polynômes à coefficients complexes. Pour les raisons indiquées au paragraphe précédent, cette question est finalement beaucoup plus facile que celle de Fermat. Elle est résolue en 1847 Par Cauchy[5] après la résolution des cas n = 3,5 et 7 et avant la percée majeur de Ernst Kummer. Le résultat s'énonce de la manière suivante :

  • Soit p, q, r trois polynômes à coefficients complexes et n un entier strictement plus grand que 2, si pn + qn = rn et si p, q et r sont premiers entre eux, alors p, q et r sont trois polynômes constants.

Deux polynômes sont dit premiers entre eux si, et seulement si, les seuls polynômes qui divisent les deux sont les constantes. Cette résolution est plus simple que les trois cas précédents car la complexité calculatoire est moindre. La démarche est néanmoins très similaire. L'ensemble des polynômes à coefficients dans C forment un anneau commutatif unitaire et intègre équipé d'une division euclidienne. Une démarche de nature arithmétique est ainsi possible. Il existe un équivalent de la notion de nombre premier, celle de polynôme irréductible (c'est-à-dire divisible uniquement par lui-même et par 1, à la multiplication par un nombre complexe près) et unitaire (c'est-à-dire de coefficient du terme de plus haut degré égal à 1). Le théorème fondamental de l'arithmétique s'applique, c'est-à-dire qu'il existe une unique décomposition en facteurs premiers, ainsi que l'identité de Bézout ou le lemme d'Euclide. Les démonstrations présentées dans cet article pour les cas n égal à 3 ou 5 sont choisies dans le cadre d'un anneau euclidien.

Cette anneau possède une force qui simplifie largement la démonstration, tout élément du groupe des unités, c'est-à-dire le groupe des éléments inversibles pour la multiplication admet une racine nième. Le fait que les éléments du groupe des unités ne soient pas inversibles présente encore la difficulté à contourner pour les cas n égal 3 et 5.

Démonstration

La démonstration utilise encore une fois la méthode de descente infinie. On suppose qu'il existe d'autres solutions que celles des polynômes constants et on considère un triplet de polynômes (p, q, r) de cette nature soit n0 la somme de leur degré. À l'aide de cette solution, on en construit une nouvelle (p1, q1, r1) tel que la somme des degrés n1 est strictement positive et strictement inférieure à n0. En réitérant le processus, on obtient une suite infinie et strictement décroissante (nj) d'entiers positifs. La méthode de descente infinie procure la contradiction recherchée.

La lettre ζ désigne une racine primitive de l'unité, c'est-à-dire une racine telle que l'ensemble des nombres ζj, si j varie de 0 à n - 1, décrivent toutes les racines nièmes de l'unité. Le polynôme Xn - 1 possède exactement n racines distinctes qui sont les n racines de l'unité, ce qui permet de déduire les égalités :

X^n - 1 = \prod_{j=0}^{n-1} (X - \zeta^j)\quad\text{donc}\quad \forall a,b \in \mathbb C[X]\quad a^n - b^n = b^n (\left(\frac ab\right)^n - 1) = b^n\prod_{j=0}^{n-1}(\frac ab - \zeta^j) = \prod_{j=0}^{n-1}(a - \zeta^jb)

L'équation de Fermat s'écrit encore :

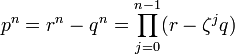
p^n = r^n - q^n = \prod_{j=0}^{n-1}(r - \zeta^jq)

Cette factorisation est possible dans tous les anneaux commutatifs unitaires intègres contenant les n racines nièmes de l'unité.

Le caractère factoriel intervient maintenant dans la démonstration. On remarque que les polynômes r - ζjq sont premiers deux à deux. Deux polynômes de cette nature engendrent en effet l'espace vectoriel de base r et q. Un diviseur communs divise donc r et q et par hypothèse est constant. Chaque facteur premier de r - ζjq est un facteur premier de pn donc de p et se trouve nécessairement à la puissance n dans le polynôme r - ζjq puisqu'il n'est pas présent dans les polynômes r - ζkq si k est différent de j. On en déduit que le polynôme r - ζjq est une puissance nième et qu'il existe un polynôme aj tel que ajn est égal à r - ζjq. On obtient l'égalité :

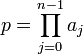
p = \prod_{j=0}^{n-1} a_j

On remarque que les polynômes aj sont premiers entre eux deux à deux,car les polynômes r - ζjq le sont et une analyse de leur monôme dominant montre que l'un au plus est constant. Considérons les trois polynômes a1, a2 et a3. Leur puissance nième est dans l'espace vectoriel engendré par r et q, de dimension deux. Il existe donc une combinaison linéaire non triviale entre eux trois.

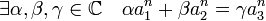
\exists \alpha,\beta,\gamma \in \mathbb C \quad \alpha a_1^n + \beta a_2^n = \gamma a_3^n\;

Comme tout élément de C s'exprime comme une puissance nième d'un élément de C, il existe trois complexes α1, β1 et γ1, tel que :

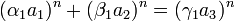
(\alpha_1 a_1)^n + (\beta_1 a_2)^n = (\gamma_1 a_3)^n\;

Ce qui montre l'existence de trois polynômes non tous constants, premiers deux à deux, de somme des degrés strictement inférieure à n0 satisfaisant l'équation initiale, offrant le cadre nécessaire à la mise en place de la méthode de descente infinie.[6]

 

Cas où n est égal à trois

Ferdinand Eisenstein
Article détaillé : Entier d'Eisenstein.

Le cas est plus complexe, Euler écrit à Goldbach en 1753, lui indiquant qu'il a résolu ce cas. Il publie[7] sa preuve, qui se révèle fausse[8]. Pour sa démonstration, il étudie des nombres dont le cube est de la forme p2 + 3.q2, pour cela il utilise une méthode originale pour l'époque, il considère l'ensemble Z[√3.i], et traite cet ensemble comme un anneau factoriel, c’est-à-dire qu'il suppose l'unicité d'une écriture d'un élément en éléments irréductibles. Ce résultat n'est pas exact, par exemple 4 est à la fois égal à 2 x 2 et aussi à (1 + √3.i)(1 - √3.i). Euler se penche à nouveau sur la question et finit par apporter une preuve satisfaisante[9].

Trente ans plus tard, Carl Friedrich Gauss (1777 1855) publie un traité[10] où, pour la première fois, un anneau d'entiers algébriques est étudié rigoureusement, l'anneau des entiers qui porte maintenant son nom. La logique de l'arithmétique modulaire devient applicable et une démonstration analogue à la première d'Euler est maintenant rigoureuse.

L'anneau d'entier algébrique permettant d'analyser simplement le cas où le paramètre est égal à trois est étudié précisément par Ferdinand Eisenstein (1823 1852). Cet ensemble est égal à Z[j] où j désigne la racine cubique de l'unité ayant une partie imaginaire pure strictement positive. Cet anneau est euclidien donc factoriel, en conséquence, la décomposition en éléments irréductibles aussi appelés nombres premiers d'Eisenstein est bien unique.

L'utilisation d'anneau d'entiers bien choisi est une des techniques majeures du XIXe siècle. Pour la résolution du théorème avec certains paramètres. En revanche, rares sont les anneaux d'entiers euclidiens. D'autres techniques doivent alors être adjointes pour arriver à une certaine généralité.

Dans cet anneau d'entiers appelés entiers d'Eisenstein, une descente infinie est relativement simple à trouver, c'est la méthode utilisée dans la preuve proposée ici.


Démonstration du cas n = 3

L'objectif est de résoudre l'équation : x3 + y3 = z' 3 dans l'anneau des entiers d'Eisenstein. En notant z = -z' , l'équation devient x3 + y3 + z3 = 0. Soit (α, β, γ) une solution non triviale tel que α, β et γ soient premiers entre eux dans leur ensemble.

Notons u = 1 + j et v = -j. On remarque que la famille (u, v) forme une base de l'anneau des entiers considéré comme un Z module. De plus, w = u - v est de norme égal à trois, c'est donc un nombre premier d'Eisenstein. Quelques calculs élémentaires montrent que u2 = -v, v2 = -u, u.v = u + v = 1 et u3 = v3 = -1. Dans la suite de la démonstration a et b désignent deux entiers relatifs.

1. a.u + b.v est un multiple de w si, et seulement si, a + b est un multiple de trois.

Si a.u + b.v est un multiple de w, alors il existe deux entiers relatifs n et m tel que:
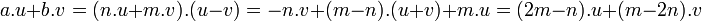
(i) \quad a.u+b.v=(n.u+m.v).(u-v)=-n.v+(m-n).(u+v)+m.u=(2m-n).u+(m-2n).v \;
On en déduit que a + b est égal à 3.(m - n). Réciproquement, si a + b est égal à 3.c, où c est un entier relatif, alors définissons m et n comme les deux entiers vérifiant n - m = c et 2.m - n = a, on vérifie que m - 2.n = b et les égalités (i) montrent que a.u + b.v est multiple de w.

2. Si a.u + b.v n'est pas un multiple de w, alors (a.u + b.v)3 est congru à plus ou moins un modulo neuf.

Soit da (respectivement db) le reste de la division euclidienne par trois de a (respectivement de b), d l'entier d'Eisenstein da.u + db.v et ε l'entier d'Eisenstein défini par a.u + b.v = 3.d + ε. Alors, si a.u + b.v n'est pas un multiple de w la proposition précédente montre que ε est élément de l'ensemble {±u, ±v, ±1}. Le calcul suivant permet de conclure :
(a.u+b.v)^3=(3.d + \varepsilon)^3=27.d^3+27.d^2.\varepsilon+9.d.\varepsilon^2+\varepsilon^3=9 .(3.d^3 +3.d^2.\varepsilon +d.\varepsilon^2)\; \pm 1 \;

3. Un et un seul des trois entiers d'Eisenstein α, β ou γ est un multiple de w.

La somme des trois cubes est égale à 0, elle est donc congrue à 0 modulo neuf. On en déduit que les trois cubes ne peuvent tous être congrus à ±1 modulo 9. La proposition précédente montre qu'au moins l'un d'entre eux est un multiple de w.
Si deux des trois entiers ont un diviseur commun, l'égalité α3 + β3 + γ3 = 0 montre que le troisième entier possède aussi ce diviseur. Le fait que les trois entiers soit premiers entre eux dans leur ensemble montre qu'ils sont premiers entre eux deux à deux, w n'est donc diviseur que de l'un des trois. Il est possible, sans perte de généralité de supposer que α est le multiple de w, cette hypothèse est celle de la suite de la démonstration.

4. α est un multiple de trois.

α est un multiple de w d'après le point 3. Donc β3 + γ3 qui est égal à -α3 est un multiple de w3. De plus, β3 (respectivement γ3) est congru à un élément de l'ensemble {±u, ±v, ±1} modulo 9 d'après le point 2, notons εβ (respectivement εγ) cet élément. β3 + γ3 est congru à εβ + εγ modulo 9, or 9 est un multiple de w3 car w4 est égal à 9. Ceci montre que εβ + εγ est congru à 0 modulo w3, ce qui montre que εβ + εγ est égal à 0.
εβ + εγ = 0, donc β3 + γ3 est congru à 0 modulo 9 et α3 est aussi congru à 0 modulo 9, ce qui montre que α est un multiple de trois.

5. Si μ = β.u + γ.v, η = β.v + γ.u et χ = β + γ, alors μ, η et χ sont des multiples de w.

Remarquons tout d'abord que β3 + γ3 = μ.η.χ. Ensuite w3 divise μ.η.χ car w3 divise α3 qui est égal à -β3 - γ3. Puis, w divise μ - η car μ - η = w.(β - γ) et enfin μ + η = β + γ est égal à χ.
Comme w divise μ.η.χ et que w est premier, il divise au moins l'un d'entre eux, par exemple μ. Comme w divise μ - η, il divise aussi η. Enfin comme w divise μ et η il divise χ = μ + η. Un raisonnement analogue permet de conclure de la même manière si w divise η ou χ.

6. Si μ', η', χ' sont définis par μ = w.μ', η = w.η' et χ = w.χ', alors μ', η' et χ' sont premiers deux à deux.

Raisonnons par l'absurde. Supposons que les trois entiers d'Eisenstein ne soit pas premiers entre deux deux à deux alors μ', η' ont un diviseur commun car χ' = μ'+ η'. Notons δ ce diviseur commun.
β + γ est égal à μ + η donc δ est un multiple de β + γ. β - γ est un multiple de μ - η (cf le point 6) donc δ est un multiple de β - γ. En conséquence, δ est un multiple de 2.β et de 2.γ. Comme β et γ sont premiers entre eux, δ est égal à deux (à un membre du groupe des unités près).
En conséquence β + γ et β - γ sont des multiples de deux. Divisons β et γ par deux, on obtient : β = 2.qβ + rβ et γ = 2.qγ + rγ, avec les normes de rβ et de rγ inférieures à trois. De plus comme β + γ est un multiple de deux rβ + rγ = 2.λ. En conséquence γ = 2.(qγ + λ) - rβ.
L'égalité μ = β.u + γ.v s'écrit alors μ = 2.(qβ.u + (qγ + λ).v + rβw. On remarque alors que deux est un nombre premier d'Eisenstein qui ne divise ni w si rβ qui est le reste d'une division euclidienne par deux. En conclusion μ n'est pas un multiple de deux, μ' non plus ce qui est une contradiction.

7. Il existe un triplet de racine cubique de μ', η' et -χ' solutions de l'équation de Fermat à un élément du groupe de l'unité près.

L'égalité μ'.η'.χ' = θ3 où θ est défini par θ.w = α (le point 3. montre que α est un multiple de w) et le fait que les éléments μ', η' et χ' sont premiers deux à deux montre que chacun des facteurs est le produit d'une unité et d'un cube.
\mu'=u_\mu.\alpha'^3\quad ,\quad \eta'=u_\eta.\beta'^3\quad et \quad \chi'=u_\chi.\gamma'^3 \;
L'égalité μ' + η' = χ' montre que uμ.α' 3 + uη.β' 3 - uχ.γ' 3 = 0.
L'égalité uμ.uη.uχ.(α'.β'.γ') 3 = θ3, montre que uμ.uη.uχ est un cube. Ce cube n'est pas multiple de w, il est donc congru à ±1 modulo 9. Il est donc égal à ±1.
Un et un seul élément parmi α', β' et γ' est multiple de w. En effet, μ', η' et χ' sont premiers entre deux à deux, il en est donc de même avec α', β' et γ'. En conséquence au plus un élément est multiple de w. Le point 4 montre que α est multiple de 3 qui est égal à w2, et θ est un multiple de w. Comme w est un nombre premier d'Eisenstein, il divise au moins l'un des trois membres. Par la suite, on suppose que α' est le multiple de w. Le raisonnement est le même si le multiple s'avère être l'un des deux autres membres.
β' et γ' ont un cube congru à ±1 modulo 9 et un raisonnement analogue au point 4. montre que les racines uη et uχ sont opposées. L'égalité uμ.uη.uχ = 1 devient uμ.uη2 = ±1. Ce qui montre que uμ est égal à ± uη. Quitte à modifier le signe de α', il est toujours possible de choisir uμ égal à uη. L'égalité devient:
u_\eta.\alpha'^3 + u_\eta.\beta'^3 + u_\eta.\gamma'^3 = 0 \quad et \quad \alpha'^3 + \beta'^3 + \gamma'^3 = 0 \;

8. Une descente infinie montre qu'il n'existe pas de solution à l'équation de Fermat si n est égal à trois.

Le premier triplet de solutions (α, β, γ) non trivial est tel que le produit α.β.γ contient le facteur w plusieurs fois (au moins deux d'après le point 4.). Un tel triplet montre l'existence d'un deuxième triplet de solutions (α', β', γ' ) non trivial tel que le produit α'.β'.γ' contient le facteur w un nombre de fois strictement inférieur car β et γ ne sont pas multiples du nombre premiers d'Eisenstein w et que :
\alpha'^3 . \beta'^3 . \gamma'^3.w^3 = \mu.\eta.\chi = -\alpha^3\;
Ceci démontre l'existence d'une descente infinie et donc l'absence de solution.

Théorème de Sophie Germain

La démarche permettant de résoudre le cas où n est égal à trois ne se généralise pas. En effet, l'anneau des entiers algébriques associé aux racines de l'unités n'est plus factoriel. Le raisonnement arithmétique du cas précédent n'est donc plus opérationnel.

Durant la première décennie du XIXe siècle, Sophie Germain (1776 - 1831) apporte une nouvelle idée appelée

Théorème de Sophie Germain : Si n > 2 et 2n + 1 sont des nombres premiers et si x.y.z n'est pas multiple de n, alors le triplet (x, y, z) n'est pas solution de l'équation de Fermat.

La démonstration du cas où le paramètre est égal à trois utilise une démarche de cette nature.

L'étude de la démonstration du théorème est alors divisée en deux cas:

  • Il existe une valeur du triplet multiple de n.
  • Aucun des membres n'est multiple de n.

Sophie Germain résout le premier cas pour toutes les valeurs du paramètre inférieures à cent. Adrien-Marie Legendre (1752 - 1833) pousse la démonstration à toutes les valeurs plus petites que cent-quatre-vingt-dix-sept.


Démonstration du théorème de Sophie Germain

n est impair. En conséquence, en modifiant le signe de z, l'équation s'écrit x n + y n + z n = 0. Soit (α, β, γ) une solution non triviale tel que α, β et γ soient premiers entre eux dans leur ensemble, et donc deux à deux. Montrons que α.β.γ est une puissance de n. Pour cela, raisonnons par l'absurde : supposons que α.β.γ ne soit pas une puissance de n et trouvons une contradiction.

1. α + β, β + γ et γ + α sont des puissances de n.

L'équation s'écrit de la manière suivante:
(i)\quad -\alpha^n=\beta^n+\gamma^n=(\beta + \gamma).(\sum_{i=0}^{n-1} (-1)^i\beta^{n-1-i}\gamma^i)\;
Montrons que β + γ et β n-1 - β n-2.γ + ... + γ n-1 sont premiers entre eux. Soit d un diviseur des deux membres. Alors γ est congru à -β modulo d et le deuxième terme est congru à zéro modulo d. En remplaçant γ par -β dans le deuxième terme, on montre que n. β n-1 est un multiple de d. Ceci montre que β est un multiple de d. Comme β + γ l'est aussi, γ est un multiple de d. Comme β et γ sont premiers entre eux, on en déduit que d est égal à 1.
Les deux facteurs de droite de l'égalité (i) sont premiers entre eux et leur produit est égal à une puissance de n. Ceci montre que β + γ est une puissance de n. Le même raisonnement s'applique pour α + β et γ + α. Il existe donc trois entiers a, b et c tel que:
\beta + \gamma = a^n\quad , \quad \gamma + \alpha = b^n \quad et \quad \alpha + \beta = c^n \;

2. bn + cn + (-a)n est un multiple de 2n + 1.

Z/(2n+1)Z est un corps dont le groupe multiplicatif est un groupe cyclique d'ordre 2n (cf groupe cyclique et anneau). En conséquence toute puissance de n d'un élément du groupe est d'ordre deux et est donc solution de l'équation X 2 - 1. Toute puissance de n d'un entier non multiple de 2n + 1 est donc congru à ±1 modulo 2n + 1. Les trois puissances α n, β n et γ n ne peuvent être en même temps congrus à ±1 car leur somme serait alors différente de zéro. Un au moins est donc multiple de 2n + 1. Comme 2n + 1 est un nombre premier, une puissance n'est multiple de 2n + 1 que si son facteur l'est aussi. Un des trois termes α, β ou γ est donc multiple de 2n + 1 car aucun n'est multiple de n, supposons que ce terme soit α. Le raisonnement s'applique de manière analogue dans le cas de β ou γ. En revanche deux facteurs ne peuvent en même temps être multiple de 2n + 1 car ils ne seraient plus premiers entre eux, β et γ sont donc congrus à ±1 modulo 2n + 1.
Il suffit alors de remarquer que bn + cn + (-a)n est égal à γ + α + α + β - (β + γ) = 2.α pour conclure que la somme est multiple de 2n + 1.

3. a est multiple de 2n + 1.

Si b est un multiple de 2n + 1, alors γ + α l'est aussi car γ + α = b n. Comme α est multiple de 2n + 1, il en est de même pour γ et ces deux entiers ne sont pas premiers entre eux, ce qui est contraire à l'hypothèse. Le raisonnement s'applique de la même manière pour c.
Le raisonnement du 2. montre que, comme bn + cn + (-a)n est congru à zéro modulo 2n + 1, un des trois termes est un multiple de 2n + 1. Comme ce n'est ni b ni c, a est un multiple de 2n + 1.

4. Les hypothèses initiales sont fausses et α.β.γ est un multiple de n.

Le raisonnement du 1. montre que β n-1 - β n-2.γ + ... + γ n-1 (respectivement α n-1 - α n-2.β + ... + β n-1) est une puissance de n. Il existe donc deux entiers u et v tel que :
u^n = \sum_{i=0}^{n-1} (-1)^i\beta^{n-1-i}\gamma^i \quad et \quad v^n= \sum_{i=0}^{n-1} (-1)^i\alpha^{n-1-i}\beta^i \;
Comme a est un multiple de 2n + 1, β est congru à -γ modulo 2n + 1. Un raisonnement analogue au 1. montre que n.β n-1 est congru à un modulo 2n + 1.
De plus, α est un multiple de 2n + 1, on en déduit que vn est congru à β n-1 modulo 2n + 1 et:
u^n \equiv n.\beta^{n-1} \quad et \quad v^n\equiv \beta^{n-1} \quad donc\quad u^n \equiv n.v^n \pmod {2n+1}\;
Dans Z/(2n+1)Z une puissance de n est égal soit à ±1 soit à 0. Les valeurs ±1 étant impossibles, u et v sont donc des multiples de 2n + 1. En conséquence β n-1 est aussi β est un multiple de 2n + 1 et α et β ne sont pas premiers entre eux, ce qui est contraire aux hypothèse.
En conclusion, il n'est pas possible de supposer que le triplet (α, β, γ) est une solution si α.β.γ n'est pas un multiple de n.

Cas où n est égal à cinq

Article détaillé : Entier de Dirichlet.
Dirichlet

Le théorème de Fermat est alors célèbre. Tous les efforts se concentrent sur le cas où le paramètre est égal à cinq. Sophie Germain a résolu le cas où aucune des inconnues n'est multiple de cinq. Cependant, malgré l'implication de nombreux membres de la communauté mathématique, plus de quinze ans s'écoulent sans progrès notable. En 1825 Dirichlet (1805 - 1859) devient immédiatement célèbre, pour un apport significatif. En général, un triplet solution, dans le cas où n est égal à cinq, contient un multiple de cinq et un multiple de deux. Dirichlet résolut le cas où les deux multiples sont associés à la même inconnue.

La démonstration est soumise à l'académie des sciences et Legendre est nommé référé. Il utilise les techniques de Dirichlet, et résout l'autre cas en quelques mois, c’est-à-dire celui où le multiple de deux et celui de cinq sont associés à des inconnues différentes[11].

Les deux démonstrations utilisent des techniques semblables à celle du cas où le paramètre est égal à trois. Elles se fondent sur l'arithmétique modulaire de l'anneau des entiers relatifs et d'un anneau d'entiers bien choisi. Cependant, cette fois-ci et à la différence du cas où n est égal à trois, l'extension cyclotomique associée, c’est-à-dire correspondant au corps de décomposition du polynôme cyclotomique n'est ni euclidien ni factoriel. Il devient nécessaire de considérer l'anneau des entiers du corps Q[√5] et non Q[i√5]. La structure, particulièrement le groupe des unités devient plus complexe. Sa compréhension revient à l'analyse d'une autre équation diophantienne dite de Pell-Fermat, étudiée par Euler. Les travaux de Lagrange sur les fractions continues fournissent les outils nécessaires à l'élucidation de cette structure. Cet anneau prend le nom d'anneau des entiers de Dirichlet, il permet d'établir le lemme clé de la démonstration.

À la différence des travaux de Gauss et d'Eisenstein sur le cas où n est égal à trois, aucune percée théorique majeure n'est réalisée pour la résolution de ce cas. L'anneau associé est toujours euclidien et donc factoriel, les arithmétiques utilisées sont de même nature que les précédentes.


Démonstration du cas n = 5

On suppose que (α, β, γ) est une solution non triviale telle que α, β et γ soient premiers entre eux dans leur ensemble et donc deux à deux.

Résolution du cas ou z est un multiple de cinq et de deux

L'équation s'écrit alors : x 5 + y 5 = 25.m.55.n.z' 5. Soit (α, β, γ') un triplet solution associée.

1. Il existe deux entiers p et q premiers entre eux, de parités opposées tel que α 5 + β 5 = 2p(p4 + 10p2q2 + 5q4 ).

γ est pair donc α et β sont impairs, α + β et α - β sont donc pairs et si p et q sont définis par 2p = α + β et 2q = α - β, alors α = p + q et β = p - q. De plus, p et q sont non nuls et premiers entre eux car α et β le sont. Alors un développement binomial montre que :
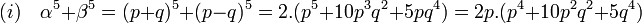
(i)\quad \alpha^5 + \beta^5 = (p + q)^5 + (p - q)^5 = 2.(p^5+10p^3q^2+5pq^4) = 2p.(p^4+10p^2q^2+5q^4)\;
Enfin, p et q sont de parités opposées car α et β sont impairs.

2. Il existe deux entiers q et r premiers entre eux de parités opposées tel que r soit multiple de cinq et α 5 + β 5 = 2.52.r(q4 + 50q2r2 + 125r4).

α 5 + β 5 est multiple de cinq, le terme 2p(p4 + 10p2q2 + 5q4 ) est donc multiple de cinq, ce qui montre que p l'est. Soit r l'entier défini par p = 5.r. En remplaçant p par 5.r dans l'équation (i), on obtient:
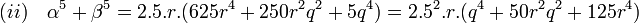
(ii)\quad \alpha^5 + \beta^5 = 2.5.r.(625r^4+250r^2q^2+5q^4)=2.5^2.r.(q^4+50r^2q^2+125r^4)\;
r est de même parité que p, chaque membre de l'équation (ii) est multiple de 55 donc soit r soit q est multiple de cinq. Or q est premier avec p et p est multiple de cinq, q n'est donc pas multiple de cinq et r l'est. Les notations suivantes sont alors utilisées:
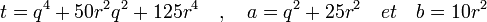
t=q^4+50r^2q^2+125r^4\quad , \quad a = q^2 + 25r^2 \quad et \quad b = 10r^2 \;

3. les entiers a et b sont deux entiers strictement positifs premiers entre eux de parités opposées et t = a2 - 5b2 est une puissance cinquième.

Un simple calcul montre que t = a2 - 5b2.
Montrons que a et b sont premiers entre eux. Soit f un diviseur de a et de b, f ne peut être pair car a est impair (q et r sont de parités différentes et a = q2 + 25r2). f ne peut être multiple de cinq car a n'est pas multiple de cinq (car q n'est pas multiple de cinq, en effet p et q sont premiers entre eux et p est un multiple de cinq). Enfin f est un diviseur de r car il divise b = 2.5.r2, comme il divise aussi a il est donc diviseur de q. Comme q et r sont premiers entre eux, f est égal à 1, ce qui montre que a et b sont premiers entre eux. Comme b est un multiple de deux et de cinq, a et b sont de parités différentes et a n'est pas un multiple de cinq.
Montrons que 2.52.r et t sont premiers entre eux. Soit f un diviseur des deux membres. Comme t est impair (t = a2 - 5b2 et a et b sont de parités opposées) f l'est aussi. Cinq divise p, donc il ne divise pas q. Si cinq ne divise pas q, il ne divise pas t ni f. Tout diviseur commun à r et t divise aussi q, donc r et t sont premiers entre eux. Donc, si f divise r, comme f divise r il est égal à un. Tout diviseur commun à 2.52.r et t est donc égal à un, et ils sont premiers entre eux.
L'égalité γ5 = 2.52.r.t permet de conclure que t et 2.52.r sont deux puissances cinquième car ils sont premiers entre eux. De plus q et r sont non nuls donc a et b sont des entiers strictement positifs.

4. Il existe deux entiers c et d, différents de zéro premiers entre eux de parités opposées tel que cinq divise d avec :

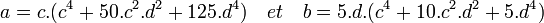
a=c.(c^4+50.c^2.d^2+125.d^4)\quad et \quad b=5.d.(c^4+10.c^2.d^2+5.d^4)\;
Ce passage correspond au lemme clé de la démonstration. Une fois prouvée, la suite est relativement mécanique. Comme pour le cas où le paramètre est égal à trois, le bon anneau d'entier est nécessaire. Ici, c'est l'anneau des entiers de Dirichlet. La démonstration est donnée dans le paragraphe Propriété associée aux entiers de Dirichlet pour la démonstration du dernier théorème de Fermat. L'unique élément à démontrer reste le fait que d est un multiple de cinq. Il suffit pour cela de remarquer que b est un multiple de 25, c n'est pas un multiple de cinq, donc d l'est. Utilisons alors les notations suivantes:
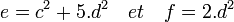
e=c^2 + 5.d^2 \quad et \quad f=2.d^2

5. e et f vérifient les hypothèse du lemme.

On remarque que e et f sont premiers entre eux. En effet, si θ est un diviseur commun à e et à f, alors θ ne divise pas 2 car c et d étant de parités différentes e est impair, θ est donc un diviseur de d et de c, il est donc égal à 1. On remarque de plus que f est pair et e impair, d est un multiple de cinq donc f l'est. Enfin, d est non nul donc f est aussi non nul, c n'est pas un multiple de cinq, donc e est aussi non nul.
Montrons que e 2 - 5.f 2 est une puissance cinquième. On remarque que:
e^2 -5.f^2=(c^2+5.d^2)^2-20.d^4=c^4+10.c^2.d^2+25.d^4-20.d^4=c^4+10.c^2.d^2+5.d^4 \;
Le terme correspond donc à un diviseur de b. L'égalité (ii) montre que 2.52.r est une puissance cinquième, il en est donc de même de son carré. Or :
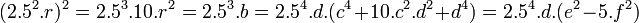
(2.5^2.r)^2=2.5^3.10.r^2=2.5^3.b=2.5^4.d.(c^4+10.c^2.d^2+d^4)=2.5^4.d.(e^2-5.f^2) \;
Il suffit donc de montrer que e 2 - 5.f 2 est premier avec 2, 5 et d pour prouver que c'est une puissance cinquième. La différence de parité entre e et f montre que l'expression est première avec 2. Comme e est premier avec 5 (car c l'est) l'expression est première avec 5. Enfin, c est premier avec d ce qui montre que l'expression, somme de c4 et de puissances de d, est première avec d. Les hypothèses du lemme sont bien vérifiées.
On en déduit l'existence de deux entiers g et h vérifiant les égalités suivantes et les conclusions du lemme :
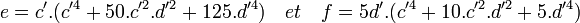
e=c'.(c'^4+50.c'^2.d'^2+125.d'^4)\quad et \quad f=5d'.(c'^4+10.c'^2.d'^2+5.d'^4)\;
Comme précédemment, nous utilisons les notations suivantes:
e' =c'^2 + 5.d'^2 \quad et \quad f' =2.d'^2

6. Existence d'une descente infinie.

e' et f' vérifient les hypothèses du lemme pour la même raison que pour le point 5. Le fait que l'expression e' 2 - 5.f' 2 soit une puissance cinquième provient du fait que 2.54.d est une puissance cinquièm et son carré aussi, donc :
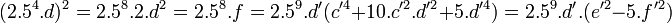
(2.5^4.d)^2=2.5^8.2.d^2=2.5^8.f=2.5^9.d'(c'^4+10.c'^2.d'^2+5.d'^4)=2.5^9.d'.(e'^2-5.f'^2) \;
Il suffit alors de montrer que l'expression est première avec 2, 5 et d' ce qui se montre comme précédemment. La suite d, d' etc... est une suite d'éléments non nuls, il suffit de montrer qu'elle est décroissante. Or la suite est strictement positive et entière, donc :
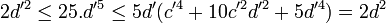
2d'^2 \le 25.d'^5 \le 5d'(c'^4+10c'^2d'^2+5d'^4)=2d^2
La suite génère une descente infinie, ce qui montre qu'une telle solution n'existe pas.

Voir aussi

Notes

  1. ↑ Tablette Plimpton 322 Université de Columbia -1900 - -1600
  2. ↑ Euclide Les quinze livres des éléments géométriques d'Euclide : plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant traduction de 1632, site Gallica
  3. ↑ R. Nogues Théorème de Fermat. Son histoire Paris, Librairie Vuibert 1932
  4. ↑ Cette information est corroborée par, par exemple le blog Site en anglais sur les démonstrations du Théorème de Fermat
  5. ↑ A. L. Cauchy Mémoire sur de nouvelles formules relatives à la théorie des polynômes radicaux, et sur le dernier théorème de Fermat Compte rendu de l'Académie t. XXIV, p. 516 1847]
  6. ↑ La démonstration proposée ici s'inspire du site : B. Edixhoven Cours de maîtrise de mathématiques : Théorie algébrique des nombres Université de Rennes 1 2002
  7. ↑ H. M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory Springer 3ème Ed 2000 (ISBN 0387950028)
  8. ↑ Leonhard Euler Algèbre 1770
  9. ↑ Tous les éléments amenant à une preuve sont réunis par Euler, même si la preuve n'est pas clairement rédigée, voir à ce sujet par exemple Le dernier théorème de Fermat par le site de l'Université de St Andrew
  10. ↑ Carl Friedrich Gauss Disquisitiones Arithmeticae 1801
  11. ↑ Dirichlet Démonstration du théorème de Fermat et de Wilson (compte-rendu par Cournot de quelques mémoires d'Abel, Jacobi et Lejeune-Dirichlet, au Journ. der Mathemat., de M. Crelle, t. 3, cah. 4). 1829, t. 11, p. 153-157

Liens externes

Références

  • Simon Singh, Le Dernier Théorème de Fermat, Poche, 2001.
  • P. Samuel, Théorie algébrique des nombres, Hermann, Paris, 1971.
  • A. Weil, Number theory, an approach through history, from Hammurapi to Legendre, Birkhäuser, 1983.
  • P. Ribenboim, 13 lectures on Fermat’s theorem, Springer Verlag, 1980.
  • P. Ribenboim, Fermat's Last Theorem for Amateurs Springer 2000 (ISBN 0387985085)
  • H.M. Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory Springer 3ième éd 2000 (ISBN 0387950028)
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « D%C3%A9monstrations du dernier th%C3%A9or%C3%A8me de Fermat ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Démonstration du dernier théorème de Fermat de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Dernier Théorème De Fermat — Travail de Diophante traduit du grec en latin par Claude Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre de Fermat écrivit que la… …   Wikipédia en Français

  • Dernier theoreme de Fermat — Dernier théorème de Fermat Travail de Diophante traduit du grec en latin par Claude Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre …   Wikipédia en Français

  • Dernier théorème de fermat — Travail de Diophante traduit du grec en latin par Claude Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre de Fermat écrivit que la… …   Wikipédia en Français

  • Demonstrations du dernier theoreme de Fermat — Démonstrations du dernier théorème de Fermat Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Démonstrations Du Dernier Théorème De Fermat — Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Démonstrations du dernier théorème de fermat — Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Démonstrations du dernier théorème de Fermat — Article principal : Dernier théorème de Fermat. En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z : Il stipule qu il… …   Wikipédia en Français

  • Dernier théorème de Fermat — En mathématiques, le dernier théorème de Fermat, ou théorème de Fermat Wiles, est un théorème de la théorie des nombres qui s énonce comme suit : Théorème   Il n existe pas de nombres entiers non nuls x, y et z tels que : dès… …   Wikipédia en Français

  • Démonstration du théorème de Fermat — Démonstrations du dernier théorème de Fermat Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Théorème de Fermat-Wiles — Dernier théorème de Fermat Travail de Diophante traduit du grec en latin par Claude Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”