Borne supérieure

Borne supérieure

Borne (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Borne.

Sommaire

Définition

Dans un ensemble ordonné E, la borne supérieure (resp. borne inférieure) d'une partie majorée (resp. minorée) F de E est, s'il existe, le plus petit (resp. le plus grand) majorant (resp. minorant) de F. Elle est classiquement notée sup(F) (resp. inf(F) ).

Une partie, même majorée, d'un ensemble ordonné ne possède pas nécessairement une borne supérieure ou inférieure.

Propriété de la borne supérieure

Un corps K possède la propriété de la borne supérieure si toute partie non vide et majorée de K possède une borne supérieure.

C'est notamment le cas du corps des réels.


\mathbb Q ne possède pas cette propriété

Il suffit de montrer qu'on peut trouver une partie de \mathbb Q qui ne possède pas de borne supérieure.

On considère le sous-ensemble : 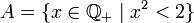A = \{x \in \mathbb Q _+ \;|\; x^2 < 2 \} et on montre que A ne possède pas de borne supérieure.

On remarque d'abord que tout rationnel b positif dont le carré est supérieur à 2 est un majorant de A car a² < 2 < b² conduit à a < b.

On suppose ensuite l'existence d'une borne supérieure b et on montre l'absurdité de cette supposition. Puisque 1 est élément de A, on sait que b est plus grand que 1. En comparant b² à 2, il n'existe que 3 possibilités

  1. b² = 2 (impossible car b est un rationnel et que √2 n'est pas rationnel)
  2. b² > 2
  3. b² < 2

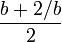
Pour montrer l'impossibilité du cas 2, il suffit d'exhiber,dans ce cas, un rationnel plus petit que b mais dont le carré est plus grand que 2, ce qui prouvera que b n'est pas le plus petit des majorants de A. La méthode de Héron permet d'exhiber ce rationnel : \frac{b+2/b}{2}

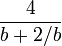
Pour montrer l'impossibilité du cas 3, il suffit d'exhiber, dans ce cas, un rationnel plus grand que b et dont le carré est plus petit que 2 ce qui prouvera que b n'est pas un majorant de A. Cette même méthode de Héron permet d'exhiber ce rationnel : \frac{4}{b+2/b}

Une borne supérieure de A aurait alors un carré qui ne serait ni inférieur à 2, ni supérieur à 2 ni égal à 2. Ce qui est absurde donc A ne possède pas de borne supérieure.

Exemples

  • Toute partie majorée non vide de l'ensemble des nombres réels possède une borne supérieure.
  • La borne supérieure de l'intervalle ]0,1[ est 1.
  • La borne inférieure de l'intervalle ]0,1[ est 0.
  • L'ensemble des nombres rationnels dont le carré est inférieur à 2 est une partie majorée de \mathbb Q qui n'a pas de borne supérieure dans \mathbb Q
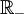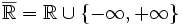  • La partie \mathbb R_- de \mathbb R ne possède pas de borne inférieure. Toutefois, considéré comme sous-ensemble de la droite achevée \overline{\mathbb R} = \mathbb R \cup \{-\infty,+\infty\} , il admet -\infty comme borne inférieure.
  • Un treillis est un ensemble ordonné où toute paire possède une borne supérieure et une borne inférieure.

Notions connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Borne (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Borne supérieure de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Theoreme de la borne superieure — Théorème de la borne supérieure Le théorème[1] de la borne supérieure dit que toute partie non vide majorée de l ensemble des nombres réels admet une borne supérieure. Note ↑ On l appelle parfois aussi axiome plutôt que théorème …   Wikipédia en Français

  • Théorème de la borne supérieure — Le théorème[1] de la borne supérieure dit que toute partie non vide majorée de l ensemble des nombres réels admet une borne supérieure. Note ↑ On l appelle parfois aussi axiome plutôt que théorème …   Wikipédia en Français

  • Borne (Mathématiques) — Pour les articles homonymes, voir Borne. Sommaire 1 Définition 2 Propriété de la borne supérieure 3 …   Wikipédia en Français

  • Borne inférieure — Borne (mathématiques) Pour les articles homonymes, voir Borne. Sommaire 1 Définition 2 Propriété de la borne supérieure 3 …   Wikipédia en Français

  • borne — [ bɔrn ] n. f. • v. 1180; bodne 1121; lat. pop. °bodina, p. ê. d o. gaul. 1 ♦ Pierre ou autre marque servant à délimiter un champ, une propriété foncière. ⇒ limite, terme. Borne témoin. Bornes d une parcelle. Planter, poser, déplacer une borne. 2 …   Encyclopédie Universelle

  • borné — borne [ bɔrn ] n. f. • v. 1180; bodne 1121; lat. pop. °bodina, p. ê. d o. gaul. 1 ♦ Pierre ou autre marque servant à délimiter un champ, une propriété foncière. ⇒ limite, terme. Borne témoin. Bornes d une parcelle. Planter, poser, déplacer une… …   Encyclopédie Universelle

  • Borne (mathématiques) — Pour les articles homonymes, voir Borne. En mathématiques, une borne est une extrémité d un intervalle dans lequel se situent tous les éléments d un ensemble donné ou toutes les valeurs d une fonction donnée. Une borne est un majorant si elle est …   Wikipédia en Français

  • Borne (Rivière) — Pour les articles homonymes, voir Borne. La Borne Caractéristiques …   Wikipédia en Français

  • Borne (riviere) — Borne (rivière) Pour les articles homonymes, voir Borne. La Borne Caractéristiques …   Wikipédia en Français

  • BORNE (É.) — Étienne BORNE 1907 1993 Né à Manduel (Gard) d’un père répétiteur au collège de Béziers, Étienne Borne entre en 1926 à l’École normale supérieure, où il connaît Raymond Aron, Jean Paul Sartre et Simone Weil, et fréquente le groupe “tala” de la rue …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”