Droite Projective

Droite projective

En géométrie, une droite projective est un espace projectif de dimension 1. Un espace vectoriel de dimension 2 y est associé.

Plus formellement, une droite projective sur un corps K, dénotée $\mathbb P ^1(K)$ peut être définie comme l'ensemble des sous-espaces à une dimension de l'espace vectoriel à deux dimensions K². On peut concevoir la droite projective comme la droite des K à laquelle on ajoute un point à l'infini.

La notion de droite projective se généralise pour les anneaux associatifs.

Coordonnées homogènes

En coordonnées homogènes, un point sur la droite projective $\mathbb P ^1(K)$ est une paire de la forme :

[x 1 : x 2]

où $x_1, x_2 \in K$ ne sont pas tous deux nuls. Deux telles paires sont dites égales si elles ne diffèrent que par un facteur non-nul λ :

[x 1 : x 2] = [λ x 1 :λ x 2].

La droite des K est identifiée au sous-ensemble de $\mathbb P ^1(K)$ donné par :

$\left\{[x : 1] \in \mathbb P^1(K) \big| x \in K\right\}.$

Ce sous-ensemble couvre tous les points dans K, excepté le point à l'infini

∞=[1:0].

Exemples

Nombres réels

Si le corps K est l'ensemble des nombres réels, alors la droite projective réelle est obtenue en projetant les point de ℝ² sur le cercle unitaire et en posant comme égaux les points diamétralement opposés. En termes de théorie des groupes, ceci équivaut à prendre le quotient avec le sous-groupe {1,-1}.

En termes de topologie, c'est un cercle. On peut le concevoir en imaginant les +∞ et -∞ des nombres réels collés ensemble pour ne former qu'un seul point à l'infini, ∞, dit point à l'infini dans la direction de la droite réelle. Le résultat est donc un cercle.

La droite projective réelle n'est pas équivalente à la droite réelle achevée, où une distinction est faite entre +∞ et -∞.

Nombres complexes

Si le corps K est l'ensemble des nombres complexes, alors l'ajout d'un point à l'infini au plan complexe ℂ² résulte en un espace qui, topologiquement, est une sphère. La droite projective complexe est aussi connue sous le nom de sphère de Riemann ou sphère de Gauss.

C'est l'exemple le plus simple de surface de Riemann. Ceci explique que la droite projective complexe est d'usage commun en analyse complexe, en géométrie algébrique et en théorie des variétés complexes.

Corps finis

Si le corps $K$ est fini et a q éléments, alors la droite projective a

q+1

éléments. On peut écrire tous ses sous-corps, sauf un, sous la forme :

y = ax

où 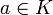$a \in K$ . Le cas restant est celui de la droite x=0.

Articles de Géométrie projective ou voisins à consulter.

[modifier]

Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques)

Portail de la géométrie

Ce document provient de « Droite projective ».

Catégorie : Géométrie projective

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Droite Projective de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Droite projective — En géométrie, une droite projective est un espace projectif de dimension 1. En première approche (en oubliant sa structure géométrique), la droite projective sur un corps K, notée , peut être définie comme l ensemble des droites vectorielles du… … Wikipédia en Français
Droite à l'infini — Dans le plan projectif, il est possible de définir un plan affine en choisissant une droite projective quelconque, que l on appelle alors droite à l infini associée à ce plan affine. Deux droites affines strictement parallèles correspondent à… … Wikipédia en Français
droite — [ drwat ] n. f. • XVIe; de droit I ♦ (de 2. droit) 1 ♦ Le côté droit, l aile, la partie droite. Il ne sait pas distinguer sa droite de sa gauche (⇒ latéralisé) . La droite d un navire. ⇒ tribord. Se coucher sur la droite. Se diriger vers la… … Encyclopédie Universelle
Droite (Mathématiques) — Pour les articles homonymes, voir Droite. Pour les Anciens, la droite, en mathématiques et surtout en géométrie, était un objet allant de soi, si évident que l on négligeait de préciser de quoi l on parlait. L un des premiers à formaliser la… … Wikipédia en Français
Droite (géométrie) — Droite (mathématiques) Pour les articles homonymes, voir Droite. Pour les Anciens, la droite, en mathématiques et surtout en géométrie, était un objet allant de soi, si évident que l on négligeait de préciser de quoi l on parlait. L un des… … Wikipédia en Français
Droite de Pascal — Théorème de Pascal Il existe plusieurs théorèmes appelés théorème de Pascal. Sommaire 1 Géométrie 1.1 Théorème de Pascal (direct et réciproque) 1.1.1 Théorème de Pappus Pascal … Wikipédia en Français
Droite (mathématiques) — Pour les articles homonymes, voir Droite. En géométrie, la droite désigne une ligne rectiligne, infinie et sans épaisseur. Dans la pratique, elle est représentée sur une feuille par une ligne droite ayant bien entendu des limites celle de la… … Wikipédia en Français
Geometrie projective — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques … Wikipédia en Français
Géométrie Projective — La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques 2 Aperçu élémentaire … Wikipédia en Français
Géométrie projective — En mathématiques, la géométrie projective est le domaine de la géométrie qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés inchangées des figures par projection. Sommaire 1 Considérations historiques 2… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Droite Projective