Compactifie d'Alexandroff
- Compactifie d'Alexandroff
-
Compactifié d'Alexandroff
Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère 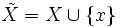 où
où 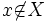 , et on définit une topologie de la manière suivante.
, et on définit une topologie de la manière suivante.
L'ensemble des ouverts de 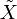 est constitué par :
est constitué par :
On vérifie alors que 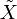 muni de cette topologie est un espace compact.
muni de cette topologie est un espace compact.
L'espace 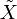 s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de
s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de 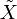 et se note également ∞.
et se note également ∞.
Exemples
Le compactifié d'Alexandroff de 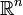 est homéomorphe à la sphère de dimension n.
est homéomorphe à la sphère de dimension n.
Par exemple le compactifié d'Alexandroff de  est un cercle, celui de
est un cercle, celui de 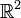 (ou
(ou  ) est une sphère, appelée communément sphère de Riemann.
) est une sphère, appelée communément sphère de Riemann.
Le point ajouté à l'espace peut être imaginé comme un point "à l'infini" : à l'infini la droite réelle se "referme" en un cercle.
Voir aussi
Compactification
 Portail des mathématiques
Portail des mathématiques
Catégories : Compacité | Théorème de mathématiques | Construction classique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Compactifie d'Alexandroff de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Compactifié d'Alexandroff — Soit un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à , obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante. L ensemble des ouverts de est … Wikipédia en Français
Compactifié d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… … Wikipédia en Français
Alexandroff — Aleksandrov Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronymes Aleksandrov, également Alexandrov ou Alexandroff (en russe : Александров), est un patronyme russe. Aleksandr Aleksandrov (1912 … Wikipédia en Français
Pavel Alexandroff — Pavel Aleksandrov Pour les articles homonymes, voir Aleksandrov. Pavel S. Aleksandrov. Pavel Sergueïevitch Aleksandrov (en russe … Wikipédia en Français
Compactification d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… … Wikipédia en Français
Théorème d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… … Wikipédia en Français
Compactification (mathématiques) — En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement implique que l espace doit être… … Wikipédia en Français
Compactification (Mathématiques) — En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement implique que l espace doit être… … Wikipédia en Français
Compactification (mathematiques) — Compactification (mathématiques) En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement… … Wikipédia en Français
Compactification de Stone–Čech — En mathématiques, et plus précisément en topologie générale, la compactification de Stone–Čech (découverte en 1937 par Marshall Stone (en)[1] et Eduard Čech[2]) est une technique de construction d un espace com … Wikipédia en Français
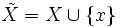 où
où 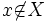 , et on définit une topologie de la manière suivante.
, et on définit une topologie de la manière suivante.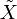 est constitué par :
est constitué par :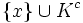 , où Kc est le complémentaire d'un compact K de X.
, où Kc est le complémentaire d'un compact K de X.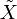 muni de cette topologie est un espace compact.
muni de cette topologie est un espace compact.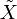 s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de
s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de 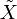 et se note également ∞.
et se note également ∞.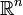 est homéomorphe à la sphère de dimension n.
est homéomorphe à la sphère de dimension n. est un cercle, celui de
est un cercle, celui de 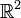 (ou
(ou  ) est une sphère, appelée communément sphère de Riemann.
) est une sphère, appelée communément sphère de Riemann.