Conditions de Karush-Kuhn-Tucker

Conditions de Kuhn-Tucker

Pour les articles homonymes, voir condition.

En mathématiques, les conditions de Kuhn-Tucker ou conditions de Karush-Kuhn-Tucker permettent de résoudre des problèmes d'optimisation sous contraintes non-linéaires d'inégalité.

Soient : 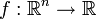$f: \mathbb{R}^n\to \mathbb{R}$ fonction pseudo-concave de n variables (fonction objective) et 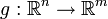$g: \mathbb{R}^n\to \mathbb{R}^m$ fonction quasi-concave (m représente le nombre de contraintes).

On note 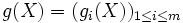$g(X)=(g_i(X))_{1 \le i \le m}$ : la fonction g résume les m contraintes $g i$ .

On suppose que la fonction f et les fonctions $g i$ admettent des dérivées partielles par rapport à chaque variable.

L'objectif est de trouver 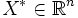$X^* \in \mathbb{R}^n$ qui maximise 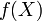$f(X) \,$ sous contrainte 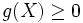$g(X) \ge 0$ , c'est-à-dire résoudre :

$X^*\in \arg \max_{X \in \mathbb{R}^n} f(X)$

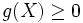sous contrainte $g(X) \ge 0$ .

Sommaire

1 Première étape : multiplicateurs de Lagrange
2 Deuxième étape : conditions de premier ordre
3 Troisième étape : conditions supplémentaires
- 3.1 Remarques
4 Théorème

Première étape : multiplicateurs de Lagrange

Soit 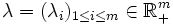$\lambda = (\lambda_i)_{1 \le i \le m} \in \mathbb{R}_+^m$ un vecteur de m nombres positifs (au sens large).

On appelle le Lagrangien la fonction :

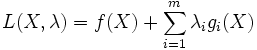$L(X, \lambda) = f(X) + \sum_{i=1}^m \lambda_i g_i(X)$ .

Les $λ i$ sont appelés multiplicateurs de Lagrange associés à la i-ième contrainte.

Deuxième étape : conditions de premier ordre

On considère L comme fonction objective d'un problème de maximisation (en fonction de X) sans contrainte. On écrit les conditions de premier ordre (conditions nécessaires) pour maximiser L en fonction de X :

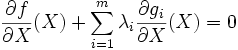$\frac{\partial f}{\partial X}(X) + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial X}(X)=0$ , où l'opérateur 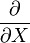$\frac{\partial}{\partial X}$ est le gradient.

Troisième étape : conditions supplémentaires

On écrit les conditions de relâchement supplémentaires ("complementary slackness conditions") et les conditions de positivité (conditions suffisantes) :

$\forall i \in \{1, ..., m\}, \min [\lambda_i, g_i(X)] = 0$ .

Remarques

la troisième étape implique que : 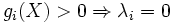$g_i(X)>0 \Rightarrow \lambda_i = 0$ : si la contrainte i n'est pas saturée, le multiplicateur de Lagrange associé à cette contrainte est nul ;

les conditions de premier ordre et les conditions de relâchement supplémentaires sont appelées conditions de Kuhn-Tucker.

Théorème

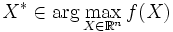
$X^*\in \arg \max_{X \in \mathbb{R}^n} f(X)$

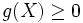
sous contrainte $g(X) \ge 0$

si et seulement si 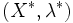$(X^*, \lambda^*) \,$ est solution des conditions de Kuhn-Tucker.

Articles en rapport avec la convexité
Géométrie convexe	Article principal : Ensemble convexe Outils et résultats fondamentaux : Enveloppe convexe • Adhérence, intérieur et frontière d'un convexe • Projection sur un convexe fermé • Séparation des convexes • Points remarquables à la frontière d'un convexe • Polytope • Théorème de Krein-Milman • Lemme de Farkas Géométrie combinatoire : Théorème de Carathéodory • Théorème de Radon • Théorème de Helly Géométrie métrique : Courbe de largeur constante • Théorème des quatre sommets Algorithmes de géométrie convexe : Approche polyèdrale • Marche de Jarvis • Parcours de Graham • Théorème optimisation/séparation Optimisation linéaire : Programmation linéaire • Algorithme du simplexe • Génération de colonnes
Interactions géométrie-analyse	Théorème de Hahn-Banach • Jauge
Analyse convexe	Article principal : Fonction convexe Outils et résultats fondamentaux : Inégalité de Jensen Optimisation convexe : Conditions de Kuhn-Tucker • Méthode du point intérieur
Utilisations de la convexité	Inégalités de convexité : Inégalité arithmético-géométrique • Inégalité de Hölder Analyse fonctionnelle : Espace localement convexe • Théorème du point fixe de Schauder Localisation de zéros de polynômes : Théorème de Gauss-Lucas Théorie des nombres : Théorème de Minkowski

Portail des mathématiques

Ce document provient de « Conditions de Kuhn-Tucker ».

Catégorie : Optimisation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conditions de Karush-Kuhn-Tucker de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Karush–Kuhn–Tucker conditions — In mathematics, the Karush–Kuhn–Tucker (KKT) conditions (also known as the Kuhn–Tucker conditions) are necessary for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied. Allowing inequality… … Wikipedia
Conditions De Kuhn-Tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français
Conditions de kuhn-tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français
Conditions de Kuhn-Tucker — Pour les articles homonymes, voir condition. En mathématiques, les conditions de Kuhn Tucker ou conditions de Karush Kuhn Tucker permettent de résoudre des problèmes d optimisation sous contraintes non linéaires d inégalité. Soient :… … Wikipédia en Français
Conditions d'optimalité (dimension finie) — En optimisation mathématique, les conditions d optimalité sont un ensemble d équations, d inéquations (i.e., des inégalités) et d expressions diverses (e.g., la semi définie positivité de matrices sur des cônes) vérifiées par une solution d un… … Wikipédia en Français
Albert William Tucker — Albert W. Tucker Albert William Tucker (28 novembre 1905 25 janvier 1995) était un mathématicien américain d origine canadienne qui a produit d importantes contributions en topologie, théorie des jeux et programmation non… … Wikipédia en Français
Albert W. Tucker — Albert William Tucker (28 novembre 1905 25 janvier 1995) était un mathématicien américain d origine canadienne qui a produit d importantes contributions en topologie, théorie des jeux et optimisation non linéaire. Biographie… … Wikipédia en Français
William Karush — Infobox Person name = William Karush caption = birth date = Birth date|1917|03|01 birth place = death date = Death date and age|1997|02|22|1917|03|01 death place = other names = known for = Contribution to Karush Kuhn Tucker conditions occupation … Wikipedia
Albert W. Tucker — Infobox Scientist name = Albert W. Tucker image width = 300px caption = Albert William Tucker birth date = birth date|1905|11|28|df=y birth place = Ontario, Canada death date = death date and age|1995|1|25|1905|11|28|df=y death place = Highstown … Wikipedia
Albert W. Tucker — Nacimiento 28 de noviembre de 1905 Ontario, Canadá Fallecimiento 25 de enero, 1995 Highstown, N.J., Estados Unidos Residencia … Wikipedia Español

Dictionnaires et Encyclopédies sur 'Academic'

Conditions de Karush-Kuhn-Tucker

Conditions de Kuhn-Tucker

Sommaire

Première étape : multiplicateurs de Lagrange

Deuxième étape : conditions de premier ordre

Troisième étape : conditions supplémentaires

Remarques

Théorème

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Conditions de Karush-Kuhn-Tucker

Conditions de Kuhn-Tucker

Sommaire

Première étape : multiplicateurs de Lagrange

Deuxième étape : conditions de premier ordre

Troisième étape : conditions supplémentaires

Remarques

Théorème

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link