- Optimisation (mathematiques)
-
Optimisation (mathématiques)
En mathématiques, l'optimisation est l’étude des problèmes qui sont de la forme :
- Étant donné : une fonction
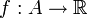 d’un ensemble A dans l'ensemble des nombre réels
d’un ensemble A dans l'ensemble des nombre réels - Rechercher : un élément x0 de A tel que
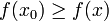 pour tous les x en A (« maximisation ») ou tel que
pour tous les x en A (« maximisation ») ou tel que 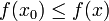 pour tous les x en A (« minimisation »).
pour tous les x en A (« minimisation »).
Une telle formulation est parfois appelée programme mathématique (terme non directement lié à la programmation informatique, mais utilisé par exemple pour la programmation linéaire - voir l’historique ci-dessous). Plusieurs problèmes théoriques et pratiques peuvent être étudiés dans cet encadrement général.
Étant donné que la maximisation de f est équivalente à la minimisation de − f, une méthode pour trouver le minimum (ou le maximum) suffit à résoudre le problème d'optimisation.
Il arrive fréquemment que A soit un sous-ensemble donné de l’espace euclidien
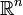 , souvent spécifié par un ensemble de contraintes, des égalités ou des inégalités que les éléments de A doivent satisfaire. Les éléments de A sont appelées les solutions admissibles et la fonction f est appelée la fonction objectif. Une solution possible qui maximise (ou minimise, si c’est le but) la fonction objectif est appelée une solution optimale. Dans le cas particulier où A est un sous-ensemble de
, souvent spécifié par un ensemble de contraintes, des égalités ou des inégalités que les éléments de A doivent satisfaire. Les éléments de A sont appelées les solutions admissibles et la fonction f est appelée la fonction objectif. Une solution possible qui maximise (ou minimise, si c’est le but) la fonction objectif est appelée une solution optimale. Dans le cas particulier où A est un sous-ensemble de 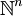 ou de
ou de 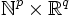 , on parle d'optimisation combinatoire.
, on parle d'optimisation combinatoire.Un minimum local x * est défini comme un point tel qu'il existe un voisinage V de x * tel que pour tout
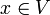 ,
, 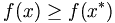 ; c’est-à-dire que dans une voisinage de x * toutes les valeurs de la fonction sont plus grandes que la valeur en ce point. Lorsque A est un sous-ensemble de
; c’est-à-dire que dans une voisinage de x * toutes les valeurs de la fonction sont plus grandes que la valeur en ce point. Lorsque A est un sous-ensemble de 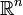 , ou plus généralement un espace vectoriel normé, cela s'écrit : pour un δ > 0 donné et tous les x tels que
, ou plus généralement un espace vectoriel normé, cela s'écrit : pour un δ > 0 donné et tous les x tels que 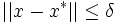 on a
on a 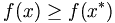 . Les maximums locaux sont définis semblablement. En général, il est facile de trouver les minimums (maximums) locaux, qui sont parfois nombreux. Pour vérifier que la solution trouvée est un minimum (maximum) global, il est nécessaire de recourir à des connaissances additionnelles sur le problème (par exemple la convexité de la fonction objectif).
. Les maximums locaux sont définis semblablement. En général, il est facile de trouver les minimums (maximums) locaux, qui sont parfois nombreux. Pour vérifier que la solution trouvée est un minimum (maximum) global, il est nécessaire de recourir à des connaissances additionnelles sur le problème (par exemple la convexité de la fonction objectif).Sommaire
Notation
Les problèmes d’optimisation sont souvent exprimés avec une notation spéciale. Voici quelques exemples :
On cherche la valeur minimale pour l’expression x2 + 1, où x s’étend sur les nombres réels
 . La valeur minimale dans ce cas est 1, s’occasionnant à x = 0.
. La valeur minimale dans ce cas est 1, s’occasionnant à x = 0.On cherche la valeur maximale pour l’expression 2x, où x s’étend sur les réels. Dans ce cas, il n’y a pas de tel maximum puisque l’expression n’est pas bornée, donc la réponse est « l’infini » ou « indéfini ».
On cherche la ou les valeurs de x dans l'intervalle
![]-\infty, -1]](/pictures/frwiki/49/1d6ab33b3fb95d1dab60c3aea17122a8.png) qui minimise l'expression x2 + 1. (La valeur minimale véritable de cette expression n'est pas importante.) Dans ce cas, la réponse est x = − 1.
qui minimise l'expression x2 + 1. (La valeur minimale véritable de cette expression n'est pas importante.) Dans ce cas, la réponse est x = − 1.On cherche la ou les paires (x,y) qui maximisent la valeur de l'expression xcos(y), avec la contrainte ajoutée que la valeur absolue de x ne peut excéder 5. (À nouveau, la valeur maximale véritable de l'expression n'est pas importante.) Dans ce cas, les solutions sont les paires de la forme (5,2kπ) et ( − 5,(2k + 1)π), où k s'étend sur tous les entiers.
Techniques
Les techniques pour résoudre les problèmes mathématiques dépendent de la nature de la fonction objectif de l'ensemble contraint. Les sous-domaines majeurs suivants existent :
- la programmation linéaire étudie les cas où la frontière de l’ensemble A et la fonction objectif sont linéaires. C’est une méthode très employée pour établir les programmes des raffineries pétrolières, mais aussi pour déterminer la composition la plus rentable d’un mélange salé, sous contraintes, à partir des prix de marché du moment.
- la programmation linéaire en nombres entiers étudie les programmes linéaires dans lesquels certaines ou toutes les variables sont contraintes à prendre des valeurs entières. Ces problèmes peuvent être résolus par différentes méthodes: séparation et évaluation, plans sécants.
- la programmation quadratique permet à la fonction objectif d’avoir des termes quadratiques, tout en conservant une description de l’ensemble A à partir d'égalités/inégalités linéaires
- la programmation non-linéaire étudie le cas général dans lequel l’objectif ou les contraintes (ou les deux) contiennent des parties non-linéaires
- la programmation stochastique étudie le cas dans lequel certaines des contraintes dépendent de variables aléatoires
- la programmation dynamique utilise la propriété qu’une solution optimale se compose nécessairement de sous-solutions optimales (attention : le contraire n'est pas vrai en général) pour décomposer le problème en évitant l’explosion combinatoire. Elle n’est utilisable que lorsque la fonction objectif est monotone croissante. C’est la programmation dynamique qui permet par exemple
- aux avionneurs de trouver les plans de décollage optimaux de leurs engins,
- aux ingénieurs de bassin de répartir la production minière entre leurs différents puits
- aux media planners de répartir efficacement un budget de publicité entre différents supports
Pour les fonctions dérivables deux fois, des problèmes sans contraintes peuvent être résolus en trouvant les lieux où le gradient de la fonction est 0 (par exemple les points stationnaires) et en utilisant la matrice hessienne pour classer le type de point. Si le hessien est défini positif, le point est un minimum local ; s’il est un défini négatif, un maximum local et s’il est indéfini c’est un « point-col ».
Si la fonction est convexe sur l’ensemble des solutions admissibles (définies par les contraintes) alors tout minimum local est aussi un minimum global. Des techniques numériques robustes et rapides existent pour optimiser des fonctions convexes doublement dérivables. En dehors de ces fonctions, des techniques moins efficaces doivent être employées.
Les problèmes à contraintes peuvent souvent être transformés en des problèmes sans contraintes à l’aide du multiplicateur de Lagrange : cette méthode revient en effet à introduire des pénalités croissantes à mesure qu’on se rapproche des contraintes. Un algorithme dû à Hugh Everett permet de mettre à jour de façon cohérente les valeurs des multiplicateurs à chaque itération pour garantir la convergence. Celui-ci a également généralisé l'interprétation de ces multiplicateurs pour les appliquer à des fonctions qui ne sont ni continues, ni dérivables. Le lambda devient alors juste un coefficient de pénalité.
De nombreuses techniques existent pour trouver un bon minimum local dans les problèmes d’optimisation non-linéaires avec plusieurs minimums locaux pauvres, elles sont généralement considérées comme des métaheuristiques.
Utilisations
Les problèmes de la dynamique à corps rigides (surtout la dynamique des corps rigides articulée) ont souvent besoin de techniques de programmation mathématique, puisqu'on peut voir la dynamique des corps rigides comme résolution d'une équation différentielle ordinaire sur une variété contrainte ; les contraintes sont diverses contraintes géométriques non-linéaires telles que « ces deux points doivent toujours coïncider », ou « ce point doit toujours être sur cette courbe ». Aussi, le problème de calculer les forces de contact peut être achevé en résolvant un problème de complémentarité linéaire, qui peut aussi être vu comme un PPQ (problème de programmation quadratique).
Plusieurs problèmes de conception peuvent aussi être exprimés sous forme de programmes d’optimisation. Cette application est appelée l’optimisation de forme. Un sous-ensemble récent et croissant de ce domaine s’appelle l’Optimisation multidisciplinaire qui, bien qu’utile en plusieurs problèmes, a été particulièrement appliqué aux problèmes du génie aérospatial.
Un autre domaine qui utilise les techniques de l’optimisation est la recherche opérationnelle.
L’optimisation est un des outils centraux de la microéconomie qui est basée sur le principe de la rationalité et de l’optimisation des comportements, le profit pour les entreprises, et l’utilité pour les consommateurs.
En mécanique on distingue trois formes d'optimisation[1] :
- l'optimisation de taille ou optimisation paramétrique, qui consiste à optimiser des dimensions (longueur, épaisseur, diamètre, ...) de la structure mécanique ;
- l'optimisation de forme, qui consiste à optimiser l'enveloppe d'une pièce sans changer la topologie, c'est-à-dire sans ajouter de trous dans la pièce ;
- l'optimisation topologique, qui consiste à faire varier la répartition de matière au sein d'un volume de départ donné.
Historique
Historiquement, le premier terme introduit fut celui de programmation linéaire, inventé par George Dantzig dans les années 1940. Le terme programmation dans ce contexte ne réfère pas à la programmation informatique (bien que les ordinateurs soient largement utilisés de nos jours pour résoudre des programmes mathématiques). Il vient de l’usage du mot programme par les forces armées américaines pour établir des horaires de formation et des choix logistiques, que Dantzig étudiait à l’époque. L’emploi du terme « programmation » avait également un intérêt pour débloquer des crédits en une époque où la planification devenait une priorité des gouvernements.
Notes et références
- ↑ Catherine Vayssade, « Optimisation mécanique, Optimisation topologique », 2004. Consulté le 24 décembre 2008
Voir aussi
Articles connexes
- Descente de gradient
- Algorithme du simplexe
- Théorie des jeux,
- Les compilateurs pour les langages de programmation,
- Recherche opérationnelle,
- Logique floue,
- Optimisation aléatoire,
- Hugh Everett
- Métaheuristique,
- Inégalité de variation,
- Complémentarité mixte,
- Algorithme simple
- Microéconomie
- Relaxation Dynamique
- Fonction objectif.
Bibliographie
- (fr) Michel Minoux, Programmation mathématique - théorie et algorithmes, éditions Dunod, 1983 (ISBN 2040154876)
- (en) Encyclopedia of Optimization, Floudas, Christodoulos A.; Pardalos, Panos M. (éditeurs), 2e édition, 2009 (ISBN 978-0-387-74758-3)
Liens externes
- (en) Guide NEOS
- Portail des mathématiques
Catégorie : Optimisation - Étant donné : une fonction
Wikimedia Foundation. 2010.

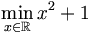
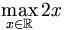
![\arg \min_{x \in ]-\infty, -1]} x^2 + 1](/pictures/frwiki/98/b58195f0dd0ec89a6fcc2e54c1c249c9.png)
![\arg \max_{x \in [-5, 5], y \in \mathbb{R}} x \cos(y)](/pictures/frwiki/52/4881cbe7eef923ce6d71a8afc4f3abaf.png)