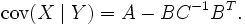- Complément de schur
-
Complément de Schur
En algèbre linéaire et plus précisément en théorie des matrices, le complément de Schur est défini comme suit. Soit
une matrice de dimension (p+q)×(p+q), où les blocs A, B, C, D sont des matrices de dimensions respectives p×p, p×q, q×p and q×q, avec D inversible. Alors, le complément de Schur du bloc D de la matrice M est constitué par la matrice de dimension p×p suivante :
- A − BD − 1C.
Lorsque B est la transposée de C, la matrice M est symétrique définie-positive si et seulement si D et son complément de Schur dans M le sont.
Le complément de Schur apparaît en particulier comme le résultat d'une élimination de Gauss «partielle» en multipliant la matrice M à droite avec la matrice «triangulaire inférieure» par blocs suivante
Ici, Ip désigne la matrice identité de dimension p×p. Après multiplication par la matrice LT, le complément de Schur apparaît dans le bloc p×p supérieur. La matrice produit est
L'inverse de M peut ainsi être exprimée en termes de D − 1 et de l'inverse du complément de Schur
ou encore plus simplement,
Application à la résolution d'équations linéaires
Le complément de Schur apparaît naturellement lors de la résolution d'un système d'équations linéaires de la forme
- Ax + By = a
- Cx + Dy = b
où
- x et a sont des vecteurs colonne de dimension p,
- y et b sont des vecteurs colonne de dimension q,
- A, B, C, D sont comme précédemment.
En multipliant la seconde équation par BD − 1 puis en la soustrayant de la première, il vient
Ainsi, la résolution de cette équation en x est possible dès que D et son complément de Schur sont inversibles. Il est ensuite possible d'obtenir y en résolvant l'équation Cx + Dy = b. Cette méthode réduit le problème de l'inversion d'une matrice de dimension
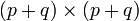 à celui de l'inversion de deux matrices de dimensions respectives p×p et q×q. En pratique, la matrice D doit être bien conditionnée pour rendre la méthode précise.
à celui de l'inversion de deux matrices de dimensions respectives p×p et q×q. En pratique, la matrice D doit être bien conditionnée pour rendre la méthode précise.Applications aux probabilités et à la statistique
Soit (X,Y) un vecteur gaussien de Rn+m de matrice de covariance
Ici, X (respectivement Y) est un vecteur gaussien de Rn (respectivement Rm) de matrice de covariance A (respectivement C).
La loi conditionnelle de X sachant Y est encore une loi gaussienne multivariée de dimension n. Supposons que la matrice V est inversible (elle est donc symétrique et définie positive). Alors, la matrice de covariance de la loi conditionnelle de X sachant Y ne dépend pas de Y et est donnée par le complément de Schur de C dans V.
Cela montre en particulier que le complément de Schur d'un bloc diagonal d'une matrice de covariance empirique d'un échantillon gaussien suit une loi de Wishart (tout comme la matrice de covariance empirique elle-même).
Bibliographie
- Chapitre 7 du livre de R. A. Horn et C. R. Johnson, intitulé « Matrix Analysis », plusieurs fois édité par Cambridge University Press.
- Portail des mathématiques
Catégories : Matrice | Probabilités | Statistiques
Wikimedia Foundation. 2010.

![M=\left[\begin{matrix} A & B \\ C & D \end{matrix}\right]](/pictures/frwiki/54/66eb0aebf60bfc9e21dabb25f1e399fe.png)
![LT=\left[\begin{matrix} I_p & 0 \\ -D^{-1}C & D^{-1} \end{matrix}\right].](/pictures/frwiki/51/342b2b8f5f6da1c37142e6cb3341219b.png)
![M\cdot LT=\left[\begin{matrix} A-BD^{-1}C & BD^{-1} \\ 0 & I_q \end{matrix}\right].](/pictures/frwiki/52/4e6da9f21853f5477f423f71d9ffa67a.png)
![\left[ \begin{matrix} A & B \\ C & D \end{matrix}\right]^{-1} = \left[ \begin{matrix} \left(A-B D^{-1} C \right)^{-1} & -\left(A-B D^{-1} C \right)^{-1} B D^{-1} \\ -D^{-1}C\left(A-B D^{-1} C \right)^{-1} & D^{-1}+ D^{-1} C \left(A-B D^{-1} C \right)^{-1} B D^{-1} \end{matrix} \right],](/pictures/frwiki/48/0d2c2e0174616f640392b080c9e830d3.png)
![\left[ \begin{matrix} A & B \\ C & D \end{matrix}\right]^{-1} =
\left[ \begin{matrix} I & 0 \\ -D^{-1}C & I \end{matrix}\right]
\left[ \begin{matrix} (A-BD^{-1}C)^{-1} & 0 \\ 0 & D^{-1} \end{matrix}\right]
\left[ \begin{matrix} I & -BD^{-1} \\ 0 & I \end{matrix}\right].](/pictures/frwiki/48/07262de61e448bcdcd9fb0c691f2b5a6.png)
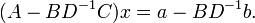
![V=\operatorname{cov}(X,Y)=\left[\begin{matrix} A & B \\ B^T & C \end{matrix}\right].](/pictures/frwiki/101/eccca9e6360388294ec6cc63539a925f.png)