Compacité (mathématiques)

Pour les articles homonymes, voir Compacité et Compact.

En topologie, on dit d'un espace séparé qu'il est compact, ou qu'il vérifie la propriété de Borel-Lebesgue, si chaque fois qu'il est recouvert par des ouverts, il est recouvert par un nombre fini d'entre eux. La condition de séparation est parfois omise et certains résultats demeurent vrais, comme le théorème des bornes généralisé, ou le théorème de Tychonov. Le nom choisi pour cette propriété rend hommage aux mathématiciens français Émile Borel et Henri Lebesgue, car le théorème qui porte leur nom établit que tout segment de la droite réelle est compact, et plus généralement, que les compacts de ℝⁿ sont les fermés bornés. Une approche plus intuitive de la compacité dans le cas particulier des espaces métriques est détaillée dans l'article Compacité séquentielle.

Propriété de Borel-Lebesgue

Définition préalable : Soit E un ensemble et A une partie de E. On dit qu'une famille (U_i)_i∊I de parties de E recouvre A si sa réunion ∪_i∊IU_i contient A.

Propriété de Borel-Lebesgue pour les segments : soit un segment [a,b] de la droite réelle. De tout recouvrement ouvert de ce segment, on peut extraire un sous-recouvrement fini. C'est-à-dire que pour toute famille (U_i)_i∊I d'ensembles ouverts recouvrant [a,b], il existe une partie finie J de I telle que la sous-famille (U_i)_i∊I recouvre déjà [a,b].

Pour une démonstration de cette propriété voir le théorème de Borel-Lebesgue, aussi appelé théorème de Heine-Borel.

La propriété de Borel-Lebesgue est étroitement liée à une propriété des suites bornées de réels : de toute suite bornée de réels, on peut extraire une suite convergente. Le lien entre les deux propriétés est explicité plus bas (dans la section « Théorème de Bolzano-Weierstrass et compacité séquentielle »).

De l'une ou l'autre de ces propriétés il est possible de tirer quelques conséquences importantes sur les fonctions numériques. Notamment : l'image d'un segment par une application continue est non seulement (d'après le théorème des valeurs intermédiaires) un intervalle, mais c'est même un segment (théorème des bornes), et la fonction est alors uniformément continue (théorème de Heine).

La propriété de Borel-Lebesgue (de même que la compacité séquentielle) peut se formuler comme une propriété intrinsèque de l'espace topologique étudié (ici : l'espace [a,b] muni de sa topologie usuelle), indépendamment du fait que celui-ci soit, éventuellement, inclus dans un espace topologique « plus gros » (ici : ℝ), et soit muni de ce fait de la topologie induite. En ce sens, la notion de « partie compacte » (d'un espace topologique) diffère fondamentalement de celle, par exemple, de « partie fermée ».

Axiome de Borel-Lebesgue et définition générale des compacts

Un espace topologique E est dit quasi-compact s'il vérifie l'axiome de Borel-Lebesgue : de tout recouvrement ouvert de E, on peut extraire un sous-recouvrement fini. L'espace est dit compact quand il est en outre séparé au sens de Hausdorff (T2).

Par passage aux complémentaires, la propriété de Borel-Lebesgue équivaut à : si (F_i)_i∊I est une famille de fermés telle que ∩_i∊I F_i=∅, alors on peut extraire une famille finie (F_i)_i∊J, avec J⊂I, telle que ∩_i∊J F_i=∅. Ou encore, par contraposition, si toute intersection finie ∩_i∊J F_i d'une famille de fermés est non vide, alors l'intersection ∩_i∊I F_i de toute la famille est non vide.

NB : En terminologie anglo-saxonne, la définition est légèrement différente. Sauf mention contraire, le compact anglophone est un quasi-compact francophone, et la notion de quasi-compacité n'existe pas. Toutes les propriétés ne s'appliquent donc pas en général, sauf sous l'hypothèse que l'espace est séparé.

Définition par la théorie des filtres

Un espace topologique séparé est compact si et seulement si pour tout filtre F sur E, il existe un filtre plus fin que F qui converge, ou encore si et seulement si tout ultrafiltre sur E converge. Cette définition équivalente est rarement utilisée. Elle est particulièrement adéquate pour prouver que tout produit de compacts est compact.

Exemples

• Tout espace fini est quasi-compact puisqu'il n'a qu'un nombre fini d'ouverts.
• Dans un espace séparé, étant donnée une suite convergente, l'ensemble constitué des termes de la suite ainsi que de la limite est compact. En effet, de tout recouvrement ouvert, on peut extraire un ouvert contenant la limite ; comme il n'existe qu'un nombre fini de termes hors de cet ouvert, il est aisé de trouver un sous-recouvrement fini.
• Tout ensemble muni de la topologie cofinie est quasi-compact.

Propriétés

Compacts et fermés

Dans un espace séparé, deux parties compactes disjointes sont toujours incluses dans deux ouverts disjoints.

Toute partie compacte d'un espace séparé est fermée.

• Preuve : soit A une partie compacte d'un espace séparé E. Montrons que son complémentaire B est ouvert. Pour tout point b de B, d'après la propriété précédente, il existe un ouvert W contenant b et disjoint d'un ouvert contenant A. Un tel W est a fortiori disjoint de A donc inclus dans B. Par conséquent B est voisinage de tous ses points, donc ouvert.

• NB : Ceci est en général faux si l'espace ambiant n'est pas séparé ; par exemple dans ℝ muni de la topologie grossière, {1} est compact mais pas fermé.

Toute partie fermée d'un espace compact est compacte.

Preuve : montrons que plus généralement, toute partie fermée d'un espace quasi-compact est quasi-compacte, pour la topologie induite (l'énoncé ci-dessus s'en déduit en remarquant que toute partie d'un espace séparé est encore séparée). Soient C un espace quasi-compact et F une partie fermée de C. Montrons que F vérifie la propriété de Borel-Lebesgue formulée en termes de fermés. Soit (F_i ) une famille de fermés de F dont toute intersection finie est non vide. Comme les F_i sont aussi des fermés du compact C, leur intersection est non vide, ce qui conclut.

Un espace compact est normal.

Preuve : dans un espace compact E, soient A, B deux fermés disjoints. D'après les propriétés ci-dessus, A et B sont alors deux compacts disjoints et E est séparé, si bien que A et B sont inclus dans deux ouverts disjoints, ce qui prouve que E est normal.

Autres propriétés

Les compacts de l'ensemble des nombres réels, muni de sa topologie usuelle, sont les fermés bornés.

Ce résultat est connu sous le nom de théorème de Borel-Lebesgue.

Le produit cartésien de compacts, munis de la topologie produit est compact.

Ce résultat est connu sous le nom de théorème de Tychonov.

Dans un espace vectoriel normé réel de dimension finie^[1], les compacts sont les fermés bornés.

En effet, par équivalence des normes, cet énoncé se ramène à la caractérisation des compacts de ℝⁿ, fournie par le théorème de Borel-Lebesgue. (Il existe même une généralisation aux espaces vectoriels topologiques de dimension finie.) Le caractère fini de la dimension est primordial. On démontre en effet que la boule unité centrée en 0 et de rayon 1 n'est pas compacte dans un espace vectoriel normé de dimension infinie. Ce résultat est un théorème de Riesz.

Toute partie discrète d'un compact est finie.

Un espace séparé X est compact si et seulement si pour tout espace Y, la projection p_Y : X×Y → Y est une application fermée.

Plus généralement, un espace X est quasi-compact si et seulement s'il vérifie cette propriété^[2].

Compacité et continuité

Une fonction à valeurs réelles continue sur un compact atteint toujours son maximum.

L'image d'un compact, par une application continue à valeurs dans un espace séparé, est compacte.

Montrons que plus généralement, l'image d'un quasi-compact C⊂X par une application continue f : X → Y (avec Y non nécessairement séparé) est quasi-compacte. Soit g : C → f(C) la restriction-corestriction (continue) de f. Considérons un recouvrement ouvert de f(C), son image réciproque par g est un recouvrement ouvert de C. On peut en extraire un sous-recouvrement fini. Par surjectivité de g, l'image par g de ce sous-recouvrement est un sous-recouvrement de f(C) extrait du recouvrement initial. L'existence d'un tel sous-recouvrement démontre la quasi-compacité de f(C).

Un premier exemple d'usage de ce résultat est le théorème des bornes (ou théorème de Weierstrass), stipulant que l'image d'un segment par une application continue de ℝ dans ℝ atteint ses bornes.

Un deuxième exemple est la démonstration du caractère isopérimétrique d'un polygone régulier, question ouverte depuis l'antiquité. L'objet est de savoir quel est le polygone à n côtés qui possède la plus grande aire, pour un périmètre donné. Des raisonnements géométriques assez simples montrent que l'unique candidat possible est le polygone régulier, résultat démontré depuis l'antiquité grecque. En revanche, l'existence d'une solution à cette question est restée ouverte jusqu'au XIX^e siècle.

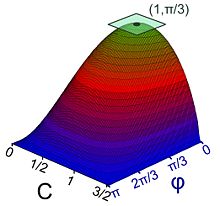
Pour comprendre la nature de la démonstration, le plus simple est de considérer le cas du triangle, illustré sur la figure de droite. Les triangles considérés sont tous de périmètre 3, ils sont identifiés à un couple (c, φ) où c désigne la longueur d'un côté et φ l'angle entre deux côtés dont l'un est celui de longueur c. La fonction f est celle qui, à un couple, associe la surface du triangle. Il n'est nécessaire que d'étudier la zone où c est compris entre 0 et ³⁄₂ et φ entre 0 et π. Cette zone est un compact de ℝ². L'application f est continue, elle atteint donc son maximum, en l'occurrence au point (1, ^π⁄₃). L'existence de ce maximum était le chaînon manquant pour une démonstration complète.

Pour le triangle, un peu d'analyse permet tout aussi bien de démontrer le résultat. Pour le cas général du polygone à n côtés, il n'est pas bien difficile de construire une démonstration analogue à celle présentée ici, grâce à la notion de compact. La solution analytique est en revanche vraiment lourde. Une démonstration détaillée est présentée dans l'article théorème isopérimétrique.

Un corollaire du théorème sur l'image continue d'un compact est :

Toute application continue d'un espace compact dans un espace séparé est fermée. En particulier, si elle est bijective alors c'est un homéomorphisme.

Théorème de Bolzano-Weierstrass et compacité séquentielle

Lorsque K est un espace métrique (automatiquement séparé), le théorème de Bolzano-Weierstrass énonce que K est compact si et seulement si de toute suite d'éléments de K il est possible d'extraire une sous-suite qui converge vers un élément de K, ou, de manière équivalente, toute suite admet une valeur d'adhérence.

Pour cette raison, dans le cadre des espaces métriques, la propriété de compacité est fréquemment introduite par caractérisation séquentielle.

Notes et références

• N. Bourbaki, Éléments de mathématique. Livre III : Topologie générale, [détail des éditions], chapitre I
• Georges Skandalis, Topologie et analyse 3^e année, Dunod, coll. « Sciences Sup », 2001
• Claude Wagschal, Topologie et analyse fonctionnelle, Hermann, coll. « Méthodes », 1995

• Portail des mathématiques