Valeur d'adherence

Valeur d'adhérence

En topologie, si $(u_n)_{n\in\mathbf{N}}$ est une suite à valeurs dans un ensemble $E$ , une valeur d'adhérence de la suite $(u n)$ est un point de $E$ près duquel s'accumulent une infinité de termes de la suite. Pour donner un sens mathématique à cela, il faut pouvoir mesurer la proximité, ce qui nécessite de munir $E$ d'une topologie. La notion de valeur d'adhérence dépend alors de la topologie choisie. Dans un espace où tout point admet une base dénombrable de voisinages (c'est le cas notamment dans un espace métrique) les valeurs d'adhérences d'une suite sont les limites de ses sous-suites. Cette dernière propriété est souvent prise comme définition d'une valeur d'adhérence, mais n'est cependant pas équivalente à la définition la plus générale.

Valeurs d'adhérence de suites réelles

Les propriétés topologiques de $\mathbf{R}$ (notamment le fait qu'il soit métrique et complet) impliquent des propriétés intéressantes de l'ensemble des valeurs d'adhérence des suites réelles.

Définition et caractérisation

Soient $(u_n)_{n\in\mathbf{N}}$ une suite réelle et $a$ un nombre réel, on dit que $a$ est une valeur d'adhérence de $(u n)$ s'il existe une sous-suite de $(u n)$ noté $(u_{\varphi(n)})$ qui converge vers $a$ .

Ceci est équivalent aux deux propriétés suivantes :

$(\forall \varepsilon\in\mathbb{R}_{+}^{*})(\forall N\in\mathbb{N}) (\exist n>N, \;|u_n-a|<\varepsilon)$ $(\forall \varepsilon\in\mathbb{R}_{+}^{*})$ l'ensemble $\left \{u_n,\; |u_n-a|<\varepsilon\right \}$ est infini

La deuxième propriété n'est qu'une caractérisation ensembliste de la première. Pour montrer l'équivalence avec la définition, il suffit de remarquer que le $ε$ peut être aussi petit que l'on veut, ce qui permet de trouver une sous-suite qui converge vers $a$ . Plus précisément, on la démonstration suivante :

Démonstration

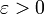On suppose que $(u_{\varphi(n)})$ converge vers $a$ . Soit alors $\varepsilon >0$ , et $N\in\mathbf{N}$ . La définition de la convergence nous fournit un entier $N 0$ tel que :

$(\forall n\geq N_0)(|u_{\varphi(n)}-a|<\varepsilon)$

On peut donc trouver un entier $n 0$ plus grand que $N$ et $N 0$ tel que $|u_{\varphi(n_0)}-a|<\varepsilon$
Mais alors vu que $\varphi(n_0)>n_0$ , l'entier $\varphi(n_0)$ est également plus grand que $N$ et $N 0$ et vérifie donc la propriété.

Réciproquement, considérons une suite vérifiant la propriété. On veut trouver une sous-suite de $(u n)$ qui converge vers $a$ . En prenant par exemple $\varepsilon=\frac{1}{n}$ dans la propriété, on construit par récurrence une extraction 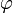$\varphi$ telle que la sous-suite $(u_{\varphi(n)})$ vérifie la propriété suivante :

$(\forall n\in\mathbf{N})\left(|u_{\varphi(n)}-a|<\frac{1}{n}\right)$

Pour

n = 1

, il existe

n 0 > 1

tel que $|u_{n_0}-a|<1$ . On note $\varphi(1)$ un tel entier.

Supposons 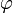$\varphi$ définie jusqu'au rang

n

, la propriété nous fournit au moins un entier

n 0

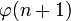avec $n_0\geq\sup(n+1,\varphi(1),\varphi(2),\ldots,\varphi(n))$ tel que $|u_{n_0}-a|<\frac{1}{n}$ . On peut alors noter $\varphi(n+1)$ un tel entier.

Il est maintenant clair que la suite ainsi construite converge vers $a$ , ce qui achève la démonstration.

Exemples

la suite $(( - 1) n)$ admet $1$ et $- 1$ comme valeurs d'adhérence. En effet, les termes pairs sont constants à $1$ et les termes impairs constants à $- 1$ .

la suite $(sin(n))$ admet l'intervalle $[ - 1,1]$ comme ensemble de valeurs d'adhérence. Ceci résulte du fait que $\mathbb{Z}+ 2\pi\mathbb{Z}$ est dense dans $\mathbb{R}$ .

la suite $(( - 1) n n)$ n'admet pas de valeur d'adhérence. Mais dans la droite réelle achevée, la même suite admet 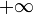$+\infty$ et $-\infty$ comme valeurs d'adhérence.

la suite $(( - 1) n n + n)$ admet 0 comme unique valeur d'adhérence mais ne converge pas. Dans la droite réelle achevée, la même suite admet 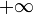$+\infty$ et 0 comme valeurs d'adhérence.

L'ensemble des valeurs d'adhérence

Les exemples ci-dessus montrent que l'ensemble des valeurs d'adhérence d'une suite réelle peut avoir 0, plusieurs éléments ou une infinité d'éléments. Du point de vue topologique, on peut montrer que cet ensemble est toujours fermé. En effet en inversant les deux quantificateurs dans la propriété si 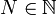$N\in\mathbb{N}$ , la propriété $(\forall \varepsilon\in\mathbb{R}, \;\varepsilon >0)(\exist n>N, \;|u_n-a|<\varepsilon)$

signifie exactement que $a$ est dans l'adhérence de $\left\{u_n,\;n>N\right\}$ que l'on note $\overline{\left\{u_n,\;n>N\right\}}$ . La reformulation ensembliste de la dernière propriété est donc, si l'on note $U$ l'ensemble des valeurs d'adhérence de la suite :

$U=\bigcap_{N\in\mathbb{N}}\overline{\left\{u_n,\;n>N\right\}}$

Ce qui montre que $U$ est fermé comme intersection de fermés.

Définition générale

Soient $E$ un espace topologique, 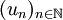$(u_n)_{n\in\mathbb{N}}$ une suite d'éléments de $E$ et $a$ un élément de $E$ . On dit que a est une valeur d'adhérence de la suite $(u n)$ si tout voisinage de $a$ possède une infinité de termes de la suite. $a$ est alors dans l'adhérence de l'ensemble $\{u_n, n\in\mathbb{N}\}$ . Intuitivement, la suite repasse aussi près que l'on veut de la valeur d'adhérence pour des indices arbitrairement grands.

Il suffit pour cela qu'il existe une Sous-suite de $(u n)$ qui converge vers $a$ . Cette dernière condition est équivalente à la définition si tout point de $E$ admet une base dénombrable de voisinages. C'est le cas par exemple des espaces métriques.

Plus généralement, si $f$ est une fonction d'un espace topologique $E$ dans un espace topologique $F$ , on dit que $y$ est une valeur d'adhérence de $f$ en un point $x$ de $E$ si $y$ est adhérent aux images par $f$ de tous les voisinages de $x$ .

Exemples

Considérons l'ensemble E égal à la réunion de $\N \times \N$ et d'un singleton ${ω}$ . Munissons E de la topologie séparée suivante. Les points $(n, m)$ de $\N \times \N$ sont isolés et les voisinages de ${ω}$ sont les parties U de E contenant ${ω}$ et vérifiant la condition :

il existe

N

tel que, pour tout

n

supérieur ou égal à

N

, U contient tous les points de $\{n\} \times \N$ sauf un nombre fini.

Considérons la suite parcourant $\N \times \N$ par diagonales descendantes successives.

u 0 = (0,0)

u 1 = (1,0)

u 2 = (0,1)

u 3 = (2,0)

u 4 = (1,1)

u 5 = (0,2)

, etc... Alors cette suite admet

{ω}

comme valeur d'adhérence, mais aucune sous-suite ne converge vers

{ω}

^[1].

dans $\R$ la fonction $x \to \sin(1/x)$ admet $[ - 1,1]$ comme ensemble des valeurs d'adhérence de la fonction en 0.

Propriétés

Voir aussi

Notes et références

↑ James Dugundji, Topology, Wm. C. Brown Publishers (1989), p.214-215

Portail des mathématiques

Ce document provient de « Valeur d%27adh%C3%A9rence ».

Catégories : Suite | Topologie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Valeur d'adherence de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Valeur d'adhérence — Pour les articles homonymes, voir Adhérence. En topologie, si est une suite à valeurs dans un ensemble E, une valeur d adhérence de la suite (un) est un point de E près duquel s accumulent une infinité de termes de la suite. Pour donner un sens… … Wikipédia en Français
adhérence — [ aderɑ̃s ] n. f. • XIVe; bas lat. adhaerentia 1 ♦ État d une chose qui adhère, tient fortement à une autre. L adhérence des pneus au sol. ♢ Méd. Union accidentelle ou pathologique de tissus contigus, dans l organisme. Adhérence pleurale. Au plur … Encyclopédie Universelle
Adherence (mathematiques) — Adhérence (mathématiques) Pour les articles homonymes, voir Adhérence. En topologie, l adhérence d une partie d un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la… … Wikipédia en Français
Adhérence (Mathématiques) — Pour les articles homonymes, voir Adhérence. En topologie, l adhérence d une partie d un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la convergence de suites dans les… … Wikipédia en Français
Adherence — Adhérence Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Adhérence (mathématiques) — Pour les articles homonymes, voir Adhérence. En topologie, l adhérence d une partie d un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la convergence de suites dans les… … Wikipédia en Français
Adhérence — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « adhérence », sur le Wiktionnaire (dictionnaire universel) Physique L’adhérence est un phénomène qui… … Wikipédia en Français
Valeur — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Valeur », sur le Wiktionnaire (dictionnaire universel) Le mot « valeur », du latin classique … Wikipédia en Français
Adherence (physique) — Adhérence (physique) Pour les articles homonymes, voir Adhérence. Préchauffage d un pneumatique de motocyclette pour diminuer sa dureté et augmenter son adhérence, avant une … Wikipédia en Français
Adhérence (Physique) — Pour les articles homonymes, voir Adhérence. Préchauffage d un pneumatique de motocyclette pour diminuer sa dureté et augmenter son adhérence, avant une … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Valeur d'adherence

Valeur d'adhérence

Sommaire